Daniel Justens [1]

L’actuariat recouvre l’ensemble des méthodes mathématiques utilisées dans le monde des assurances. On parle d’actuariat de « premier type » ou encore d’actuariat « vie » lorsque l’on traite d’assurances couvrant le risque de décès ou de survie d’un assuré, d’actuariat de « deuxième type » pour qualifier tous les contrats couvrant des risques accidentels et, depuis quatre décennies, d’actuariat de « troisième type » pour tous les modèles financiers, lesquels se taillent aujourd’hui la part du lion étant donné l’importance et le nombre de produits étranges (on dit « exotiques ») qui inondent les marchés. Ces mathématiques ne sont pas avares d’utilisations du calcul matriciel. En voici quelques exemples.

1. Actuariat vie

Les contrats d’assurances « vie  » sont de deux types  : certains garantissent le paiement d’un capital déterminé en cas de survie d’un assuré à un âge donné (on parle alors de « capital différé »), d’autres le paiement de ce capital aux ayants droit au moment du décès de l’assuré (c’est l’assurance « décès »). Le contexte de ces contrats est donc celui d’un système à deux états : vie ou mort. L’assuré vivant peut rester vivant ou passer à l’état de « décédé  ». N’insistons pas trop sur l’unique possibilité de l’assuré mort. On peut convenir d’observer un assuré lors de ses anniversaires successifs et de noter systématiquement son état. Admettons que l’on puisse déterminer la probabilité p (0 < p < 1) de survie d’un assuré pendant un an, que nous supposons dans un premier temps indépendante de son âge. On note aussi q la probabilité de décès avec évidemment \(q = 1-p\). On peut alors noter les probabilités de transition d’états « vie/mort » au moyen de la matrice :

$$M=\begin{pmatrix} p & 1-p \\ 0 & 1 \end{pmatrix}$$

La première ligne décrit les probabilités de transition vers les deux états vie et mort d’un individu vivant. La deuxième ligne correspond aux probabilités de transition à partir de l’état « décédé  ». Cet état est qualifié d’absorbant pour des raisons évidentes dans notre contexte. On peut à présent s’intéresser à l’état de l’assuré après deux ans. En supposant les transitions successives indépendantes, on sait que la probabilité de survie après deux ans doit valoir \(p^2\) . La probabilité de décès étant complémentaire, doit être égale à \(1-p^2\) . En effet, ce décès a pu survenir pendant la première année (probabilité \(1 - p\)), ou durant la seconde, auquel cas l’assuré a du survivre un an puis décéder l’année suivante. Ces événements étant indépendants par hypothèse, leur probabilité de réalisation simultanée est égale au produit des probabités soit \(p.(1 - p)\). Les deux événements (décès la première ou la deuxième année) étant disjoints, la probabilité de réalisation de l’un ou l’autre des événements est égale à la somme des probabilités, soit \([1 - p] + [p(1 - p)] = 1 - p^2\) . On a vérifié ainsi que la matrice de transition d’états en deux ans correspondait exactement à la matrice \(M^2\) et donc que la procédure de calcul mise en place était exactement celle du produit matriciel. Avec :

$$M^2=\begin{pmatrix} p^2 & 1-p^2 \\ 0 & 1 \end{pmatrix}$$

On généralise sans peine ce résultat pour obtenir la matrice de transition d’états après n années :

$$M^n=\begin{pmatrix} p^n & 1-p^n \\ 0 & 1 \end{pmatrix}$$

On constate hélas que la limite pour n tendant vers l’infini de cette matrice prend la forme

$$M^\infty=\begin{pmatrix} 0 & 1 \\ 0 & 1 \end{pmatrix}$$

qui exprime que le seul état final atteignable, quel que soit l’état initial est celui de « décédé ». Apparaît ici la notion très claire d’état transitoire (être vivant) et d’état persistant (être mort). Toutes ces notions sont formalisées dans le cadre de la théorie des chaînes de Markov.

La réalité est différente et beaucoup plus complexe : les probabilités de transitions dépendent de l’état du système. Les probabilités de survie varient avec l’âge. On s’attend à en observer des valeurs en suite décroissante, la probabilité de décès des personnes plus âgées devant « naturellement » être supérieure. Ce n’est pas le cas :
les probabilités de décès des enfants de moins d’un an est significativement supérieure à celle des enfants de 2 à 10 ans. Vient ensuite une curieuse « bosse », attribuée aux accidents de la route et aux suicides et qui frappe surtout les jeunes hommes entre 15 et 25 ans. Car les probabilités de survie dépendent aussi du sexe de l’assuré. Ces résultats sont présentés sur le graphique suivant, donné en coordonnées semi-logarithmiques pour prendre en considération des valeurs d’ordres de grandeur significativement différents : de quelques pour-dix-mille à une dizaine de pour-cent.
Les abscisses donnent les âges et les ordonnées les probabilités observées de décès \(1 - p\) généralement notées \(q\) :

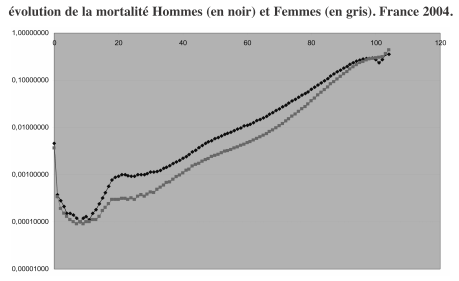
En notant \(p_x\) les probabilités de survie des hommes d’âge x et \(p’_x\) celles des femmes de même âge, nos matrices décrivant les probabilités de transition deviennent :

$$M_x=\begin{pmatrix} p_x & 1-p_x \\ 0 & 1 \end{pmatrix}$$

$$M’_x=\begin{pmatrix} p’_x & 1-p’_x \\ 0 & 1 \end{pmatrix}$$

où x désigne l’âge de l’assuré. L’interprétation des différentes valeurs de ces matrices est identique à celle qui a été proposée plus haut, à ceci près que les probabilités sont devenues conditionnelles : elles dépendent de l’âge (x) et du sexe (p ou p’). Après deux ans, on retrouve comme plus haut la multiplication matricielle classique :

$$M_xM_{x+1}=\begin{pmatrix} p_x & 1-p_x \\ 0 & 1 \end{pmatrix} \begin{pmatrix} p_x & 1-p_{x+1} \\ 0 & 1 \end{pmatrix}=\begin{pmatrix} p_x p_{x+1} & 1-p_x p_{x+1} \\ 0 & 1 \end{pmatrix}$$

Comme plus haut, la multiplication des matrices conditionnelles donne les probabilités de survie et de décès après deux ans, On retrouve, hélas !, les mêmes conclusions sinistres à long terme, à savoir l’existence d’un état transitoire (vie) et d’un autre persistant (mort).

Tournons-nous à présent vers les contrats couvrant les cas de maladie et/ou d’invalidité. Dans ce contexte, les choses sont un peu plus complexes puisque le système étudié (l’assuré) peut connaître 4 états  : être vivant et actif, vivant et invalide, mort en tant qu’actif ou mort en tant qu’invalide. Les deux derniers états sont considérés comme différents, les prestations de l’assureur étant le plus souvent significativement supérieures dans le second cas de figure, qui survient après deux changements d’état et se traduit donc généralement par deux débours de la part de l’organisme assureur. Reprenons une description des probabilités de transition d’état indépendante de l’âge comme plus haut :

$$M_x=\begin{pmatrix} p^{aa} & p^{ai} & q^{aa} & q^{ai} \\ p^{ia} & p^{ii} & q^{ia} & q^{ii} \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix}$$

Les exposants a et i font référence à l’état initial (premier indice) et final (second indice) de l’assuré, a signifiant actif et i, invalide. Les notations p se réfèrent au maintien dans l’état de vivant, les notations q quantifient comme plus haut les probabilités de passage à l’état de décédé. Ainsi la notation \(p_x^{aa}\) correspond elle à la probabilité de survie pendant un an d’un actif d’âge x tout en demeurant actif et \(p_x^{ai}\) à celle de survie d’un actif mais devenant invalide pendant la même période. Les autres probabilités obéissent aux mêmes notations. Les sommes des éléments de chaque ligne doivent évidemment être égales à 1. Pour simplifier un peu cette matrice, les assureurs font généralement l’hypothèse de non retour à l’état d’activité
en partant de l’état d’invalide. Cette hypothèse est réaliste  : le passage à l’état d’invalide se traduit généralement par le versement d’un capital. On imagine mal une compagnie d’assurances exigeant la restitution de ce capital en cas de guérison miraculeuse. Voici la matrice simplifiée avec suppression des doubles indices inutiles :

$$M_x=\begin{pmatrix} p^{aa} & p^{ai} & q^{aa} & q^{ai} \\ 0 & p^{ii} & 0 & q^{ii} \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix}$$

Pour traduire cette hypothèse selon la terminologie des chaînes de Markov, on dit que l’ensemble des états d’invalidité est un ensemble fermé.

On doit alors particulariser toutes ces probabilités de transition en fonction de l’âge et du sexe des assurés. Par matrice, donc par catégorie d’âge et de sexe, on doit calibrer 6 paramètres. Ces paramètres sont liés  : les transitions d’états sont des distributions de probabilité pour lesquelles les sommes de probabilités doivent être égales à 1. Restent 4 degrés de liberté par matrice. En considérant des catégories d’âge de 0 à 104 ans, ce sont 840 paramètres que les assureurs sont censés estimer !
On constate ici à quel point le processus de tarification de ce type de contrat est délicat.

Signalons que le passage des probabilités de transition aux tables de tarification ne se fait pas sans difficulté : pour des raisons techniques, il n’est pas possible de tarifer immédiatement à partir des observations et une modélisation parfois délicate doit être proposée et calibrée. Les contrats d’assurances vie et d’assurances dépendances font l’objet de recherches en cours visant à proposer des modèles projectifs intégrant l’évolution des populations concernées. Les probabilités sont alors triplement conditionnelles : relativement au sexe, à l’âge et au moment du calcul.

2. Actuariat accident

Nous sommes presque tous conducteurs et par conséquent presque tous confrontés à l’obligation de souscrire une assurance responsabilité civile. Celle-ci est tarifée à partir d’échelles de primes calculées selon deux modes complémentaires : le mode a priori, en fonctions de critères plus ou moins arbitraires, et a posteriori, en fonction du comportement de chaque conducteur. Parmi les critères a priori, on retiendra par exemple le type de véhicule et sa puissance, l’âge du conducteur, son lieu de résidence, sa profession, la date d’émission de son permis de conduire. Le critère a posteriori paraît plus objectif puisqu’il consiste à observer le comportement de l’assuré en comptabilisant chaque année le nombre d’accidents en tort à mettre à son crédit (ou à son débit ?). Notons que le nombre d’accidents en droit pourrait également être pris en compte, ce renseignement apportant énormément d’informations sur le comportement du conducteur…

Sur base des critères a priori l’organisme assureur détermine une première prime qui pourra éventuellement soit augmenter l’année suivante si l’assuré est responsable d’accidents, soit diminuer s’il n’est responsable d’aucun. L’assureur doit établir une échelle de tarification définissant différents niveaux de primes notés de 0 à s. Le niveau d’entrée dans le système, q (0 < q < s), doit aussi être déterminé. Ces niveaux représentent les états du système. Des règles de passage d’un niveau de tarification à l’autre doivent être définies par l’organisme assureur. Les probabilités de passage d’un état à l’autre sont présentées dans une matrice que l’on construit à partir des règles de passage et des probabilités \(p_k\) d’observer k accidents dans l’année qui vient.

Supposons pour simplifier que le système compte 5 états correspondant à 5 niveaux de prime croissants, notés \(E_0, E_1, E_2, E_3, E_4\) et que chaque accident en tort provoque le passage dans le niveau de tarification supérieur alors que l’absence d’accident permet de redescendre d’un cran. Sous ces conditions simplifiées pour l’exemple (les systèmes réels comportent plus d’états et des règles de transition plus complexes), la matrice de probabilités de transition prend la forme suivante (la dernière colonne est construite pour obtenir une distribution de probabilité à chaque ligne) :

$$M_x=\begin{pmatrix} p_0 & p_1 & p_2 & p_3 & 1-p_0- p_1-p_2-p_3 \\ p_0 & 0 & p_1 & p_2 & 1-p_0- p_1-p_2\\ 0& p_0 & 0 & p_1 & 1-p_0- p_1\\ 0&0 & 0 & p_0 & 1-p_0 \end{pmatrix}$$

La première ligne donne les probabilités de transition à partir de l’état initial \(E_0\), et correspond successivement, étant données nos règles de transition, à la probabilité de ne pas être responsable d’accident (maintien), à celle d’en avoir causé un (transition vers l’état \(E_1\)) deux, ou trois, jusqu’à la dernière colonne correspondant à la probabilité d’être responsable de plus de 3 accidents. Les lignes qui suivent s’interprètent de la même façon. La modélisation des probabilités d’accident se fait habituellement au moyen d’une distribution de Poisson de paramètre \(\lambda\) qui quantifie le nombre moyen d’accidents dont l’assuré est responsable chaque année. Le problème consiste à affecter à chaque assuré le bon \(\lambda\). Pour arriver à une tarification sur base d’observations issues d’un portefeuille hétérogène, les actuaires considèrent généralement ce paramètre comme une deuxième variable aléatoire. Ceci donne naissance à ce que l’on nomme les distributions Poisson mélange.

Regardons comment évolue un portefeuille de clients pour lequel les fréquences d’assurés présents dans les 5 états ou niveaux de prime sont représentées par le vecteur \(A = (a_0, a_1, a_2, a_3, a_4)\) avec \(a_0+ a_1+ a_2+ a_3+ a_4= 1\).

Après un an, la compagnie d’assurance se trouvera en présence d’un portefeuille caractérisé par un vecteur de fréquences AP. Après deux ans, ce vecteur sera \(AP^2\) et, après n années \(AP^n\) .

Chaque compagnie peut ainsi déterminer le niveau total de ses encaissements étant donné les primes initiales et la grille de taux de primes choisie. Ceci est fondamental pour une gestion réaliste, l’idéal étant évidemment la constitution d’un portefeuille rentable et stable.

Pour obtenir un tel portefeuille stable, de composante \(B = (b_0, b_1, b_2, b_3, b_4)\), ne changeant pas au niveau des perceptions de primes, année après année, on doit avoir B = BP. Un tel portefeuille de composante B est appelé distribution stationnaire.
_Sous certaines conditions, on peut démontrer que tout portefeuille tend naturellement vers cette distribution stationnaire, ou encore que

$$\lim_{n \to \infty} AP^n=B$$

ce qui malheureusement ne garantit aucunement la rentabilité de ce secteur d’activité d’assurances.

3. Actuariat financier

Venons-en au dernier né de la famille actuarielle, reprenant les modélisations mathématiques des actifs financiers inondant actuellement les marchés. Ces actifs étaient constitués au départ de titres financiers comme les obligations, et d’actions représentant les parts d’une entreprise en activité. Le marché s’est complété en émettant des produits plus complexes concrétisant des droits d’achat ou de vente d’actions ou de paniers d’actions, mais également de devises étrangères ou de taux d’intérêt, le tout éventuellement sous conditions diverses. Contentons-nous d’un portefeuille élémentaire constitué de k actions. Observons ce portefeuille pendant n jours. Comment allons-nous collecter l’information pratiquement ?

Notons \(X_1, X_2, … , X_k\) les variables représentant les « états  » des k actions du portefeuille, ou encore leur niveau de cotation. Chaque jour, on peut noter la cote de clôture de chaque action. On collecte ainsi quotidiennement un vecteur de valeurs associé à \((X_1, X_2, … , X_k)\). Afin de particulariser chaque observation du vecteur, on va utiliser une notation doublement indicée. Par convention, le premier indice sera
relatif à la variable, le second au numéro du jour d’observation, qui sera dans ce cas notre unité statistique. Comme les observations sont notées quotidiennement, lignes par lignes, chaque ligne correspondant aux valeurs associées pour chaque variable à un jour donné, l’ordre des indices sera naturellement « colonne-ligne » : la valeur \(x_ij\), sera donc située à la ligne j de la colonne i et représentera la j-éme observation de la variable \(X_i\). On se trouve donc à l’opposé de la notation matricielle usuelle utilisant l’ordre « ligne - colonne ». Une complication de plus dans cet univers mathématique déjà plus que sophistiqué !

L’utilisation de tableaux de ce genre en finance, notamment pour le calibrage de produits financiers, est loin d’être trivial. Des hypothèses non nécessairement vérifiées expérimentalement doivent être faites comme la normalité des taux de rendement observés ou encore la stationnarité des mouvements non prévisibles des actifs formant ce que l’on nomme leur « volatilité ». Malgré ces problèmes, nous voyons quotidiennement que nos marchés fonctionnent…

Bibliographie

Natacha Brouhns & Michel Denuit : Risque de longévité et rentes viagères : tables de mortalité prospectives pour la population assurée et évaluation du coût de l’anti-sélection. http://www.belgianactuarialbulletin.be/articles/vol02/05-Brouhns.pdf

Justens, Daniel – Hulin, Laurence (2003) : Théories actuarielles, (392 pages) éditions du Céfal, iSBN 287130136-0. Cet ouvrage est en consultation sur http://books.google.be/books

<redacteur|auteur=500>