Exercices :

Exercice 466-1 (Christian Planchon – Marvejols)

L’ivrogne

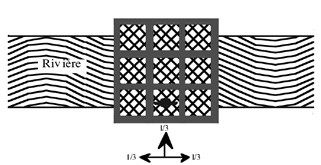
Pour rentrer chez lui, Don Garcia doit
traverser un pont sans balustrade,
constitué de trois rangées de trois dalles ;
ses amis l’ont laissé sur la dalle centrale
de la première rangée. Saoul comme il est,
s’il tombe à l’eau, c’est la noyade assurée.
Les yeux rivés sur l’autre berge, il
s’élance. Titubant, il a autant de chance de
faire un écart à gauche qu’un écart à droite
ou qu’un pas en avant.
L’amplitude de ses écarts et de ses pas étant égale aux côtés des dalles carrées, quelle
est la probabilité pour qu’il traverse ?

voir l’article où est publiée la solution

Exercice 466-2 (Stéphan Manganelli – Carpentras)

Les nombres métaux$$

Enseignant en TS, j’ai découvert (tout seul !) en début d’année, lorsque l’on
pratiquait, avec mes élèves, le théorème des fonctions continues strictement
monotones (bijections) pour résoudre par approche numérique (dichotomie,
balayage) certaines équations, le résultat suivant que je vous propose :
On connaît très bien le nombre d’or, solution positive de l’équation $x^2 = x + 1$.

On connaît un peu moins le nombre d’argent, solution de $x^3 = x^2 + x + 1$.

On connaît très peu le nombre de bronze, solution positive de $x^4 = x^3 + x^2 + x + 1.$

Et je m’arrête là pour la suite de ces nombres métaux … dont j’ai conjecturé et montré la convergence vers 2 ! (ce n’est pas très dur, les outils de terminale
suffisent).

voir l’article où est publiée la solution

Solutions

Exercice 461-4 (proposé par Gérard Macombe, IPR à Rennes).

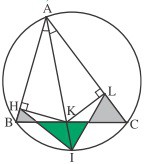
ABC est un triangle inscrit dans un cercle. La
bissectrice de l’angle $\widehat{BAC}$ coupe le cercle en I et [BC] en K. H et L sont les projetés orthogonaux de K sur (AB) et (AC).
Comparer l’aire du triangle vert à la somme des aires
des deux triangles gris.

Miguel Amengual Covas nous signale que c’est le
problème n°2 de la 28ème olympiade internationale de
mathématiques à Cuba en 1987.

Cet exercice a fait l’objet de réponses nombreuses et variées. Il fait donc aussi l’objet d’une présentation un peu plus longue qu’à l’habitude dans cette rubrique.

Solution de Richard Beczkowski (Dijon)
Solution de Michel Tanguy (Quimper)
Solution de Gérard Macombe (Rennes)

Une belle solution de Mireille Bournaud (Vitry-Sur-Seine) a donné lieu à une animation réalisée par François Colmez (Antony) que vous pouvez voir sur le site de l’APMEP.

Une autre solution de Bruno Alaplantive (St Jean du Falga) est également présentée sous la forme d’une animation que vous pouvez aussi voir sur le site de l’APMEP.

Autres solutions de Georges Lion (Wallis), Raymond Raynaud (Digne), Christian Planchon (Marvejols), Pascal Bray, et une solution graphique de Nicolas Patrois avec un logiciel de géométrie dynamique.