503
Exercices de-ci de-là du BV 503 et solutions des 501-1, 501-2, 501-3, 501-4
Exercices
Exercice 503-1 Daniel Reisz-Auxerre
\(2^\left[ {(5/2)^{2/5}} \right]\) n’est certes pas égal à e, mais … il s’en faut de moins d’un cent millième
comme le montre le logiciel Maxima :

Est-ce là pur hasard ou y a-t-il une explication ?.
voir l’article où est publiée la solution
Exercice 503-2 proposé par l’équipeMayhem de la revue canadienne Crux Mathematicarum
Dans le plan rapporté à un repère orthonormal, on considère l’ensemble \(\mathcal E\) des points
de coordonnées (x ; y) qui vérifient
$$x^2+y^2-22x-4y+100=0$$
Soit P un point de \(\mathcal E\) pour lequel le rapport \(\frac{y}{x}\) est le plus grand.
Montrer l’unicité de P et déterminer sa distance à l’origine.
voir l’article où est publiée la solution
Exercice 503-3 Jean Théocliste – Valence à proposer à nos élèves
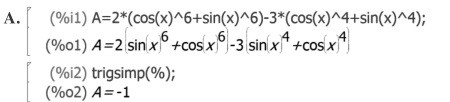
Prouver de deux façons le résultat ci-dessus, obtenu à l’aide d’un logiciel de calcul
formel, dans lequel x désigne un réel quelconque :
1) En considérant la fonction \(f : x \mapsto 2 \left( (\cos x)^6+(\sin x)^6 \right)-3 \left( (\cos x)^4+(\sin x)^4 \right)\)
définie pour tout réel x.
2) Par un autre moyen.
B. Divergence de la série harmonique
Montrer que pour tout entier naturel n (n ≥ 2), on a
$$\frac{1}{n-1} + \frac{1}{n} + \frac{1}{n+1} >\frac{3}{n}$$
Une preuve de la divergence de la série harmonique commence par
$$1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+\frac{1}{6}+\frac{1}{7}+\frac{1}{8}+\frac{1}{9}+\frac{1}{10}+....$$
$$= 1+\left( \frac{1}{2}+\frac{1}{3}+\frac{1}{4}\right)+\left(\frac{1}{5}+\frac{1}{6}+\frac{1}{7}\right)+\left(\frac{1}{8}+\frac{1}{9}+\frac{1}{10}\right)+....$$
etc. Terminer la démonstration.
voir l’article où est publiée la solution
Exercice 503-4 Paul Aubert – Paris
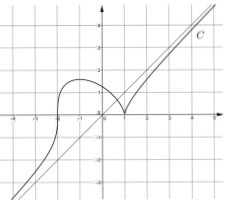
Sur la figure ci-contre, C est la courbe
représentative d’une fonction définie par une
seule et même formule sur tout l’ensemble \(\mathbb R\) .
On peut tenir pour exacts les renseignements
que l’on peut lire sur le graphique.
Trouver l’expression de la fonction.
voir l’article où est publiée la solution
Solutions
Exercice 501-1 Michel Lafond-Dijon
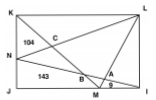
Le rectangle IJKL est partagé en huit domaines.
(Voir figure approximative ci-contre)
On connaît :
aire (CNK) = 104,
aire (AMI) = 9 et
aire (BMJN) = 143
Déterminer les aires des cinq autres domaines.
Solutions : Pierre Renfer (Saint Georges d’Orques), Michel Lafond (Dijon), Marie-Nicole Gras(Bourg d’Oisans)
Voir la solution de Marie-Nicole Gras.
Remarque. Michel Lafond et Pierre Renfer ont tous les deux utilisé une application
affine qui multiplie la largeur du rectangle par une constante k et divise la longueur
du rectangle par la même constante k permettant ainsi de transformer le rectangle en
un carré tout en conservant les aires.
Exercice 501-2 Daniel Reisz – Auxerre à proposer à nos élèves
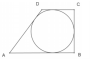
A. Un trapèze ABCD est circonscrit à un cercle de rayon 2 cm
comme le montre la figure ci-contre.
Le côté [CD] mesure 3 cm et les angles en B et C sont
droits.
Calculer l’aire de ABCD.
B. Si les angles d’un triangle ABC sont en progression arithmétique et les côtés en progression géométrique, montrer qu’il est alors équilatéral.
C. Montrer que sur \(\left] 0 ; \frac {\pi} {2} \right[\), on a \(sin(\sqrt x)<\sqrt{sin(x)}\)
Solutions : Pierre Renfer (Saint Georges d’Orques), Jean Gounon (Chardonnay), Daniel Reisz(Auxerre).
Exercice 501-3 (Jean Théocliste – Valence)
Calculer la valeur exacte de l’intégrale \(\int_{- \frac{\pi}{2}}^0\frac{(cos\ x)^2+1}{1-sin\ x} dx\) .
Solutions : Jean Théocliste (Valence), Pierre Renfer (Saint Georges d’Orques), Jean Gounon (Chardonnay), Michel Sarrouy (Mende).
Voici la solution de Jean Théocliste.
Exercice 501-4 pioché dans les 36èmes olympiades mathématiques espagnoles
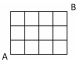
Sur le réseau quadrillé ci-contre formé de 12 carrés, une personne
P se déplace de A à B ; une personne Q, de B à A. Elles partent au
même instant et vont à la même vitesse en suivant un trajet le plus
court possible. À chaque intersection elles choisissent entre les
chemins possibles avec une même probabilité.
Quelle est la probabilité que P et Q se croisent en chemin ?
Solution : Michel Lafond (Dijon).
<redacteur|auteur=500>































