Exercices

Exercice 505 - 1 Jean-Yves Hély – Rennes issu du
Baccalauréat séries scientifiques, Lyon 19.. ( ?)

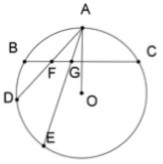
_ Étant donné sur une circonférence dont le centre est
O, un arc BC, du milieu A de cet arc, on mène les
deux autres sécantes AFD et AGE.

Démontrer que l’on a
\(FE \times DG = DF \times GE + FG \times DE.\)

voir l’article où est publiée une solution

Exercice 505 - 2 Jean-Pierre Friedelmeyer – Strasbourg
Trouver toutes les paires de fractions \(\left\{ \frac{p}{q}, \frac{r}{s} \right\}\), avec p, q, r, s entiers naturels non nuls,
telles que \( \frac{p}{q} \times \frac{r}{s} = \frac{p}{q} + \frac{r}{s}\)

voir l’article où est publiée une solution

Exercice 505 - 3 Raymond Heitz – Piriac
On donne dans le plan une droite (D) et deux points A et B situés hors de (D) du même côté de (D). Construire un cercle passant par A et B et découpant sur (D) un segment de longueur donnée.

voir l’article où est publiée une solution

Exercice 505 - 4 Noel Ard – Pise

La suite \(v_n\) est définie pour tout entier naturel non nul par

$$v_n=u_n \times 10^{-n-1}$$

où \(u_n\) désigne le n-ième terme de la suite de Fibonacci.

Prouver que la somme des termes de \((v_n)\) est égale à \(\frac{1}{89}\).

voir l’article où est publiée une solution

Solutions

Exercice 503-1 Daniel Reisz-Auxerre
\(2^\left[ {(5/2)^{2/5}} \right]\) n’est certes pas égal à e, mais … il s’en faut de moins d’un cent millième
comme le montre le logiciel Maxima :

Est-ce là pur hasard ou y a-t-il une explication ?.

Solutions : Jean-Yves Hély (Rennes), Daniel Reisz (Auxerre)
Voici la solution de Jean-Yves Hély.

Remarque. L’équation \(2^\left[ {x^{\left (\frac{1}{x}\right)}} \right]=e\) n’admet pas de solution d’ordre algébrique. C’est
ce qui motive l’étude de la fonction f.

Exercice 503-2 proposé par l’équipeMayhem de la revue canadienne Crux Mathematicarum
Dans le plan rapporté à un repère orthonormal, on considère l’ensemble \(\mathcal E\) des points
de coordonnées (x ; y) qui vérifient

$$x^2+y^2-22x-4y+100=0$$

Soit P un point de \(\mathcal E\) pour lequel le rapport \(\frac{y}{x}\) est le plus grand.
Montrer l’unicité de P et déterminer sa distance à l’origine.

Solutions : Pierre Renfer (Saint Georges d’Orques), Jean Gounon (Chardonnay),
Michèle Malléus ( Châtenay-Malabry), Raymond Heitz (Piriac), Georges Lion
(Wallis), Jean-Yves Hély (Rennes).
Voici la solution de Michèle Malléus.

Remarque. Michèle Malléus et Jean Gounon proposent également une solution analytique.

Exercice 503-3 Jean Théocliste – Valence à proposer à nos élèves

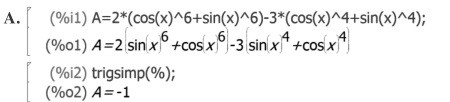
Prouver de deux façons le résultat ci-dessus, obtenu à l’aide d’un logiciel de calcul
formel, dans lequel x désigne un réel quelconque :
1) En considérant la fonction \(f : x \mapsto 2 \left( (\cos x)^6+(\sin x)^6 \right)-3 \left( (\cos x)^4+(\sin x)^4 \right)\)
définie pour tout réel x.
2) Par un autre moyen.

B. Divergence de la série harmonique
Montrer que pour tout entier naturel n (n ≥ 2), on a

$$\frac{1}{n-1} + \frac{1}{n} + \frac{1}{n+1} >\frac{3}{n}$$

Une preuve de la divergence de la série harmonique commence par

$$1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+\frac{1}{6}+\frac{1}{7}+\frac{1}{8}+\frac{1}{9}+\frac{1}{10}+....$$

$$= 1+\left( \frac{1}{2}+\frac{1}{3}+\frac{1}{4}\right)+\left(\frac{1}{5}+\frac{1}{6}+\frac{1}{7}\right)+\left(\frac{1}{8}+\frac{1}{9}+\frac{1}{10}\right)+....$$

etc. Terminer la démonstration.

Solutions : Pierre Renfer (Saint Georges d’Orques), Georges Lion (Wallis), Jean-Yves Hély (Rennes), Daniel Vacaru (Roumanie).

Nota. Ainsi que le mentionne Jean-Yves Hély, cette démonstration de la divergence
de la série harmonique est due au prêtre italien Pietro Mengoli vers 1650.

Exercice 503-4 Paul Aubert – Paris

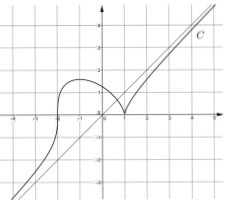
Sur la figure ci-contre, C est la courbe
représentative d’une fonction définie par une
seule et même formule sur tout l’ensemble \(\mathbb R\) .
On peut tenir pour exacts les renseignements
que l’on peut lire sur le graphique.
Trouver l’expression de la fonction.

Solutions : Georges Lion (Wallis), Georges Guenim (Roufiac), Michèle Malléus (Châtenay-Malabry), Raymond Heitz (Piriac), Jean-Yves Hély (Rennes).
Voici in extenso (!) la solution de Raymond Heitz.

Remarques. Effectivement, l’homonymie est forte !!! L’exemplaire du manuel édité chez Vuibert, à l’usage des élèves de Mathématiques Supérieures, de première année de Mathématiques Spéciales et des étudiants de Mathématiques Générales, que je détiens, est daté de 1948.
Je chipoterais bien en faisant remarquer que la courbe est en page 102, mais ce serait être mauvais joueur …

Georges Guenim, lui, me fait part de la présence du même exercice dans le Lebossé Hémery (Terminales C, D et T Programme 1966).

Pour Louis-Marie Bonneval, relecteur et correcteur des coquilles de la rubrique, cette
figure évoque, après rotation de 3/8 de tour dans le sens indirect, les courbes
voluptueuses chères à Pierre Gallais :
http://www.institutdemathologie.fr/

<redacteur|auteur=500>