Exercices

Exercice 510-1 Michel Lafond – Dijon arithmétique
n est un entier naturel positif écrit en base dix. On note d(n) le dernier chiffre de n et s(n) la somme des chiffres de n.

Si $a=\frac{3^{2014}-1}{2}$ démontrer que d(a) = s(s(s(a))).

voir l’article où est publiée une solution

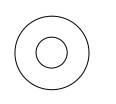
Exercice 510 - 2 Greg Leceul – Detroit only rule
Deux cercles concentriques étant donnés sans leur centre, retrouver
celui-ci à la règle seule (sans graduation).

voir l’article où est publiée une solution

Exercice 510 - 3 Louis-Marie Bonneval – Poitiers pour nos élèves
Les organisateurs du banquet disposent de tables rondes de 150 cm de diamètre. Ils ont fait faire des nappes carrées pour les recouvrir. Mais suite à une erreur de mesure ces nappes ne font que 140 cm de côté.
Peuvent-ils avec deux nappes recouvrir complètement une table ?

voir l’article où est publiée une solution

Exercice 510 - 4 Jean-Pierre Friedelmeyer – Osenbach
• Dans un plan euclidien, déterminer et construire à la règle et au compas les carrés dont les côtés (éventuellement prolongés) passent par quatre points donnés du plan.

Et le problème dual :
• Dans un plan euclidien, déterminer et construire à la règle et au compas les carrés dont les sommets sont situés sur quatre droites données du plan.

voir l’article où est publiée une solution

Solutions

Exercice 508-1 Jean-Pierre Friedelmeyer – Osenbach

Une lunule d’Hippocrate est délimitée par le demi-cercle de diamètre [AB] et le quart de cercle (OAB) de centre O.
On demande de partager cette lunule en n parties d’aires
égales, par des rayons issus de O.

Voici la solution de Pham Dang Long puis celle de André Stoll

Exercice 508–3 Georges Lion – Wallis tiré de « Euclid and beyond », par Robin Hartsborne
Soit un angle droit $\widehat{xOy}$, un point A à l’intérieur du premier quart de plan et un point B sur [Oy) tels que OB > OA.
Construire le cercle de centre O coupant [Ox) en C et [Oy) en D tels que les droites (BC) et (DA) soient parallèles.

Solutions : Pierre Lapôtre (Calais), Odile Simon (La Prénessaye), Raymond Heitz (Piriac), Georges Lion (Wallis).

Voici la solution de Odile Simon.

Remarque.
La contrainte OB > OA permet simplement de limiter les différents cas pour les
constructions, sans être spécifique de l’existence et de l’unicité de la solution.

Exercice 508–4 à défaut de se plier en quatre … pour nos élèves

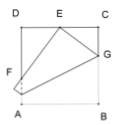
Voici un pliage, connu sous le nom de théorème de Haga, qui permet de déterminer le tiers du côté d’un carré.
Le milieu E du côté [DC] ayant été marqué au préalable (on ramène [CB] sur [DA] et on ne fait que marquer le pli sur E), on plie le carré ABCD de façon à amener le coin inférieur droit B, sur E.
Le côté qui était en bas coupe maintenant le côté gauche
[DA] en F.
Il s’agit de prouver que F est au tiers (ou aux deux tiers)
du côté [DA].
On peut faire plier des carrés de côté 8 ou 16 cm par exemple…

Solutions : Pierre Lapôtre (Calais), Pierre Renfer (Saint Georges d’Orques), Marie-Nicole Gras (Le Bourg d’Oisans), Raymond Heitz (Piriac), Odile Simon (La Prénessaye).

Voici la solution de Pierre Lapôtre (qui propose une première solution analytique, puis celle qui suit)

<redacteur|auteur=500>