par Patrick Guyot [1]

Oui, Julien, répondit le patron. On ne se figure
pas combien les moindres objets dont nous nous
servons ont coûté de travail et même de science ;
car les ingénieurs qui dirigent les ouvriers dans
ces usines ont dû faire de longues et pénibles
études, pour savoir se reconnaître au milieu dé
toutes ces inventions et de ces machines si
compliquées. Que serait la force de l’homme sans
la science ?

(Le Tour de la France par deux enfants,
Giordano BRUNO, Belin, 1877.)

L’une des premières décisions des frères Schneider lors de leur prise de
possession en 1837 de l’usine du Creusot (Saône-et-Loire) concerne la « création
d’une école primaire et d’une école supérieure pour les jeunes gens, appropriées aux
différentes industries de l’établissement, voulant témoigner aux ouvriers attachés à
leur établissement toute leur sollicitude pour leur bien-être et celui de leur famille »
(Citation d’Eugène Schneider).

L’entreprise a acquis son heure de gloire au XIXe siècle dans la fabrication de
locomotives, de canons, d’ouvrages importants à structure métallique ; elle comptait
alors parmi les trois ou quatre principales d’Europe.

Sans vouloir entrer dans une polémique stérile concernant ce type d’écoles ayant
existé pendant la deuxième moitié du XIXe siècle et la première moitié du XXe
siècle, on peut néanmoins relever quelques points importants dont découle l’esprit
qui y régnait.

À leur actif, il faut souligner que, pour l’époque, on se préoccupait de la culture
des ouvriers, en plus de leur accès à des logements décents et aux soins organisés,
qu’une promotion sociale était possible pour les bons élèves (les meilleurs issus de
familles pauvres pouvaient même devenir caboulotins et sortir ingénieurs-maison), et
enfin que l’école était peu ou pas payante, même pour les enfants de personnes ne
travaillant pas à l’usine.

Mais on doit également reconnaître que le paternalisme et l’endoctrinement
régnaient fortement, que la main-d’œuvre était attachée : l’emploi à l’usine était
pratiquement la seule solution pour les gens formés sur place (cadres-maison). De
plus, pour que les enfants soient aidés, il fallait que les parents fissent preuve de
bonne volonté et de leur esprit « Schneider ».

Un ouvrage datant de 1912 « Les
Établissements Schneider - Économie Sociale »
(Paris, Lahure, 1912) explique le fonctionnement de
la société au Creusot autour de l’onmiprésente usine.
Ce livre est un reflet de la pensée de la famille
Schneider. On y lit par exemple :
« L’instruction n’est pas obligatoire mais nul
enfant du Creusot n’est reçu à l’Usine s’il ne sait
lire.
A sa sortie de l’École, chaque élève est placé par
les chefs de l’Usine d’après ses notes, ses aptitudes
et ses succès, sans distinction de familles, sans autre
titre de préférence que les droits acquis à l’école.  »

La structure en degrés successifs des Écoles Schneider se présente selon le
schéma suivant :
 École élémentaire (enseignement primaire) : 4 degrés.
 Groupe spécial (enseignement primaire supérieur) : 4 degrés.
 Cours supérieur (le Caboulot) ; il conduit les meilleurs aux postes de contremaître
ou d’ingénieur : 3 degrés.

Des sorties sont possibles en cours d’étude et permettent aux élèves de devenir
élèves-ouvriers ou employés selon leurs résultats.

Qu’y enseigne-t-on ?
« La lecture, l’écriture, le calcul, puis un peu de grammaire, d’histoire, de
géographie sont enseignés à tous. Après, viennent la géométrie, le dessin linéaire,
qui sont dans l’usine d’une application continue et qu’il est, par conséquent,
indispensable de connaître. Dans cette situation, dans ces épreuves préliminaires,
des aptitudes spéciales, des sujets plus intelligents que les autres se révèlent. On
met immédiatement ceux-là en apprentissage dans les ateliers,. quelques uns sont
envoyés, aux frais du Creusot, dans des écoles spéciales, comme celles des Arts
et Métiers, et ils en reviennent tout prêts à faire un jour des contremaîtres
accomplis.
C’est par cette rigoureuse discipline donnée au corps et à l’esprit, que le
Creusot a assuré son recrutement. Il y a longtemps qu’on l’a dit : "C’est le maître
qui fait l’ouvrier. " »
(Louis Simonin, Le Creusot et les mines de Saône et Loire, 1865)

Nous pouvons souligner qu’à tous les échelons de l’entreprise, il était nécessaire
que le personnel fût formé à la réalisation et à la lecture de plans et de dessins.

Quels sont les contenus de programme ?

Pour les élèves de douze ou treize ans, le programme de mathématiques
comporte : arithmétique (les quatre opérations, système métrique, fractions, règle de
trois, intérêt, escompte, rentes, partages proportionnels, problèmes pratiques),
géométrie (les lignes, les angles, les polygones et la circonférence, les aires, les
volumes : surface latérale, surface totale et volume, problèmes pratiques), géométrie
descriptive (projection et perspective cavalière du point, de la ligne, des surfaces et
des volumes, perspective cavalière d’objets usuels), dessin graphique (tracé des
perpendiculaires, des parallèles, construction des angles, des triangles, des
parallélogrammes ; division de la circonférence, des arcs ; polygones inscrits et
circonscrits ; tracés de courbes usuelles ; outils de traçage, leur emploi, croquis cotés
d’objets usuels).

On ajoute ensuite pour le groupe spécial la trigonométrie (résolution des triangles
rectangles et cas principaux des triangles quelconques ; applications), l’algèbre
(pratique du calcul algébrique et de l’équation du premier degré à une et à deux
inconnues, théorie des quatre opérations, systèmes d’équations du premier degré,
calcul des radicaux, pratique de l’équation du second degré, division des polynômes,
inégalités, progressions, logarithmes, trinôme du second degré, maxima et minima,
représentation graphique des fonctions), la géométrie dans l’espace et des
compléments de géométrie descriptive (changements de plans, rotations,
rabattements, projection des surfaces, des polyèdres ; sections planes des polyèdres).

Enfin, pour les meilleurs élèves du groupe spécial qui entrent au cours supérieur,
l’enseignement scientifique et technique est d’un niveau élevé, se rapprochant de
celui de l’École Centrale des Arts et Manufactures ; on y étudie en mathématiques :
 Théorie des transversales, pôles et polaires, inversion, cercles tangents, géométrie
sphérique, coniques, hélices et spirales, cycloïdes.
 Arpentage et nivellement.
 Géométrie descriptive : polyèdres, cônes, cylindres, sphères, intersections.
 Trigonométrie : équations trigonométriques, topographie.
 Algèbre : analyse combinatoire, binôme de Newton, fonctions, logarithmes,
dérivées, primitives, déterminants, imaginaires, équations algébriques, différentielles,
développements en série, formes indéterminées, maxima et minima,
intégrales indéfinies, intégrales définies, méthodes d’intégration, intégrales doubles
et triples, séries entières, équations différentielles.
 Géométrie analytique : courbes du deuxième degré, géométrie analytique à trois
dimensions (quadriques).

La géométrie de Béché

Un ouvrage de géométrie qui eut son heure de gloire au début du siècle rend bien
compte de l’esprit animant cet enseignement. Il a été rédigé en quatre volumes (un
par année de l’enseignement primaire supérieur) par A. Béché en 1920 et publié aux
éditions Armand Colin. Nous pouvons relever les objectifs et les méthodes
privilégiés dans ce livre à travers quelques passages de la préface.

Cette préface insiste en premier lieu sur le niveau d’exigence : enseignement à but
pratique, soit, mais sans perdre de vue le rôle formateur de la géométrie.

« Si élémentaire et limité qu’il soit, le savoir de l’écolier doit être un savoir
sûr et précis : il importe que l’élève prenne de plus en plus conscience de la
certitude mathématique.
Pour être concret et pratique, l’enseignement de la Géométrie n’en doit pas
moins être celui qui convient à une science exacte. [ ..]
L’enseignement primaire supérieur, s’il vise à faire acquérir à l’élève des
connaissances pratiques nombreuses et variées, doit surtout avoir en vue le
développement des facultés de l’intelligence : c’est en quelque sorte
l’enseignement secondaire mis à la portée de tous ceux qui, en dépit de leurs
aptitudes, n’ont ni les moyens ni le temps de fréquenter le lycée ... »

L’auteur envisage ensuite le rôle du manuel en complément du cours du professeur.

«  À notre avis, le livre de Géométrie ne doit pas être la reproduction fidèle des
leçons du maître.
Dans une leçon, le professeur illustre son enseignement par de nombreux
exemples extraits des milieux familiers aux élèves et par des vérifications
expérimentales qu’il tire des enseignements connexes de celui de la Géométrie,
et, en particulier, des exercices de travaux manuels dont l’aide est des plus
efficaces.
Mais ce qui doit se dégager de cette leçon, c’est la démonstration de quelques
vérités géométriques, et c’est cela seulement que l’élève doit retrouver dans son
livre. Les exemples concrets auxquels le maître aura fait appel, l’écolier en aura
encore l’image devant les yeux, quand il étudiera sa leçon, et c’est pourquoi il est
inutile d’en encombrer le texte du livre ... ».

Des conseils sur les méthodes de travail à destination des professeurs ne sont pas
oubliés :

« On ne saurait trop appeler l’attention des maîtres sur la nécessité
d’analyser l’énoncé de tout théorème pour en distinguer l’hypothèse et la
conclusion. Il est indispensable d’exiger que l’élève, avant de démontrer un
théorème, écrive, en abrégé et dans une disposition choisie une fois pour toutes,
l’hypothèse et la conclusion.
Nous recommandons particulièrement le procédé qui consiste à écrire
l’hypothèse à gauche et la conclusion à droite de la figure. De cette manière,
l’élève peut, d’un coup d’oeil, recourir à l’une ou à l’autre, s’il craint de s’égarer
dans son raisonnement ...  ».

La place centrale accordée aux exercices et aux problèmes est soulignée à la fin de
la préface.

« La question des exercices et problèmes est primordiale en Géométrie. Outre
la gymnastique éminemment salutaire à laquelle ils soumettent l’initiative et le
raisonnement, des exercices nombreux et bien choisis permettent seuls, par
l’application répétée qu’ils en exigent, de fixer dans la mémoire les vérités
géométriques enseignées dans le cours. »

LE CREUZOT est ainsi appelé parce qu’il est situé dans le creux d’une vallée. Là s’est établie une des plus grandes usines de
l’Europe, dont on voit dans la gravure les cheminées fumer.
Autour de l’usine s’est bientôt groupée toute une population
d’ouvriers ; une ville s’est ainsi formée, qui compte maintenant
plus de 30000 habitants et s’accroit sans cesse.
(gravure extraite de Le Tour de la France par deux enfants,
G. Bruno, 1877, réédition Belin, 1977)

Monsieur Béché justifie le nombre très important de problèmes contenus dans
son ouvrage :

« Aussi est-il indispensable de faire le plus possible d’exercices et de
problèmes, tant en classe qu’en devoirs, et c’est pour cela que ce livre en contient
plus encore que n’en peuvent faire les élèves pendant la durée de leurs études,
afin de laisser au maître une marge pour le choix des exercices qu’il juge le plus
convenables au degré de force ou d’aptitude de ses élèves.
Parmi les exercices proposés, il en est qui sont des compléments
indispensables du cours et qui sont, en quelque sorte, obligatoires.  »

Nous pouvons nous rendre compte de ce que demande M. Béché par l’étude
d’exercices qu’il propose aux élèves de première année : il s’agit de la construction
d’un triangle rectangle à partir de la connaissance de deux de ses éléments.

L’examen de la série d’énoncés (207 à 218) reproduits ci-dessous montre la quasiexhaustivité
sur le sujet. ( Nous laissons au lecteur actif et attentif le soin de corriger
la coquille de l’énoncé 213). Les trois premiers exercices (207 à 209), précédés d’un
astérisque, sont considérés comme obligatoires, les suivants sont laissés à
l’appréciation du professeur.

 *207. Construire un triangle rectangle, connaissant l’hypoténuse a et un angle
aigu B.
 *208. l’hypoténuse a et un côté de l’angle droit b.
 *209. l’hypoténuse a et la hauteur h relative à l’hypoténuse.
 210. un côté de l’angle droit b et la hauteur h relative à l’hypoténuse.
 211. -la médiane m et la hauteur h relatives à 1’hypoténuse.
 212. l’hypoténuse a et le rayon r du cercle inscrit.
 213. un angle aigu B et le rayon r du cercle inscrit.
 214. un côté de l’angle droit b et le rayon r du cercle inscrit.
 215. l’hypoténuse a et la somme l des côtés de l’angle droit.
 216. l’hypoténuse a et la différence l des côtés de l’angle droit.
 217. un angle aigu B et la somme l des côtés de l’angle droit.
 218. un angle aigu B et la différence l des côtés de l’angle droit.

Le « livre du professeur »

Monsieur Béché a publié simultanément à ses ouvrages et chez le même éditeur
une sorte de livre du professeur qu’il a intitulé « Exercices corrigés » dans lequel il
développe ses conceptions (ou les conceptions en vigueur à l’époque) de résolutions
des problèmes. Ces résolutions ne sont plus tellement à la mode de nos jours car les
types de problèmes où on demande des constructions avec des contraintes ne se font
presque plus.

Le procédé qui intervient le plus souvent part du « problème résolu » et remonte
aux données de l’énoncé, comme nous pouvons le constater pour les corrigés des
exercices 208, 213, 215, et 218.

*208. Construire un triangle rectangle, connaissant l’hypoténuse a et un côté
de l’angle droit b.

S.

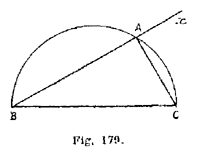
Supposons le problème résolu et soit ABC le triangle rectangle (fig,.179) dans lequel \(\hat{A }= 1 dr.\) BC =a ; CA=b.
On peut toujours construire l’hypoténuse BC = a.
Le problème revient alors à déterminer le sommet A.

1. Du point A, l’on voit BC sous un angle droit.
   Un lieu de A est donc la circonférence de diamètre
   BC.
2. 2° On a : CA = b. Un second lieu de A est donc la circonférence de centre C et de
   rayon b.
   A est à l’intersection des deux lieux. Il suffit ensuite de mener AB.
   La construction résulte immédiatement de ce qui précède.

Discussion. - Il faut que la circonférence (C,b) coupe la circonférence de diamètre
BC = a, ce qui exige : b < a.
Cette condition étant remplie, le problème a une solution.

213. - Construire un triangle rectangle, connaissant un angle aigu B et le rayon
r du cercle inscrit.
S. Supposons le problème résolu et soit ABC (fig 184) le triangle rectangle demandé.

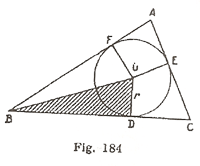
On peut construire le triangle rectangle
ODB dont on connait le côté OD = r ; l’angle \(\widehat{ODB} = 90\)° et l’angle \(\widehat{DOB}= 90-\frac{\hat{B}}{2}\)

Décrire ensuite le cercle (0, r), puis mener
la tangente BF et la tangente perpendiculaire
à BF. Pour cela, mener le rayon OE parallèle
à BF et en E mener la tangente. Elle coupe BF
en A, et BD en C. ABC est le triangle demandé.

Discussion. - La construction est toujours possible si B est aigu.

215. - Construire un triangle rectangle, connaissant l’hypoténuse a et la somme
l des côtés de l’angle droit.
S.

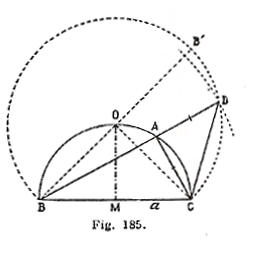
Supposons le problème résolu et soit
ABC (fig. 185) le triangle rectangle
demandé dans lequel : \(\widehat{BAC} = 90\)° ;
BC = a et : AB + AC = l .
Prolongeons le plus grand côté BA
d’une longueur AD = AC de telle sorte
que : BD = BA + AC = l ; puis menons
DC.
Le côté BC = a étant connu, le problème
serait résolu si l’on pouvait déterminer le
point D.
Or :

1. BD = l. Un premier lieu de D est
   donc la circonférence de centre B et de
   rayon l.
2. Dans le triangle CAD, l’angle CAD, supplément de l’angle droit BAC,
   lui-même droit.
   Or, par construction, AD = AC. Donc \(\hat{D} = \widehat{ACD}- 45\)°

BD = 1 ; \(\widehat {CDB} = B \) ; \(\widehat {CDB} = 135\)°.
Du point D, l’on voit BC sous un angle de 45° et un second lieu de D est, d’un côté
de BC, l’arc d’un segment capable de 45° décrit sur BC comme corde.
Le point D est à l’intersection des deux lieux.
On achève la construction en menant BD puis CA perpendiculaire à BD.

Discussion. - Désignons par 0 le centre du segment capable de 45° décrit sur BC comme corde ; c’est le milieu de la demi- circonférence de diamètre BC.
Pour que le problème soit possible, il faut que la circonférence de centre B et de
rayon 1 coupe l’arc CDB de la circonférence (O,OB), ce qui exige :
\(a < 1\leq 2 OB\).

218. - Construire un triangle rectangle connaissant un angle aigu B et la
différence [ des côtés de l’angle droit.

S.

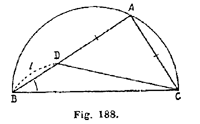
Supposons le problème résolu et soit
ABC (fig. 188) le triangle demandé dans
lequel : \( \widehat{BAC}= 90\)°, \( \widehat{CBA}= \hat{B}\) , AB-AC=l

Sur AB portons AD =AC, de telle sorte que l’on a
BD = AB-AC=l
Le triangle rectangle ADC étant isocèle, on a \( \widehat{ADC}= 45°\)
et par suite
\( \widehat{BDC}= 180-45= 135\)°
On sait alors construire le triangle BDC dont on connaît
BD = l ; \(\hat{D} = 45\)° ; \(\widehat{DBC} = 180 - \hat{B}\)
On achève en menant CA perpendiculaire à BD.

Remarque. - Nous avons supposé que B est
le plus petit angle aigu (\(\hat{B}<45)\)°)
et, par
suite, que AC < AB.

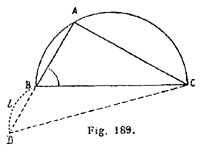
Si \(\hat{B} > 45\)° (fig. 189), on a : AC > AB ; le point D tombe au delà de B et l’on peut
construire le triangle BDC dont ou connaît :
BD =l ; \(\hat{D}=45\)° et \(\widehat{DBC}= 180-\hat{B}\)

On achève comme précédemment.
Le problème est toujours possible si B < 90°.

Un élément important de ce travail doit être souligné : à l’issue de chaque solution
intervient une « discussion » où les conditions de réalisation des figures ou de
validité des résultats sont détaillées. Nous pouvons l’observer pour les exercices cités
précédemment et pour l’exercice 211.

On achève la construction en menant BD puis CA perpendiculaire à BD.

211. _ Construire un triangle rectangle, connaissant la médiane nt et la hauteur
h relatives à l’hypoténuse.
S. Construction. - Construire le triangle
rectangle AHM (fig. 182)

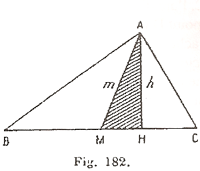
dont on connaît
l’hypoténuse AM = m et le côté AH = h.
On sait que la médiane relative à
l ’hypoténuse est égale à la moitié de
l’hypoténuse. Il suffit donc de porter sur MH
de part et d’autre de M les longueurs : MB =
MC=m.
ABC est le triangle demandé.

Discussion. - Il faut : \(h\leq m.\)

Un professeur enseignant à notre époque et désireux de faire utiliser par ses
élèves ce mode de raisonnement (<< Je suppose le problème résolu ») peut organiser
une séance de la façon suivante :

• Première étape : donner l’énoncé aux élèves et leur demander de réaliser la figure
  accompagnée de leur explication de cette réalisation.
• Deuxième étape : fournir le corrigé de Monsieur Béché aux élèves, comparer
  avec les méthodes qu’ils ont eux-mêmes proposées.
• Troisième étape : insister sur la « discussion » de la fin du corrigé fourni ; que se
  passerait-il si les conditions d’existence ou de validité n’étaient pas remplies ?

Du calcul de l’apothème du dodécagone régulier étoilé à l’étude détaillée des
coniques en passant par la géométrie descriptive et l’arpentage, l’ouvrage de M.
Béché a permis à de nombreuses générations d’élèves d’acquérir un bagage solide en
géométrie en y consacrant un temps plus limité que les élèves de lycées.

Un exemple d’énoncé permet d’illustrer ce propos et de montrer ce qu’on était en
droit d’attendre d’un élève de deuxième année :

« Sur les côtés d’un hexagone régulier de côté c et extérieurement à ce
polygone, on construit des carrés, puis on joint les sommets voisins de ces carrés.
Démontrer que l’on forme ainsi un dodécagone régulier convexe. »

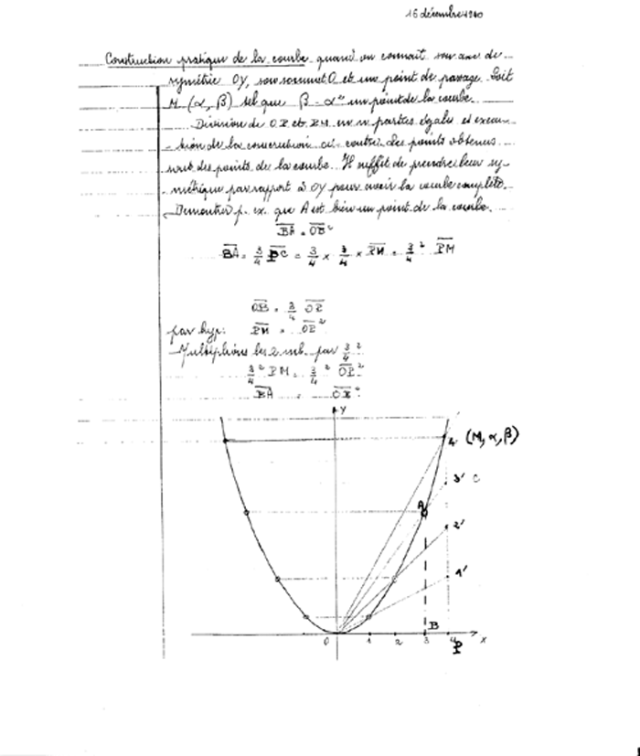
Construction pratique de la parabole

La lecture de cahiers d’écoliers peut être également riche d’enseignement.
Le document que nous publions ci-dessous a été écrit par un élève préparant le
concours d’entrée à l’école d’ingénieurs en 1940.
Il s’agit d’une question où interviennent analyse et géométrie : « Comment
construire une parabole dont on connaît le sommet, l’axe de symétrie et un point ? »
La démonstration est présentée pour le cas où OP et PM ont été divisés en quatre
parties égales, mais cette méthode reste valable pour d’autres partages de OP et PM
et son utilisation avec des élèves de seconde de lycée général ou professionnel est
tout à fait possible.

L’académie ... et les filles

Nous ne pouvons pas terminer notre propos sans évoquer deux points .

Le premier point concerne l’ Académie François
Bourdon, XIXe siècle (François
Bourdon ingénieur et inventeur du marteau-pilon).
Sa vocation est d’être un centre de
documentation et d’étude du patrimoine historique et industriel du Bassin du Creusot.
Elle dispose des archives de l’usine Schneider du Creusot et d’une bibliothèque
scientifique et technique de plus de huit mille volumes (depuis le seizième siècle
jusqu’à nos jours).
Elle se situe à côté du Château de la Verrerie au Creusot, les responsables et le
personnel sont très accueillants et les chercheurs bienvenus.

Le second veut apporter un complément par rapport au début de notre exposé : il
n’a pas encore été question des jeunes filles.
Or dès 1906, on a créé une école ménagère au Creusot ; son but est de développer
chez les filles des notions d’ordre, d’économie, d’adresse, de savoir-faire, les
préparant à devenir des jeunes femmes capables de rendre un jour leur intérieur
attrayant et de tirer le meilleur parti possible de leurs ressources.
«  Une bonne formation professionnelle des jeunes gens, en même temps
qu’elle rend d’importants services à l’industrie, contribue, dans une large
mesure, à l’amélioration du sort des familles qu’ils sont appelés à fonder.
Mais si l’on veut que ces familles atteignent leur plein développement, et
qu’elles remplissent vraiment leur rôle de " cellule sociale ", il ne suffit pas que
l’homme, accomplissant sa tâche avec habileté et conscience, apporte au foyer un
salaire rémunérateur, il faut que la femme, elle aussi, soit à la hauteur de son
devoir professionnel journalier, et ce devoir ne se résume-t-il pas, très souvent, à
être, suivant une vieille expression, une " bonne ménagère " ?  »
Les Établissements Schneider-Économie sociale. Nevers, 1912.

Dans l’école ménagère, les programmes comprennent un enseignement
théorique : économie domestique, comptabilité, hygiène, horticulture, et un
enseignement pratique : cuisine, nettoyage, raccommodage, confection du linge et
des vêtements, lavage ...
« Tout cela pour éviter le jour où le travailleur manuel, lassé de voir que son
intérieur ne lui donne point ce qu’il attendait, prend, pour ne plus le quitter, le
chemin du cabaret. »

Les Établissements Schneider-Économie sociale. Nevers, 1912.

Pour les jeunes filles de l’école ménagère, les mathématiques ne constituent pas
une matière enseignée, mais on leur fait suivre des cours de comptabilité ménagère
qui «  condense toutes les notions permettant à une femme d’obtenir le meilleur
rendement de ses ressources, d’établir le budget de son ménage, de tenir toujours en
ordre la comptabilité domestique, d’arriver progressivement à une meilleure
détermination de la part à faire à chacun des besoins ».