Claire Piolti-Lamorthe [1] & Sophie Roubin [2]

Résumé : Depuis quelques années, au niveau de l’école primaire et du collège, il apparaît, dans les discours institutionnels, une incitation à faire des activités rituelles et notamment ce qu’on désigne par calcul mental ou calcul réfléchi. Dans cet article, nous souhaitons initier une réflexion sur ce point et proposer des idées aux professeurs de collège pour mettre en oeuvre des activités rituelles de calcul réfléchi intégrées aux progressions et au travail fait dans les autres chapitres, notamment ceux de calcul littéral ou équations (inéquations). De plus, nous voulons présenter comment ces activités dites rituelles peuvent être intégrées dans les progressions de chaque classe et permettre d’anticiper sur les notions enseignées.

Depuis quelques années, il apparaît dans les discours institutionnels, une incitation à faire des activités rituelles.

Dans le Vade-mecum des principaux éléments de mathématiques (document ressource pour le socle commun), on trouve page 18 :
« Une préconisation forte consiste à proposer, lors de toute séance, un temps consacré à des activités rapides. Une telle pratique permet de traiter certaines notions dans la durée (sans y consacrer au total plus de temps) ce qui facilite aussi une mobilisation fréquente de ces notions. »

Dans cet article, nous souhaitons entamer une réflexion sur la ritualisation et proposer des idées aux professeurs de collège pour mettre en oeuvre des activités rituelles de calcul réfléchi intégrées aux progressions et au travail fait dans les autres chapitres, notamment ceux de calcul littéral ou équations (inéquations).

Enseignantes en collège, nous sommes associées depuis quelques années à un groupe de recherche INRP, SESAMES Algèbre. Nous cherchons à améliorer l’enseignement de l’algèbre au collège en favorisant les activités des élèves.

Nous avons été amenés à chercher comment développer le travail sur les techniques, travail important pour l’automatisation des calculs, sans que celui-ci ne devienne l’activité essentielle des séances d’algèbre, et nous avons ainsi travaillé sur l’articulation entre techniques de calcul et automatisation, mais aussi entre techniques de calcul et raisonnement. Ces deux points nous semblent particulièrement importants puisque nous faisons l’hypothèse que certaines techniques de calcul doivent être apprises et maîtrisées pour créer des automatismes qui serviront d ans la résolution de problèmes, mais aussi que le travail sur les techniques peut donner lieu à des justifications et des argumentations. Nous pensons donc que c’est là un vrai travail mathématique.

Dans un premier temps, nous allons définir ce que nous entendons par « calcul réfléchi » et en exposer différentes mises en oeuvre que nous pratiquons. Ensuite, pour aller plus loin, nous présenterons d’autres enjeux du calcul réfléchi.

1. Définition et mises en oeuvre du calcul réfléchi

Nous appelons calcul réfléchi, un calcul mental ou écrit qui nécessite de mettre en oeuvre une stratégie. Ainsi nous considérons que ce n’est pas parce que l’on fait des calculs que l’on se situe seulement dans une activité automatique comme peut l’être la mobilisation des tables de multiplication ou de procédures algorithmiques qui consistent à poser une opération. Il y a donc du raisonnement dans cette activité de calcul réfléchi. C’est d’ailleurs ce que souligne bien le texte du document d’accompagnement des programmes consacré au calcul numérique.
« Le calcul mental réfléchi nécessite l’élaboration de stratégies de calcul personnelles. Il met donc en jeu l’initiative, le raisonnement et des connaissances (explicites ou non) sur la numération et les propriétés des opérations. »

Nous avons choisi de débuter nos heures de cours par un court moment de recherche et par la correction d’un exercice que nous nommons « exercice rituel ». Au départ, ce temps était consacré à du calcul mental (instauration de règles, entraînement). Nous avons alors remarqué que les élèves étaient très concentrés durant ce petit temps de recherche, qu’ils se mettaient au travail dès le début, nous laissant le temps de faire l’appel et les vérifications de devoirs et de matériel. De plus, cela nous permettait de partager la séance en plusieurs moments : exercice rituel, correction du travail à la maison, poursuite du travail actuel (activité, leçons ou exercices). Nous avons donc utilisé ce temps d’« exercice rituel » pour entretenir tout au long de l’année les acquis, sans pour cela prendre une heure complète, et pour revenir de manière déconnectée sur certaines notions en amont d’un chapitre afin de préparer son introduction. De ce fait le thème des activités rituelles en début de chaque séance n’est pas forcément lié au chapitre en cours. La ritualisation nous offre la possibilité de travailler de cette manière sans que les élèves soient perturbés. En règle générale, le temps de recherche est de 5 minutes et le temps de correction 5 minutes. Cela a impliqué l’élaboration d’une progression intégrant les activités rituelles.

Dans le cadre des « exercices rituels », à chaque niveau du collège, nous pratiquons le calcul réfléchi. Les exercices sont corrigés immédiatement pour permettre aux élèves d’expliquer leur démarche. Notre objectif est de les rendre tous actifs en montrant la multiplicité des procédures et en cassant l’idée d’une procédure experte. Toutes les réponses sont prises en compte, explicitées, validées ou invalidées par la classe, puis en dernier ressort par l’enseignant.

Ce fonctionnement est inspiré de celui décrit dans la brochure « Calcul Mental » de l’IREM de Lyon, 2008 :
« En permettant à des élèves de réussir un calcul par des procédures personnelles avant de s’approprier une procédure automatisée, le calcul réfléchi est un moyen de gérer l’hétérogénéité. Au lieu d’enseigner des “ recettes ”, le professeur peut s’appuyer sur la diversité des procédures dans la classe pour permettre à chacun d’enrichir les siennes. »

Un des autres intérêts du calcul réfléchi est de favoriser les changements de cadres : langage naturel, schématisation, expression numérique, algébrique, … permettant une approche différenciée des notions. Cela permet aussi de s’affranchir des difficultés de la syntaxe et des notations de calculs pour réfléchir aux priorités opératoires, aux règles de calcul mental…
Voici quelques exemples d’exercices que nous proposons en lien avec les différents cadres.

Les différents cadres	Exemple d’exercice
Langage naturel.	Je choisis un nombre, je lui ajoute 4, je trouve 24. Quel nombre ai-je choisi ? La somme de 4 et d’un nombre est 24. Quel est ce nombre ?
Schématisation : Le recours aux programmes de calculs permet de présenter à l’aide d’opérateurs dans des flèches et met en évidence l’opération réciproque.
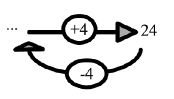
Expression numérique.	\(24-4=\) ou ?+4=24.
Expression algébrique.	Trouver x tel que x + 4 = 24.
Langage calculatrice. comme présenté dans le document ressource pour le socle commun dans l’enseignement des mathématiques au collège.	Zoé « a tapé » un nombre sur sa calculatrice, puis elle a appuyé sur les touches suivantes : Elle trouve 17. Quel nombre avait elle choisi ?

Après avoir donné ces quelques exemples, nous allons maintenant développer trois aspects du travail sur des calculs réfléchis qui dépassent largement ce cadre. Ces aspects sont :

• un point d’appui pour la maîtrise du calcul numérique et littéral,
• un point de départ pour les activités de preuve,
• une aide à l’acquisition d’automatismes pour les résolutions d’équations.
  

  2. Le calcul réfléchi : un appui pour la maîtrise du calcul numérique et littéral

  Au delà de la maîtrise du calcul numérique, une autre fonction du calcul réfléchi nous semble être de préparer le calcul littéral. C’est ce qui a été souligné aux Journées inter-académiques « Les nouveaux programmes de Mathématiques au Collège », 2 et 3 décembre 2004, La Grande Motte :
  Dans son aspect « réfléchi » le calcul mental nécessite, au contraire, une connaissance des nombres (qui s’affine avec l’entraînement) ainsi qu’une part d’initiative et de choix. Il opère sur des nombres et permet d’enraciner l’ordre de grandeur, le sens des opérations et leurs propriétés (commutativité, associativité, distributivité). C’est ainsi, qu’au Collège, il va devenir un moyen de préparation des compétences algébriques.

  Voici une idée de progression d’activités de calcul rituel qui se situe en amont des chapitres classiques d’algèbre.

  Dans un premier temps, les calculs proposés visent à automatiser des méthodes de calcul mental : compléments à l’unité, à la dizaine, à la centaine, maîtrise des tables de multiplication, divisions, calcul sur les fractions.

Combien y-a-t-il de 4 pour aller à 10 ? Opération à trous 5 + … = 40 Dans 16 combien y a t il de fois 4 ? 7 × … = 63 Écrire 72 comme un produit de deux nombres, trois nombres, … Calculer 5/7 de 28

Pour expliciter certaines règles de calcul mental, il peut être utile d’avoir recours à la schématisation. Par exemple, pour les additions :

528 + 1 314 = 1 310 + 520 + 8 + 4 = 1 830 + 12 = 1842 en montrant les groupes.

Ou bien pour les multiplications :

15 × 99 = … Réponse spontanée 15 × 100 − 15 (justifiée en Cinquième à l’aide de la distributivité : 15 × (100 − 1)).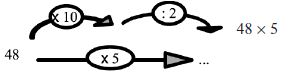 32 × 25 = 8 × 4 × 25 = 8 × 100 = 800. 32 × 25 = 32 × 100 / 4 = 3200 / 4 = 800. 32 × 25 = 32 × 50 / 2 = 1600 / 2 = 800. 156 est divisible par 13 car 156 = 130 + 26 = 13 × 10 + 13 × 2 = 13 × 12.

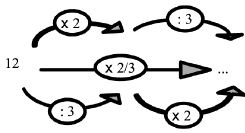
On utilise aussi cette schématisation pour travailler avec les élèves la multiplication d’une fraction par un nombre.

_ Calculer les \({2 \over 3}\) de 12.

La multiplication et la division se présentent comme deux opérations successives et commutatives sans l’obstacle de la syntaxe ou sans les présenter comme deux opérations séparées ; le but étant une prise de conscience par l’élève des différentes stratégies, plus ou moins efficaces, qui s’offrent à lui. Dans un second temps, à travers d’autres exercices, l’élève pourra choisir la méthode qui semble mieux lui convenir ou comprendra qu’il peut adapter son choix à la situation.

Le calcul réfléchi peut aussi nous amener à appliquer successivement deux opérations et à réfléchir aux priorités opératoires sans écrire ces opérations en ligne.

Je choisis un nombre. Je le multiplie par 3. J’ajoute 5 au résultat.

Je choisis un nombre. Je lui ajoute 5. Je multiplie le résultat par 3.

On demande alors aux élèves si les deux programmes vont donner le même résultat, puis on fait fonctionner le programme pour plusieurs nombres. On peut introduire l’écriture en ligne des calculs en faisant ressentir la nécessité de règles de priorités et l’utilisation des parenthèses. On peut même introduire une formule.

Pour le niveau Quatrième, nous ajoutons des calculs sur les relatifs et comprenant des carrés (ou des puissances autres, suivant le moment de l’année). Le calcul réfléchi permet dans ce cas un entraînement au calcul sur les relatifs.

Dès la classe de Cinquième, ces calculs enchaînés (et réitérés) seront généralisés en ayant recours aux lettres. Dans ce cas, le recours aux flèches permet de bien visualiser les éléments du calcul qui restent fixes et ceux qui varient (calcul procédural). Nous utiliserons donc le biais du calcul réfléchi pour entrer dans le calcul littéral.

Voici des exercices dans lesquels les simplifications d’écriture s’imposent et qui utilisent la factorisation :

3h + 25 min + 6 s + 5h + 12 min = (3 + 5) h + (25 + 12) min + 6s = 8h + 37 min + 6s. 3/4 + 7/4 = 3 × 1/4 + 7 × 1/4 = 10/4. À quoi est égal −3x + 15x pour tout nombre x ? À quoi est égal 4x − 7x pour tout nombre x ? Écris de façon plus simple : 12x − 8x, … Complète pour que les expressions soient égales pour tout nombre x : 5x + … = 2x. Complète pour que les expressions soient égales pour tout nombre x : 45x = 12x + … Je choisis un nombre, je lui ajoute 4, je multiplie le résultat par 3, puis je retranche deux fois le nombre de départ. Quel est le nombre choisi si je trouve 8 ? \(3\sqrt5-7\sqrt5=(3-7)\sqrt5.\)

On remarquera que nous insistons sur la quantification (pour tout …), car il nous semble important de préciser le statut des égalités dans le calcul littéral. Ceci n’est pas toujours fait (notamment dans les manuels). Nous pensons que cela ne permet pas aux élèves de faire la distinction entre une propriété générale et des égalités vraies pour une ou deux valeurs. Ainsi on dit toujours aux élèves que 3x + 7 = 10x est faux (en sous-entendant, que ce n’est pas vrai pour tout nombre x), mais on leur demande parfois de résoudre l’équation 3x + 7 = 10x (en sous-entendant, cette fois-ci, « existet- il un (ou des) nombre(s) tels que … »).

À travers ces petits exercices, nous visons l’acquisition d’automatismes de calcul (numériques ou littéraux) qui serviront dans des calculs plus complexes. Nous pensons également que cela favorise une meilleure compréhension des opérations sur les nombres fractionnaires ou relatifs. Nous introduisons des outils transitoires tels que les schémas et enfin nous souhaitons favoriser l’évolution des procédures plus ou moins expertes par la confrontation entre les élèves.

3. Le calcul réfléchi : Un point de départ pour les activités de preuve

Dans cette partie, nous commençons à introduire des types de problèmes classiques sur les preuves en algèbre. Nous proposons tout d’abord des programmes de calcul dont le résultat (remarquable) peut être prouvé grâce à une réduction.

Je choisis le nombre 3, je lui ajoute 4, je multiplie le résultat par 5, puis je retranche 20. Calculer le résultat obtenu. Faire de même avec 6, 8, 48. Que remarquez vous ?

Le programme renvoie 5 fois le nombre choisi au départ ; les élèves peuvent remarquer ce résultat particulier (éventuellement dès la Sixième en justifiant par le fait que l’on ajoute 4 × 5, puis que l’on soustrait 20) et le prouver grâce à la distributivité.

Pour les niveaux Quatrième et Troisième, la preuve pourra faire appel à la double distributivité ou aux identités remarquables pour factoriser.

Nous proposons ensuite aux élèves de créer leurs propres programmes, que leurs camarades devront découvrir en le faisant fonctionner plusieurs fois. Ils seront donc amenés à mettre en oeuvre des stratégies de recherche. Les nombres ne sont plus choisis au hasard : importance du 0, recherche d’une proportionnalité ou d’une proportionnalité décalée (fonction affine), …

L’élève responsable fabrique son programme de calcul. Par exemple 3 donne 7. Ensuite ses camarades proposent des nombres avec lesquels le faire fonctionner : par exemple, 2, espérant trouver 2 × 2 + 1 = 5, 9, espérant trouver \(9\times {7 \over 3}=21\) 1, espérant trouver 1 + 4 = 5.

En fin de Quatrième et en Troisième, on constate que certains élèves vont s’appuyer sur une représentation graphique pour raisonner.
_

4. Le calcul réfléchi : une aide à l’acquisition d’automatismes pour les résolutions d’équations

Dès la sixième, la recherche de complément ou les opérations à trous peuvent fournir une première approche des équations, le travail portant cette fois sur l’idée de chercher l’opération réciproque. L’utilisation des flèches prend ici tout son sens.

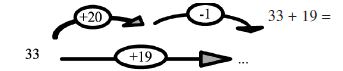
Je choisis un nombre. Je le multiplie par 3. J’ajoute 5 au résultat. Quel nombre ai-je choisi si j’obtiens 17 ? 6 ?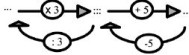

Je choisis un nombre. Je lui ajoute 5. Je multiplie le résultat par 3. Quel nombre ai-je choisi si j’obtiens 24 ?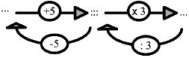

On montre alors aux élèves que pour démonter le calcul on utilise l’opération « inverse » de chaque opération du programme en commençant par la dernière.

Pour préparer les élèves à l’abstraction, nous proposons régulièrement, et dès la Sixième, des écritures littérales dont on demandera aux élèves de les « démonter » dans le but de les faire réfléchir aux opérations et aux priorités correspondant à une écriture.

Quelles transformations fait-on subir à k pour avoir … k/6 + 2 ? Comment retrouver z si je connais 5 × (z + 2) ?

Cela permettra d’avoir recours au vocabulaire somme, produit, ...

56 est la somme de 12 et du produit de 2 par … ? 68 est la différence entre … ? et 17.

Nous donnons ensuite le programme sous la forme d’une phrase, en Cinquième seulement, avec l’opération réciproque.

Quel est le nombre qui, ajouté à 8, donne 24 ? Je pense à un nombre, je lui enlève 12 et j’obtiens 34. Quel est ce nombre ? Je cherche le nombre qui, lorsque je lui ajoute 4 et que je multiplie le résultat par 9, donne 63.

En Quatrième, nous proposons des programmes de calculs agissant sur l’inconnue dans les deux membres. Nous avons ainsi un enchaînement de plusieurs exercices dans lesquels nous modifions les variables didactiques pour permettre aux élèves de trouver, dans un premier temps, la solution par tâtonnement (solution entière, simple), puis de les amener intuitivement vers les règles d’opérations sur les égalités. On continue avec des problèmes ayant les mêmes solutions pour permettre aux élèves de comprendre ces règles. Durant ce travail, qui est très en amont du chapitre sur les équations, aucune formalisation n’est exigée. Voici un exemple d’une telle progression.

Trouver x tel que si je le multiplie par 5 et que j’ajoute 2, je trouve le même résultat que si je le multiplie par 3 et que j’ajoute 6 (solution entière, trouvée souvent par tâtonnement). Trouver x tel que si je le multiplie par 6 et que j’ajoute 5, je trouve le même résultat que si je le multiplie par 3 et que j’ajoute 7 (solution fractionnaire qui nécessite d’avoir mis au point certaines stratégies). Trouver x tel que si je le multiplie par 5 et que j’ajoute 5, je trouve le même résultat que si je le multiplie par 2 et que j’ajoute 7 (solution identique à la précédente, les élèves peuvent remarquer une relation entre les équations). Nina et Nino choisissent un nombre, Nina lui ajoute 3 et multiplie le résultat par 5 et Nino le multiplie par 6 et retranche 10. Ils trouvent le même résultat. Quel est ce nombre ? Ou avec la procédure calculette : Nina et Nino ont chacun une calculatrice. Ils ont « tapé » le même nombre. Ensuite, Nina a appuyé sur les touches : et, Nino a appuyé sur les touches : Surprise ! Ils obtiennent aussi le même résultat ! Quel nombre ont-ils bien pu choisir ?

La complexité augmentera en Troisième en travaillant sur les inéquations et les équations produit.

Conclusion

Dans cet article, nous avons proposé des activités que nous utilisons avec nos élèves pour renforcer en particulier leurs compétences techniques, par le biais de « l’exercice rituel » que l’on fait en début de chaque séance. Ce temps est, pour nous, un point d’appui pour la maîtrise du calcul numérique et littéral, un point de départ pour les activités de preuve et enfin une aide à l’acquisition d’automatismes pour les résolutions d’équations.

Nous pensons avoir également montré comment, par une progression adaptée, on peut commencer à travailler sur des notions algébriques avant de traiter les chapitres classiques qui auront alors pour but de faire le point, d’institutionnaliser les savoirs qui ont été vus et de traiter des problèmes plus complexes.

Il nous semble maintenant que ce travail nous amène à nous interroger sur la structure des séquences de classe et sur le découpage classique en chapitres correspondant soit à des titres de paragraphes du programme, soit à ceux des chapitres des manuels.

Nous pensons que l’on peut envisager de changer ce découpage, en effectuant les révisions des thèmes classiques en amont des chapitres, en se limitant aux notions nouvelles durant la partie classique du cours et en prolongeant le travail sur les automatismes en aval. Ainsi dans ce nouveau découpage, plusieurs chapitres seront amenés à fonctionner en parallèle.

Ce sont des idées que nous souhaitons approfondir dans la suite de notre travail(1).

(1) L’origine de ce travail provient d’un groupe de recherche innovation soutenu par l’INRP, dans le cadre de l’UMR ICAR, groupe COAST, appelé SESAMES (Situations d’enseignement scientifique, activités de modélisation, d’évaluation et de simulation).
Vous pouvez vous faire une idée de notre ligne directrice en visitant notre site :
http://web.lyon.iufm.fr/UCDmath/algebre/index.htm
Les membres de Sésames Algèbre : La responsable : Sylvie Coppé, les professeurs associés : Christophe Alves, Vincent Duval, Sté phane Garapon, Sylvie Martin-Dametto, Claire Piolti-Lamorthe, Sophie Roubin.

Un jugement sur Euclide « Je citerai celui qui, à mon humble avis, est le roi des cons. J’ai nommé le célèbre mathématicien Euclide qui affirme sans rire, je cite : “ La ligne droite est le plus court chemin d’un point à un autre.” Quelle connerie ! Chacun sait en effet que la ligne droite ne peut être le plus court chemin d’un point à un autre. Sauf, évidemment, si les deux points sont bien en face l’un de l’autre. » Pierre Desproges, Manuel de savoir vivre, coll. Points, p 97.

<redacteur|auteur=500>