Ayant relu récemment les brochures « jeux » de l’APMEP, et plus particulièrement
la première d’entre elles, qui est loin d’être désuète, j’ai été tenté de faire jouer des
élèves d’une classe de CM2 au « quinze-vainc ». La brochure précise que ce jeu a
été expérimenté en classe de seconde. Comment pouvaient réagir des élèves de CM2
avec ce même jeu ?

J’ai proposé à Christiane Longeron, Maître Formateur à l’École Jean-Jacques
Rousseau à Colmar de jouer au jeu dont voici la règle . Elle
joue et me dit aussitôt : « je vais le faire dans ma classe » et elle m’invite à
participer à ce travail avec ses élèves de CM2.

Travail ? D’aucuns pourraient penser que jouer en classe est une perte de temps, que
les enseignants ont des programmes à respecter, que les activités à proposer aux
élèves doivent en découler directement et que, les instructions officielles ne
préconisant pas un enseignement par le jeu, celui-ci ne devrait pas réellement trouver
sa place en classe, sauf à conduire à des apprentissages immédiats, clairement
identifiés a priori. Nous avons fait le pari que ce jeu permettrait aux élèves à la fois
de mettre en œuvre des savoirs mathématiques établis et peut-être même de découvrir
des objets mathématiques ou des outils nouveaux.

Nous avons donc introduit ce jeu
dans une classe de CM2 et ce court texte est un témoignage de cette activité.

Jeu ? Je ne voudrais pas, dans ce court
témoignage, préciser ce que peut être jouer, mais
je rappellerai cependant ce qu’en dit Gilles
Brougère [1]. Pour lui, jouer est une activité qui
vérifie cinq critères. Il s’agit d’une activité
frivole, de second degré en ce sens qu’elle se
situe dans un tout autre plan que celui de la vie
réelle, qui obéit à une règle, dans laquelle on
prend des décisions et qui reste marquée par
l’incertitude.

On appelle souvent « jeux éducatifs » des
activités qui ne respectent pas tous ces critères,
mais qui sont pratiquées en classes sous
l’appellation de « jeux ». Le mathématicien
désigne souvent par le mot « jeu » des activités
que d’autres appelleraient « énigmes » et qui
sont en fait des problèmes.

Laissons jouer les élèves.

Première phase : nombres invisibles

Cette première phase qui s’est déroulée pendant une première séance d’une durée
d’environ une demi-heure est destinée à familiariser les élèves avec la règle du jeu :
notamment avec l’alternance des prises de cartes et le fait que c’est le premier joueur
qui a trois cartes dont la somme des nombres indiqués est égale à quinze qui gagne.

Elle est aussi destinée à montrer la différence qu’il peut y avoir entre un jeu au hasard
et un jeu où l’élève peut développer une stratégie.

La première phase du jeu consiste donc à faire jouer les élèves, sans autre contrainte
que le hasard. La règle est rappelée dans le cadre ci-dessus, mais les nombres inscrits
sur les cartes [2] ne sont pas visibles (jeu à cartes retournées).

Chaque groupe de deux joueurs joue dix parties et note le nombre de parties gagnées
par l’un et par l’autre.

Les élèves se prennent au jeu, mais gagnent peu...

Les résultats sont alors mis en commun et consignés dans un tableau sur une grande
feuille de papier. La classe comporte dix groupes, il y a donc cent résultats.

La maîtresse demande aux élèves comment on fait pour gagner...
Les réponses sont
évidentes ... on ne fait rien. C’est le hasard qui fait gagner ou perdre. Personne n’est
maître de son jeu. Les seules décisions à prendre concernent le choix de telle ou telle
carte, mais en aveugle...

Les élèves estiment que ce jeu n’est pas bien intéressant.

Note : Toute la suite s’est déroulée pendant une seule séance d’une durée d’environ
une heure trente.

Deuxième phase : nombres visibles

Le but de cette phase est de permettre aux élèves de se rendre compte qu’en
réfléchissant, ils peuvent modifier considérablement les résultats du jeu.

Les cartes
sont donc disposées sur la table, nombres visibles.

Les élèves jouent, mais cette fois bien
moins vite que dans la phase précédente.
Chaque groupe d’élève note les parties
gagnées, et qui les a gagnées.

Le
nombre total de parties jouées n’est
plus que de quarante (dans le temps
réservé à cette phase de jeu, environ
dix minutes).

Un tableau récapitulatif
est rempli.

Il convient de le commenter
et de l’interpréter.

Mais auparavant, nous avons demandé aux élèves ce qu’ils pensaient de ce jeu et des
deux phases différentes.

Les réactions sont nombreuses :

«  c’est comme le morpion »... pourquoi ? demande la maîtresse, « parce qu’il faut
empêcher l’autre de gagner » répond l’élève.

Un autre élève précise : « c’est un jeu de stratégie ». On lui demande ce qu’est une
stratégie, il répond en prenant un exemple militaire.

Quelques remarques sont notées sur feuille et affichées.

Le fait que le nombre de parties faces des cartes cachées soit de 100 et que celui des
cartes vues ne soit que de 40 invite à une réflexion imprévue au moment de la
préparation de la séance de jeu.

On compte collectivement le nombre de parties gagnées dans la première phase et
celui de la deuxième phase.

Il y a 18 parties gagnées sur 100 parties jouées au hasard et 29 parties gagnées sur 40
jouées en connaissant les cartes sur la table ainsi que celles de l’adversaire
(partenaire). Si la différence est évidente, la maîtresse demande quand même de
préciser.

«  En supposant que l’on ait joué cent parties de la même manière que les quarante
premières, combien de parties gagnées aurait-on eues ? »

Un élève, souvent refermé sur lui-même, dit «  de quarante pour faire cent, il faut
prendre deux fois quarante et encore la moitié »... et détaille ce qu’il faut écrire au
numérateur pour obtenir un dénominateur égal à 100 sans changer la valeur du
rapport.

Ce raisonnement, qui met en œuvre implicitement un raisonnement par
proportionnalité, en mobilisant les propriétés de linéarité est explicité à la classe et
conduit aux écritures suivantes au tableau :

Les élèves sont invités à exprimer le résultat en pourcentages, comme si la deuxième
partie avait porté sur cent jeux.

Cette demi-partie entre la soixante-douzième et la
soixante-treizième n’est qu’un demi-problème... « c’est pas vraiment comme si on
en avait jouées cent ».

La conclusion s’impose : on gagne beaucoup plus en réfléchissant. Les élèves
trouvent bien plus intéressant le deuxième jeu car « on réfléchit ».
Un bon point
pour les mathématiques qui deviennent intéressantes car elles sont un lieu de
réflexion. Mais,au fait, réfléchit-on toujours en cours de mathématiques ?

Les élèves sont enthousiastes quand on leur demande s’ils souhaitent trouver
comment ne jamais perdre.

Vers l’émergence d’une stratégie

Nous demandons aux élèves de trouver tous les choix possibles de trois cartes dont
la somme des nombres marqués vaut 15.

Le travail se fait individuellement, mais les élèves coopèrent volontiers entre eux.
Les écrits ne sont généralement pas organisés.

Une phase collective très rapide suit
cette phase de recherche.

On écrit au
tableau, dans l’ordre indiqué par les
élèves, l’ensemble des solutions qu’ils
ont trouvées.

La classe, dans son
ensemble les a toutes trouvées, mais seulement
quelques groupes avaient trouvé
les huit solutions possibles.

Toutes les solutions figurent au tableau,
mais nous disons aux élèves qu’il
manque deux solutions.

La classe, dans
un silence impressionnant, se remet au
travail. Il ne s’agirait pas d’oublier des
configurations gagnantes. Au bout de
quelques minutes, la classe s’agite un
peu... « Monsieur, on n’en trouve pas
d’autre ! ». Cette remarque est reprise en
chœur par tous les élèves.

Nous leur faisons alors remarquer que s’ils s’étaient tous remis à travailler si
sérieusement c’est bien parce qu’ils n’étaient pas sûrs d’avoir écrit au tableau toutes
les solutions.

La question de savoir comment on peut être certain d’avoir toutes les
solutions leur est alors posée collectivement.

Après un court instant, une petite fille
déclare « on n’a qu’à commencer par
le plus grand »...

Elle explicite, on
écrit d’abord le plus grand nombre dans
la décomposition. Puis elle ajoute « 
ensuite on écrit le plus petit »... Interrogée
sur la logique de ses propos elle
finit par dire qu’on écrit ensuite le plus
grand des deux et que le plus petit sera
écrit en dernier.

Nous demandons donc aux élèves de
construire de cette manière le tableau de
toutes les solutions. Le travail semble
un peu difficile au début pour certains
groupes, mais tous finissent par y arriver.

Ils viennent de découvrir un outil de
démonstration par exhaustivité.

Les parties sont nulles.

Les élèves sont invités à jouer à nouveau en s’aidant du tableau ainsi construit. À part
deux groupes où un élève a gagné, toutes les parties sont nulles. Personne ne peut plus

perdre puisque chacun peut empêcher l’autre de gagner ! Catastrophe, c’est la
mort du jeu.

Les élèves qui ont gagné ont réussi une fois contre une faute de calcul,
l’autre contre une étourderie (explications des élèves).

Nous proposons aux élèves d’aller un peu plus loin et de construire un nouvel outil,
plus simple à utiliser et qui leur permettra aussi de ne jamais perdre.

L’enthousiasme
n’a pas baissé dans la classe.

Vers un carré magique

Nous dessinons au tableau noir un
tableau 3 × 3 et montrons aux élèves
qu’il y a trois lignes, trois colonnes et
deux diagonales.

En tout cela fait donc huit alignements.

Nous leur demandons de placer tous les
nombres de 1 à 9 dans ce tableau, de
manière à ce que la somme des nombres
marqués sur chaque ligne, chaque
colonne ou chaque diagonale soit égale
à 15.

Les tâtonnements ne sont pas très fructueux.

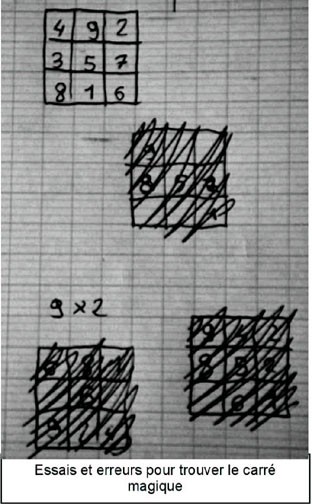
Pour ce faire, il va être bon de
réfléchir en observant le tableau réalisé
précédemment.

Nous leur suggérons
d’observer combien de fois chaque
nombre apparaît dans les décompositions.

Les élèves dressent dont le
tableau ci-dessous.

1		2		3		4		5		6		7		8		9
2		3		2		3		4		3		2		3		2

Il serait peut-être possible à ce moment là de parler d’effectifs.

Certains élèves
suggèrent de prendre le 5 quand on joue parce qu’il apparaît le plus souvent...

Ce
tableau va aider les élèves à organiser le tableau magique. Certains tâtonnent car ils
n’ont pas remarqué que les nombres qui apparaissent trois fois doivent se placer dans
les coins, d’autres qui ont fait cette remarque placent ces nombres de manière
aléatoire et sont contraints à reprendre plusieurs fois leur travail.

Une fois ce travail réalisé, il est aisé de revenir à la remarque d’une élève... « c’est
comme le morpion ».

Nous dessinons alors un tableau 3 × 3 pour y jouer au « morpion ».

Deux élèves
jouent et ont fait apparaître parallèlement les variations dans l’un et l’autre des deux
jeux.

Les élèves quitteront cette séance sûrs de ne jamais perdre à ce jeu qu’ils proposeront
à leur entourage.

Mais qu’ont-ils appris en mathématiques ?

Quelles mathématiques ont été mises en œuvre ?

Il nous semble que ce jeu, comme de nombreux autres jeux qu’il est possible
d’introduire en classe, permet aussi de faire des mathématiques, de les faire
autrement, encore est-il nécessaire de les pointer et que l’élève en conserve une trace
écrite.

Examinons brièvement les mathématiques mises en œuvre.

Du point de vue du calcul

Travail sur les décompositions additives, sur les compléments d’une somme à quinze.

Travail sur la proportionnalité : utilisation empirique des formules de linéarité pour

trouver un
rapport égal à un rapport donné (la proportionnalité n’est pas au programme, mais on peut
l’approcher, notamment en mettant en œuvre ces formules).

Comparaison de deux rapports.

Travail sur les pourcentages.

Approche de la notion d’effectifs, de fréquence, etc.

Du point de vue de la logique

Élaboration d’un outil de démonstration par exhaustivité (par rangement systématique).

Respect de contraintes (dans le jeu, dans l’organisation des nombres dans le carré

magique).

L’emploi d’expressions comme « si ... alors ».

Du point de vue de l’heuristique

Travailler par essais et erreurs en vue de l’élaboration du tableau magique en tenant

compte
des effectifs d’apparition des nombres dans les décompositions.

Outre les mathématiques, la pratique de ce jeu contribue vraisemblablement au
développement personnel de l’enfant qui doit :

 travailler dans le respect de règles,

 prendre le point de vue de l’autre, se mettre à sa place (pour anticiper ce qu’il

pourrait
faire),

 prendre des décisions et en assumer les conséquences (sans conséquences autres pour lui
que celles liées au jeu, celui-ci étant « futile ».

Traces écrites

Il paraît fondamental de conserver des traces écrites des mathématiques ou des outils
logiques découverts pendant le jeu et les phases de mise en commun.

Ces traces pourront être réalisées de manière personnelle, faisant par exemple état
des errements dans la recherche, des méthodes utilisées pour parvenir à une
découverte, à une solution ou à une stratégie pertinente.

Une partie collective,
rédigée en commun sous la direction du maître, concernera essentiellement les
mathématiques ou les aspects logiques (par exemple formaliser l’outil de
démonstration par exhaustivité).

Ces traces seront alors des références communes à l’ensemble de la classe et
serviront d’outils par la suite. Une partie d’entre elles pourra même faire l’objet d’un
affichage dans la salle.

Prolongements possibles

Les prolongements possibles en mathématiques peuvent se situer au niveau de la
consolidation des acquis ou consister en une ouverture vers d’autres découvertes.

Consolidation des acquis

L’organisation systématique des données, pour parvenir à garantir l’exhaustivité doit
être consolidée par diverses autres activités de nature analogue : décomposer
systématiquement d’autres nombres en sommes de deux, trois ou quatre autres
entiers, décomposer des nombres en produit de facteurs afin de les trouver tous, etc.

Nouvelles découvertes

La situation porte à définir des fréquences relatives, à travailler sur des rapports, des
pourcentages, pourquoi ne pas le faire ?

Les élèves peuvent aussi être invités à trouver comment, à partir d’un carré magique
on peut en fabriquer d’autres, comment donc construire d’autres jeux analogues avec
d’autres valeurs numériques. Ce qui oblige à entrer dans une démarche d’analyse,
activité essentielle à développer en classe.

Conclusion

Le jeu de stratégie en classe peut être formateur pour l’esprit par les facultés de
réflexion qu’il impose, par l’aspect ludique qui motive les élèves à combiner activités
mathématiques et logiques, par les mathématiques nouvelles qu’il permet
éventuellement de découvrir.

J’ajouterais volontiers que ses bénéfices pourraient
rapidement s’estomper s’il n’était accompagné d’écrits organisés individuellement
ou collectivement par le maître ou sous sa direction.