Guy Brousseau
IUFM d’Aquitaine et LADIST, Bordeaux1

 

« Qu’est-ce que "faire des mathématiques" à l’école primaire selon vous ? ». La question posée par l’APMEP m’a laissé rêveur. Je me suis senti le désir, et la crainte, de jouer les capitaine NEMO : « Voulez vous faire un voyage de vingt mille lieues sous les mathématiques ? » Car les mathématiques du primaire sont pour moi comme l’océan. Elles déterminent le niveau 0 mais elles sont profondes et riches, c’est d’elles que surgissent les hardis conquérants des continents mathématiques mais elles recueillent aussi parfois leurs déchets.

Et bien soit, essayons toujours ! Qu’est-ce que "faire des mathématiques à l’école primaire ?" pour la plupart des enfants, pour leurs parents et pour leurs maîtres ?

Nous connaissons tous l’école primaire de l’intérieur. Alors, lorsqu’on parle des connaissances qu’on y enseigne, nous croyons tous parler de la même chose, à des différences personnelles, subjectives et folkloriques près. Ce n’est pas si sûr. Pour bien comprendre la beauté et la difficulté de la tâche des uns et des autres, je propose d’observer ce qui les assujettit les uns aux autres : la transmission des connaissances.

Les mathématiques à l’école, c’est d’abord apprendre à compter.

Apprendre à compter

Scène familiale

Bébé compte

Maman : — Vous savez, grand père, le petit sait compter !
Grand père : — C’est vrai ? voyons ça mon mignon …
Maman : — "Montre à grand père que tu sais bien compter"
L’enfant, quatre ans : — Un, deux, trois, quatre, cinq, six, sept, huit, dix, quinze, heu …
Grand père, admiratif :— Aaah ! très bien ! Il ne te reste plus qu’à continuer !

Mais "compter" ne compte pas

Mais la tante Mimi, qui est une institutrice à la retraite, intervient :
Tante Mimi : — Mais non, grand père, pour savoir si cet enfant sait compter il faut lui montrer des doigts et lui demander combien il y en a, et puis lui demander à son tour de montrer tant de doigts ! il ne suffit pas de réciter la suite des nombres ! Et s’il n’y parvient pas bien, il ne faut pas que maman soit déçue. À quatre ans la plupart des enfants ne peuvent guère vraiment comprendre les nombres au delà de 5, les psychologues vous le diront.
Maman : — Mais notre petite voisine Odile, qui a cinq ans, compte bien jusqu’à soixante et dix !
Tante Mimi : — Oui, elle peut aussi réciter « Le chat la belette et le petit lapin » qui comporte bien plus de 70 mots, mais elle croit que les pénates sont des espèces de pantoufles ! Ce n’est pas bien grave, mais une jeune collègue m’a raconté que les parents exercent actuellement une forte pression pour "faire compter" précocement les enfants. Elle constate que sous l’influence de ce matraquage, certains de ses élèves se mettent à compter, dès lors qu’ils entendent le mot "nombre" sans même vouloir réfléchir à la question qu’on leur pose. Elle a dans sa classe des élèves "petits et moyens" d’école maternelle, des enfants qui comptent mécaniquement jusqu’au delà de cinquante, et de ce fait, elle ne peut plus, ni avec eux, ni avec ceux qui ne dépassent pas cinq, organiser en commun aucune activité mathématique de leur âge.

Projet scolaire

Dénombrer

Considérons la situation suivante qui peut être traduite en instructions adaptées aux enfants de 5 à 6 ans :
"Nous avons des peintures dans ces petits pots. Tu dois aller chercher là-bas les pinceaux et en mettre un seul dans chaque pot. Tu dois porter tous les pinceaux en un coup et il faut qu’il ne reste ni pinceau sans pot, ni pot sans pinceau. Si tu te trompes, tu reprends tous les pinceaux, tu les ramènes là-bas et tu essaies à nouveau. Tu sauras compter quand tu pourras faire ça, même quand il y a beaucoup de pots".

Plus précisément, l’enfant saura dénombrer lorsqu’il pourra jouer les deux rôles : demander (émetteur) à quelqu’un (récepteur), oralement ou par écrit, la quantité de pinceaux nécessaires en vérifiant l’opération, et inversement fournir à la demande la quantité voulue.

Une telle situation présente un caractère fondamental parce que "toutes" les situations de comptage peuvent être décrites en faisant varier ses variables cognitives et que toutes les pratiques de comptage et d’apprentissage du comptage peuvent ainsi être classées et comparées du point de vue didactique. Les pratiques habituelles du comptage, celles que nous avons présentées ci-dessus, s’obtiennent à partir de la situation fondamentale par suppression ou par transfert à l’adulte de certaines tâches. Dans la première, que nous pourrions appeler par exemple "le comptage populaire", l’enfant reproduit une suite de mots sous le contrôle de l’adulte. La seconde, "le comptage scolaire classique", est plus évoluée, il reste à l’enfant à faire correspondre un nombre à un ensemble de pots (travail d’émetteur), ou à constituer un ensemble d’un nombre donné de pinceaux.

Apprendre à compter

Apprendre séparément ces pratiques partielles implique que l’adulte les enseigne, les exige, les corrige, les fasse imiter et répéter. À aucun moment, l’enfant n’est en mesure d’établir lui-même la finalité de l’action et de corriger ses erreurs. Cependant, parents et enseignants utilisent avec un certains succès toutes ces formes dégénérées de la situation fondamentale, même le cas extrême de l’apprentissage formel de la suite des nombres. Aussi s’agit-il moins de rejeter certaines d’entre elles que de les utiliser au mieux suivant leurs caractéristiques particulières. Les désavantages principaux des apprentissages partiels sont les suivants :

• ils ne permettent pas de déférer à l’enfant la responsabilité du jugement sur la valeur de ses réponses, ni de lui décrire à l’avance un projet d’apprentissage dont il peut évaluer les progrès
• il faut qu’il ait déjà appris la réponse d’une manière ou d’une autre pour comprendre ce qu’on lui demande de faire.

La "définition" didactique est différente : elle replace les techniques dans une action globale intelligible. Elle n’exige pas que l’enfant sache déjà compter pour la comprendre. Il est seulement nécessaire qu’il puisse réussir le jeu avec deux ou trois pots. Il faut aussi qu’il sache vérifier la correspondance un à un. L’apprentissage alors peut commencer, non pas par l’imitation ou la reproduction mais. par l’invention de solutions stables quel qu’en soit le moyen.

Apprendre les nombres

Finalement, il faudra bien, pour cela, qu’il énumère [1] les collections (qu’il appelle l’un après l’autre, tous les objets sans appeler deux fois le même), en même temps qu’il les dénombre (qu’il évalue leur cardinal par correspondance avec une autre collection), en particulier quand il les compte (qu’il met en correspondance leurs éléments avec les mots) puis, si le comptage a été décomposé, en "nombrant" (en exprimant oralement le nombre à l’aide d’un système de numération) le résultat de son comptage, et ensuite en écrivant ce nombre. Il faudra aussi qu’il s’approprie les usages ordinaux de la suite des nombres etc.

Mais ces apprentissages pourront se produire par une conjonction de méthodes :

• par exemple dans un processus constructiviste, en complétant les réponses spontanées, ou provoquées avec les institutionnalisations indispensables,
• ou dans des enseignements plus classiques, maïeutique ou même axiomatique, avec des leçons suivies d’exercices, en réponse au problème désormais bien identifié par l’élève.

De même la situation fondamentale ne discrédite aucune des formes d’apprentissages. Elle les permet toutes et permet de les conjuguer : elle complète les apprentissages partiels qui restent utiles et sans doute nécessaires, et surtout elle leur donne leur sens.

L’usage purement numéral des nombres (pour seulement identifier ou désigner un objet : numéro de chaîne TV, de téléphone, ou d’automobile) ne semble présenter, lui, aucun problème. Sans doute parce que la difficulté principale réside moins dans l’apprentissage des automatismes que dans la connaissance des propriétés des collections, des nombres et de leurs opérations. Celles-ci doivent être obligatoirement "connues" de l’élève pour qu’il puisse contrôler leurs usages complexes.

Il faudra de plus, tôt ou tard, ne pas se contenter de leur usage, mais aussi élucider, formuler, discuter les propriétés et les structures numériques. Ces élucidations sont nécessaires à l’apprentissage lui-même et doivent l’accompagner. Comment et quand ?

Comprendre le dénombrement

Une expérience

Ce sens, dans les cas classiques, ne vient qu’après. Pour s’en convaincre, il faut interroger des enfants en cours d’apprentissage (classique), qui "savent" déjà compter en ce sens qu’ils savent résoudre le problème de l’émetteur et celui du récepteur (disons jusqu’à trente), mais qui n’ont pas encore la maîtrise du dénombrement. B. VILLEGAS a pu observer le comportement suivant :

L’élève va chercher une poignée de pinceaux et les distribue dans les
pots.
— "Ah, il en reste trois !"
— Tu as réussi ?
— Non parce qu’il m’en reste trois !
— Bon, reprends-les tous et essaie une autre fois.

Les autres élèves de la classe lui suggèrent : "compte !, compte !"

L’élève compte les pots, repart, saisit une poignée de pinceaux et revient. Le fait de compter ne lui a servi à rien. Les autres élèves continuent à l’aider :
— Non ! non ! tu dois compter les pinceaux.

L’enfant part, compte tous les pinceaux et revient …

Cet exemple met en évidence une différence entre le comptage comme savoir culturel habituel et le comptage comme connaissance d’un moyen de résoudre la situation fondamentale.

Une condition supplémentaire : la confiance en ses méthodes

Pouvons-nous affirmer que l’élève sait compter lorsqu’il est capable de constituer des collections adéquates de quelque importance dans les conditions ci-dessus ?

Pas tout à fait : Il doit aussi être capable d’être suffisamment sûr de son comptage pour identifier les sources d’erreurs et au besoin les discuter.

Par exemple, si au moment où il va chercher les pinceaux, quelqu’un lui dérobe un pot, il doit être capable de dire : — "tu m’as fait une farce !".

Cette confiance dans ses méthodes exige à son tour une position réflexive par rapport à elles, une "métaconnaissance", des mots pour exprimer les connaissances acquises, un métalangage, et finalement tout ce qui constitue la conversion en savoirs de certaines des connaissances.

Ainsi notre situation de dénombrement n’était pas tout à fait fondamentale. L’est-elle maintenant ?

Par rapport aux méthodes classiques, elle peut se révéler utile, à divers moments de l’apprentissage et surtout pour indiquer aux professeurs ce que veut dire "compter" en termes "concrets". Ceci ne veut pas dire que l’apprentissage par l’usage exclusif de la situation fondamentale serait plus rapide ou plus efficace, elle peut se révéler inutilement lourde quand l’élève a compris le but de l’apprentissage.

Premières réflexions

Sur la transposition

Notre premier exemple montre bien que tout le monde n’a pas le même rapport aux mêmes notions mathématiques et ne leur donne pas le même sens. Chaque institution tend à développer sa propre culture : les parents, les élèves, les professeurs, les mathématiciens, les ingénieurs parlent avec les mêmes mots de connaissances différentes, transposées. On peut même ajouter que chacun de nous intègre plusieurs rapports différents aux mêmes objets mathématiques : à titre personnel, en tant que professeur, en tant qu’apprenants, nous utilisons des concepts, des techniques, des termes, différents et nous les ressentons différemment. Des cloisons étanches s’élèvent entre nos différents rapports et nous rendent incapables d’utiliser ce que nous savons dans certains cas. Nous pouvons même, à force de "concessions" aux possibilités de la situation, perdre complètement notre vigilance mathématique.

L’enseignement se faufile difficilement dans ce labyrinthe. D’autant plus que la plupart des partenaires croient qu’il existe "naturellement" une culture commune et des moyens "naturels" de transmission, au moins pour les connaissances "simples" de l’école primaire et qu’ils refusent de renoncer à cette illusion.

Sur les situations

Chercher les conditions d’existence d’un savoir est pourtant un moyen général de recherche en didactique. La description systématique des situations d’enseignement peut modéliser les différents rapports aux mathématiques créant — et créés par — la transposition. C’est un moyen direct pour discuter avec les enseignants ce qu’ils font ou ce qu’ils pourraient faire. Elle permet aussi de considérer comment ils pourraient pratiquement prendre en compte les résultats des recherches (en didactique et dans d’autres domaines). L’étude (et la théorie) des situations et de leurs variables didactiques apparaît donc comme un moyen privilégié de communication entre les chercheurs et les enseignants, surtout comme un outil pour l’ingénierie didactique et donc comme un moyen de créer une indispensable culture didactique commune.

Des situations aux leçons et aux processus

Nos premiers exemples laissent dans l’ombre la diversité des situations nécessaires à l’ensemble du processus, la complexité des rapports au savoir, et un grand nombre d’autres phénomènes tels que ceux que nous allons évoquer.

Il y a loin des situations "fondamentales" ci-dessus aux leçons quotidiennes dans la classe et les professeurs d’écoles doivent ordinairement gérer de nombreux paramètres. Parmi les plus importants, les rapports avec le milieu matériel, l’apprentissage du traitement social de la vérité, l’équilibre entre différents statuts des connaissances en classe, et particulièrement l’équilibre entre les connaissances et les savoirs. Nous ne parlerons pas ici du rôle essentiel de la mémoire du professeur, auxiliaire indispensable de la maîtrise du temps didactique et des apprentissages.

Le milieu, la vérité, les connaissances et les savoirs

Les rapports avec le milieu matériel

Un double assujettissement

Un enfant qui dessine une maison, représente-t-il une maison précise ou accomplit-il une activité rituelle dont les éléments symboliques lui sont fournis par son milieu culturel ?

Dans le premier cas, il prend effectivement en charge certaines relations entre son modèle et le dessin : par exemple il fait deux portes parce que sa maison a effectivement deux portes. Dans le second, il ne travaille qu’au niveau symbolique : une maison-icône ou métaphore a toujours une seule porte, deux fenêtres placées symétriquement et une cheminée … quatre fenêtres un créneau et un drapeau et voilà un château. L’assujettissement de l’élève tantôt à un milieu matériel, pris effectivement en compte, tantôt à un milieu culturel en rapport plus symbolique avec sa réalité actuelle, et surtout le passage pertinent de l’un à l’autre est une des difficultés majeures de l’enseignement primaire. Cette difficulté a été très bien mise en évidence à propos de la géométrie par D. FREGONA [2].

Est-il possible, et souhaitable de personnaliser le rapport de l’élève au milieu, aux signes et aux symboles mathématiques ?

Les objets, leurs représentations et leurs propriétés

Reprenons notre étude de l’enseignement du nombre ;

Les notions de correspondance, de caractère commun et de représentation d’un objet ou d’un concept par un dessin forment les connaissances d’entrée de la situation fondamentale du nombre. Leur apprentissage peut commencer à l’école maternelle dans des situations d’action, de formulation et de débats qui ont pour objet de les mettre en position d’actants, d’interlocuteurs et de juges.

Pour cela, nous avons proposé aux enfants de 5 ans l’activité des "trésors" : une situation où ils devaient se souvenir, l’après-midi, des objets placés dans une boîte, le matin même, devant eux. Ces petits objets étaient choisis parmi un ensemble assez important et étaient eux-mêmes assez nombreux pour que les élèves doivent en faire la liste. Et comme ils ne savaient pas écrire, ils devaient les représenter par des dessins, dans un premier temps pour les reconnaître et bientôt pour faire savoir à un camarade ce que la boîte contient. Le camarade "lisait" les signes du premier et un compère donnait la vérification immédiate : l’objet était là ou n’y était pas. La situation évoluait lentement jusqu’à la création effective des divers codes [3] par les élèves.

Les objets étaient choisis de manière appropriée pour nécessiter ou favoriser toutes sortes de modes d’identification et de représentations et nous avons pu en observer la mise en œuvre. En particulier il y avait des petits sacs de 2, 3, ou 4 billes identiques qui ne se distinguaient que par le nombre. Le premier procédé qui apparaît est la trace : les enfants décalquent le contour de l’objet à représenter. Par la suite, ils enrichissent ce dessin de caractères oppositifs ou de détails distinctifs, et utilisent des propriétés.

Certaines, comme la matière (terre ou verre pour une bille), n’ont rien de figuratif. La grenouille, beaucoup plus grande que la feuille de dessin leur pose un réel problème. L’idée d’inventer un dessin petit qui ressemble (qui présente quelques traits) à son grand modèle ne vient pas immédiatement. Mais lorsqu’un enfant résout ce problème, la plupart des autres l’imitent et tous envisagent cette "découverte" comme une conquête précieuse. À cinq ans les quatre boules sont aisément distinguées de trois, et même de cinq, avec ou sans comptage.

Ces situations dans leurs phases de débats mettent en évidence le plaisir et la capacité qu’ont les enfants de cinq ans, de choisir, de formuler et de défendre leur point de vue (sur le choix d’un signe par exemple).

Pendant toute la scolarité, l’usage effectif des nombres naturels va poser des problèmes dans les rapports avec le milieu. Par exemple, lorsqu’il s’agira d’apprendre à mesurer, il faudra ignorer les erreurs, "négliger" les approximations, pratiquer implicitement puis explicitement les encadrements, et maîtriser sans le dire la structure de l’espace mesurable utilisé’ (ici l’ensemble des parties d’un ensemble fini). Souvent les naturels ne sont utilisables qu’au mépris (justifié) du milieu.

La causalité

Pourquoi est-il intéressant et parfois vital d’anticiper sur ce qui va arriver ? Relier un fait à un autre est une capacité naturelle développée spontanément très tôt par tout humain. Mais concevoir cette relation non pas comme un effet de la contingence mais comme une conséquence nécessaire de conditions reproductibles est une conquête culturelle. Ce n’est pas si simple d’envisager qu’une chose qui, visiblement est vraie (établie comme une évidence dans une relation avec un milieu matériel par exemple), pourrait ne pas l’être, pour ensuite s’attacher à montrer qu’elle l’est nécessairement, comme conséquence logique d’autres faits établis. Cela commence à s’apprendre et à s’enseigner, au moins sous une forme appropriée, dès l’école primaire.

Le traitement personnel et social de la vérité.

L’école primaire doit permettre le développement de la personnalité rationnelle de l’élève et lui enseigner les comportements sociaux relatifs à la prise de décision et à l’établissement de la vérité et à l’utilisation des savoirs

La vérité

L’apprentissage le plus fondamental que les enfants puissent trouver dans les mathématiques à l’école primaire me semble être celui de la gestion personnelle et sociale de la vérité. Les mathématiques n’ont pas le monopole de la recherche de la vérité mais elles sont le domaine où on la rencontre le plus précocement et où on peut apprendre à la traiter avec le moins de savoirs préalables.

Quand une déclaration mathématique est-elle "vraie" ? Dans ce que l’élève accepte ou apprend, quelle est la part de ce qu’il peut constater par lui même, de ce qu’il voit avec "évidence", de ce qu’il comprend dans ses rapports avec un milieu "objectif’ ?

Comment apprend-il qu’il doit parfois changer d’avis ?

Quelle est la part de ce qu’il doit accepter ou refuser de l’opinion des autres et par quels moyens ? Comment peut il les convaincre ? Dans quelles conditions doit-il se rendre à l’opinion des autres ? Que lui apporte la culture et l’autorité du maître ? Comment une vérité s’établit-elle dans la société, comment se contrôle-t-elle, et quels avantages y a-t-il à le faire ? Quelle est la responsabilité de chacun dans ce rapport à la vérité ?

Ces questions semblent bien éloignées des ambitions de l’enseignement primaire des mathématiques, pourtant elles s’y présentent immanquablement très tôt et la façon de les traiter est d’une grande importance pour les enfants et pour la société.

La pratique du débat et la rhétorique naturelle des enfants

Il est souvent nécessaire de prévoir avec assurance, de savoir sans avoir à chercher, de comprendre pour économiser de la mémoire, de démontrer pour comprendre, de discuter pour aimer le faire, de s’étonner pour le plaisir d’interroger ses compagnons, etc.

L’éveil de l’enfant à ces pratiques, aux plaisirs et aux déboires qu’il y trouve, est pour le professeur des écoles qui y est attentif une source permanente d’émerveillement. Je crois que la plupart des enfants sont capables de raisonner et d’apprendre à raisonner très jeunes à condition de leur en donner l’occasion, à bon escient. Ils doivent pouvoir utiliser leurs forces avec une bonne efficacité, autant pour établir et comprendre la vérité que pour apprendre des savoirs nouveaux. Pour qu’ils aiment le débat et la discussion, il faut aussi leur en faire respecter les règles et les leur enseigner [4].

Le travail de l’enseignant va consister à ménager ces occasions. Ce n’est pas facile car, en tant que moyen d’action, la compréhension est toujours - localement - plus chère que l’application d’un algorithme. Pour acquérir une connaissance il parait toujours meilleur marché de l’acheter que de la refaire soi-même : la réflexion, le débat, le raisonnement et la démonstration, ou le recours à l’expérience, paraissent toujours extrêmement plus coûteux que l’emprunt des conclusions, l’application, l’étude ou l’apprentissage formel. Et c’est souvent vrai ! De plus, même bien préparés et bien menés, les débats entre élèves peuvent souvent s’enliser dans du verbiage sans objet, des "conflits" sans issue et des considérations sans intérêt, entreprises dangereuses en ce qu’elles habituent certains élèves à fuir les "vrais" débats de savoir pour de fumeux artifices.

Mais la somme de comportements économiques localement optimaux ne produit pas un processus — globalement — optimal. L’art didactique consiste à maintenir un équilibre entre des conditions opposées qui tendent à faire échouer le projet.

Les soixante lignes ci-dessus constituent un bel exemple de prêchi prêcha du genre de celui dont on nous nourrissait en formation pédagogique(J’ai eu la chance d’en avoir une à l’école normale d’Agen dans des temps désormais bien reculés) : sympathique mais totalement incantatoire.

Car, pour que cet art puisse s’exercer, il faut une bien meilleure connaissance des phénomènes qui agitent et régissent la transmission des connaissances, le plus souvent à l’insu de ses protagonistes, et des indices qui permettent de les déceler. Il faut des moyens "techniques" c’est à dire des situations effectives, spécifiques de chaque savoir, capables de déterminer les relations effectives que les élèves doivent établir et que le professeur doit ménager et gérer. Il faut à la fois une bonne connaissance - réaliste - et une représentation OPTIMISTE de ce que PEUVENT faire les enfants, de ce qu’on peut attendre d’eux.

La première expérience qui me persuada de la possibilité d’organiser des situations de débats entre les élèves de l’école primaire, à propos d’énoncés de mathématiques, portait sur la découverte de la division à propos de la "course à vingt". Il y en a eu beaucoup d’autres depuis.

La démonstration et la preuve

En tant que pratique sociale, la preuve est le moyen légitime de convaincre un interlocuteur : un tel moyen doit respecter l’interlocuteur en utilisant seulement son répertoire et les informations dont il dispose, lui, actuellement (répertoire logique, mathématique, scientifique …), et il doit exclure tous les autres moyens de pression, rhétoriques (habileté formelle), psychologiques (tels que la séduction, l’autorité, l’apitoiement) ou contrainte matérielle (menace, violence, etc.).

La pratique de la preuve se construit contre toute une série de barrières psychologiques, culturelles ou sociales telles que l’amour propre, l’instinct grégaire ou la fidélité … L’instrument de cette initiation est l’apprentissage de la démonstration, non pas (seulement) comme savoir officiel mais comme moyen courant de pratiquer la preuve (et de la limiter à son domaine de pertinence).

Elle est fondatrice de l’individu, et particulièrement de l’individu rationnel, tout autant que des rapports sociaux les plus essentiels. Il ne peut pas y avoir de démocratie sans une organisation sociale qui intègre le rôle de la connaissance dans la décision et sans une gestion commune et correcte du savoir, de la vérité et de la preuve.

À l’école primaire, cette formation civique fondamentale ne se formule pas, mais elle se fait aussi et peut être d’abord en mathématiques.

Les connaissances et les savoirs

Quelle est la place de ce que l’élève comprend, de ce qu’il apprend lui même, de ce qu’on lui suggère ou qu’on lui enseigne et de ce qu’il étudie dans ce qu’il sait ?

Résoudre un problème ou connaître une théorie mathématique mobilise un amalgame complexe de connaissances et de savoirs. Distinguons-en deux, pour simplifier, et appelons "connaissances" les ressources et les moyens, souvent implicites et complexes, développés plus ou moins spontanément, pour répondre aux exigences du milieu (par exemple on connaît son quartier, on reconnaît ses voisins sans pouvoir dire exactement comment). Ces connaissances sont mises en œuvre par un élève dans la résolution des problèmes pour solliciter et organiser les formes explicites et institutionnellement acceptables qui constituent la solution. Appelons "savoirs" ces formes, techniques et concepts (par exemple, savoir que les diagonales d’un rectangle sont égales). Ils sont produits par les institutions, et destinés à permettre le repérage, la reproduction, le contrôle, la justification et la diffusion des connaissances. Les connaissances ne sont pas la conversion, loin s’en faut, des savoirs utilisés officiellement pour la correction du problème, elles ne peuvent donc pas non plus se convertir directement en savoirs.

L’usage et l’apprentissage des savoirs exige toujours la présence de connaissances relatives à la notion enseignée (mais aussi à d’autres). Le professeur s’attend à ce que l’élève convertisse les savoirs qu’il lui enseigne en moyens de résolution des problèmes qu’il lui pose, et inversement à ce qu’il convertisse en savoirs, des connaissances qu’il considère comme cachées mais accessibles dans ses exercices.

Au cours de l’enseignement, les notions glissent d’un statut à un autre, mais à chaque instant le professeur ne peut en isoler une et la traiter avec un statut unique. Il gère ainsi un ensemble de notions dont quelques unes seulement peuvent être explicitement traitées.

À l’école primaire, la part des connaissances indicibles mais nécessaires est particulièrement importante et délicate et la gestion de leurs rapports avec les savoirs enseignés ne l’est pas moins.

L’enseignement de la géométrie dans la scolarité obligatoire offre des exemples typiques des difficultés à développer de façon harmonieuse la connaissance de l’espace et les savoirs de géométrie, ainsi que l’ont montré R. BERTHELOT et M. H. SALIN [5].

Dans les passages d’un niveau scolaire à un autre, il est souvent impossible pour l’enseignant du niveau supérieur d’utiliser les connaissances, pourtant acquises par ses élèves au niveau précédent, mais non converties en savoirs évaluables (impossibilité due au fait, entre autres, que l’enseignant ignore ou est sensé ignorer les situations, les exercices et les méthodes utilisées par son prédécesseur, due à l’absence de culture commune, ou à un goût prononcé pour les "questions vierges" ou supposées telles). En conséquence, les connaissances mal gérées perturbent les apprentissages ultérieurs, de nombreux savoirs "fonctionnent" mal, et la progression est ralentie [6].

Du côté des enseignants

Mais les enseignants ne peuvent ils pas directement coordonner leur action ? Les experts et les responsables ne peuvent-ils pas déterminer ce qui doit se faire ?

Un accident de transposition

Pour illustrer ce qu’est l’enseignement des mathématiques à l’école primaire du côté des professeurs je vous propose d’examiner un problème de transposition.

Un document "épouvantable"

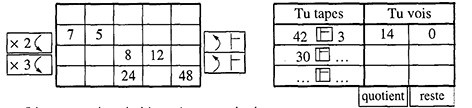
Une collègue nous a récemment apporté un journal professionnel d’enseignants qui présentait un document étonnant. L’auteur y vantait l’usage d’une calculatrice pour enseigner et "comprendre un concept délicat à acquérir : la proportionnalité". Il présentait d’abord un tableau de nombres naturels à compléter en effectuant des opérations (multiplications et divisions par 2 et 3) communes à tous les nombres d’une même ligne (Exercice classique, à gauche sur la figure). Il invitait ensuite les élèves à utiliser la touche "division euclidienne" par trois, pour retrouver les nombres de la ligne supérieure qu’ils venaient de multiplier par trois (tableau de gauche). Grâce à cette touche, cette calculette spéciale affiche, non pas l’approximation décimale du quotient rationnel (comme ordinairement avec la touche "division"), mais le quotient naturel et le reste de la division (aménagement didactique qui évite l’intrusion des décimaux avant terme et dont il faut remercier le constructeur). Evidemment tous les restes sont nuls.

L’auteur, qui avait étiqueté cette opération :
"pour vérifier la proportionnalité des nombres entre les lignes 3 et 2, utilise la touche division euclidienne …",
conclut ainsi :
"quand le reste est égal à 0, les deux nombres sont proportionnels (! c’est moi qui souligne). Le coefficient de proportionnalité est indiqué par le quotient !"

L’exercice continue par un nouveau tableau où les nombres de la colonne de gauche doivent être divisés (avec la machine) par les nombres de la deuxième colonne, tous différents. Les restes et les quotients doivent être simplement transcrits dans les colonnes trois et quatre.

"Colorie les coefficients de proportionnalités quand les nombres sont proportionnels"
continue l’auteur qui enfonce le clou avec la "leçon" suivante :
"Pour (vérifier si des nombres sont proportionnels) il suffit de les entrer sous la forme de fractions. Si la fraction est entièrement simplifiable, les deux nombres sont proportionnels, le plus grand sera le numérateur. Plusieurs appuis successifs sur la touche "SIMP" montrent lorsque l’on obtient un nombre entier :

• a) que les nombres sont proportionnels
• b) le coefficient de proportionnalité"

Son corrigé (partiel)

Les termes "proportionnel", "proportionnalité" et "coefficient de proportionnalité" ne sont pas employés ici conformément aux usages mathématiques.

L’auteur utilise "proportionnel" comme adjectif s’appliquant à deux nombres (or "proportionnel" veut dire "relatif à une proportion" ou qui est "déterminé par une proportion", et pour définir une proportion il faut quatre nombres a ; b ; c ; d ; tels que a/b = c/d). Et il l’utilise pour indiquer que l’un des deux nombres, (peu importe lequel) est multiple de l’autre (qui en est un sous multiple). De plus la suite montre qu’il utilise le terme "coefficient de proportionnalité" pour désigner alors le rapport de deux nombres lorsqu’il est entier naturel — il devient alors simplement synonyme de quotient (entier). En fait le coefficient de proportionnalité entre les colonnes un et deux n’est pas le quotient — différent sur chaque ligne — ni même le nombre 3, par lequel on divise toujours (c’était coefficient pour la troisième ligne en fonction de la deuxième), c’est 1/3 ou 0,333 …

Sans changer les exercices il aurait pu dire :
"Pour vérifier la proportionnalité des deux suites de nombres des lignes 3 et 2, utilise la touche division euclidienne. En divisant tous les nombres de la troisième ligne par 3, tous les quotients sont le nombre correspondant de la deuxième et tous les restes sont égaux à 0.
L’évocation de la proportionnalité n’a pas grand intérêt :
Les deux lignes sont proportionnelles. et dans ce cas "3" est le coefficient de proportionnalité de la troisième ligne en fonction de (ou par rapport à) la deuxième …"

puis plus loin :
"colorie les quotients quand le premier nombre est un multiple (ou multiple exact) du second, Si tous les quotients sont égaux et si tous les restes sont nuls alors la suite des premiers nombres est proportionnelle à la suite des seconds et le quotient commun est le coefficient de proportionnalité."

Critique

Ce que les élèves ont à faire est raisonnable, et on peut soupçonner ce que le professeur a pu vouloir enseigner : pour vérifier que deux suites de nombres (naturels) sont proportionnelles (un des coefficients de proportionnalité étant naturel), il faut que la division des plus grands par ce coefficient donne des restes nuls.

Ne s’agit-il donc que d’une erreur de vocabulaire, une formulation contraire aux usages mais qu’il suffira de rectifier ? Ne pouvons nous laisser à plus tard l’apprentissage de la précision verbale et des savoirs "formels" pour ne s’attacher qu’aux connaissances ? La réponse est NON. D’abord cette formulation est incohérente car les enfants pourront appeler "tableau de nombres proportionnels" un tableau mettant en correspondance les nombres d’une première colonne avec, dans une deuxième colonne, des multiples quelconques mais surtout variés, des premiers. Chaque ligne déterminera un (soi disant) "coefficient de proportionnalité" différent et le tableau de nombres soi-disant proportionnels ne sera pas un tableau de proportionnalité !

De plus cette confusion conduit à confondre aussi et à échanger les rôles des termes d’un produit. Si a x b = c, alors a et b sont tous les deux des "coefficients de proportionnalité" ! Et l’auteur n’évite pas l’erreur : ce sont les valeurs de la deuxième ligne ( ou de la 3°’ colonne) qui deviennent des coefficients de proportionnalité !

L’erreur se révélera catastrophique dès l’apparition des nombres rationnels et des nombres décimaux car alors tous les nombres seront "proportionnels" … Il y a bien d’autres inconvénients, la cause est entendue : la précision et l’exactitude formelle ne sont pas un luxe imposé arbitrairement par des puristes doctrinaires. Il faut des mots pour penser et dire les choses, et leur choix quand il résulte d’une culture ancienne et concertée n’est ni innocent ni facile à remettre en cause.

Une explication

Essayons de comprendre d’abord l’origine du pataquès.

Il est clair que les formulations "correctes" sont un peu plus délicates et les phrases plus longues. Le mot "suite" est difficile à éviter et "tous", impossible. On peut comprendre qu’un enseignant se laisse aller, pour coller au répertoire de ses élèves à quelques abus, mais je sais aussi qu’il est possible de présenter ces tâches aux élèves, sans abus de langage, et sans que le vocabulaire nécessaire présente pour eux de grandes difficultés. Personne n’est obligé d’émettre de grandes phrases en forme de théorèmes comme tente de le faire notre auteur mais les caractéristiques d’un tableau de proportionnalité par rapport à un tableau quelconque peuvent être parfaitement connues des élèves. Alors que se passe-t-il ? Avons-nous affaire simplement à un cuistre qui commet une bêtise isolée ?

Un rapide raisonnement de didactique fait pressentir que non. Cette erreur est du type de celles que peuvent commettre en situation de nombreux enseignants, même s’ils sont eux même bien informés des mots et de leur sens. Une enquête impromptue a confirmé ce raisonnement. Et pour finir, plus de 90% des candidats au concours externe de recrutement des professeurs des écoles, à la critique desquels la feuille a été proposée, ne lui ont rien trouvé à redire !

Faut-il s’écrier encore "Ah que le niveau baisse mon cher !" et penser que lorsque 200 000 instituteurs font la même faute, c’est évidemment parce qu’il y a là 200 000 sots ?

Sans examiner en détail les mécanismes didactiques qui rendent probables de telles aberrations, il faut remarquer le plus important : certains usages de la langue française ne coïncident pas avec les usages mathématiques (par exemple le mot "proportion" y est souvent synonyme de "rapport" : les proportions d’un modèle). À l’école primaire de tels conflits sont très difficiles à arbitrer. Les enseignants ne peuvent le faire qu’avec l’aide de conventions précises et la complicité de toute la société.

Les effets des réformes

Mais il me semble que cet exemple montre aussi les conséquences d’un important phénomène de transposition didactique. Dans les années 70, un souci légitime d’unification du langage mathématique et d’amélioration du niveau des élèves, a conduit à éliminer des programmes du secondaire la théorie des proportions et plus généralement à abandonner une partie de sa fonction, qui consistait à donner une place épistémologique et des instruments d’analyse pour les connaissances du primaire.

Dans le primaire, les problèmes de proportionnalité ont dû être "reconditionnés" et la notion d’application linéaire est venue remplacer la règle de trois (présentation sous forme de tableaux par ex.). Les termes "rapport" et "multiple" ont perdu leur usage et leur sens précis, à la fois pour les professeurs d’écoles qui ne disposaient que des mathématiques du premier cycle, et pour les élèves du primaire.

Mais avant qu’une "culture professionnelle" nouvelle ait pu s’établir, une nouvelle réforme a supprimé des programmes les concepts et le vocabulaire (des ensembles et des relations par ex. mais aussi les termes de rapports, de multiple etc.) qui devaient permettre aux professeurs de maîtriser progressivement ces difficultés et de créer les instruments et les exercices nécessaires. Les exercices et les tableaux sont restés mais pas les termes pour les traiter.

Aujourd’hui, les à-coups imposés à l’enseignement par des décisions empiriques et doctrinaires ont mis à mal même la communication des concepts les plus simples.

Les chercheurs en didactique mettent en évidence ces phénomènes et leurs causes. Les formateurs de professeurs tentent d’utiliser ces connaissances pour corriger les aspects les conséquences les plus négatives de ces improvisations. La décision de supprimer tout "ce qui passe mal" associée à la volonté opiniâtre de conserver une gestion empirique et administrative des savoirs finira par ne plus rien laisser passer. Il faut préserver les concepts fondamentaux, les mots nécessaires pour les utiliser, les exercices pour les apprendre, les situations qui leur donnent du sens.

Du côté de la société

La noosphère

Ce ne sont pas seulement les réformes ou le manque de réformes qui sont en cause, ni les grands coups de volants idéologiques dans tous les sens que nous nous sommes permis dans une période faste pour notre culture et pour notre économie. C’est la conception même des moyens de gestion de l’enseignement primaire qui est en cause. Comme pour l’économie au XVIII^e siècle, nous commençons à peine à soupçonner les lois profondes de la diffusion des savoirs, et comme au XIX^e siècle, nous croyons qu’il suffit de dire à chacun ce qui le menace ou qui l’opprime pour qu’il s’organise pour y résister. Même les meilleures intentions peuvent paver l’enfer de l’enseignement.

L’intérêt des mathématiciens, et surtout des plus grands, pour l’enseignement élémentaire, est indispensable. Il a été constant en France au moins depuis la fin du XVIII^e siècle. Mais il entraîne bien vite une forte probabilité de voir apparaître des critiques directes, péremptoires et inadaptées, à tout moment, à propos de tout sujet d’enseignement et de tout niveau scolaire, venant de personnes ou d’institutions diverses, à l’abri de toute rétroaction. Rien de tel pour désarmer le sentiment de compétence des enseignants dans le domaine mathématique, pour la faire rechercher ailleurs, pour infantiliser les rapports avec l’administration, avec ces institutions, avec les parents et finalement avec les élèves. Loin de moi l’idée de reconstituer la citadelle de l’enseignement primaire et les cloisonnements que nous avons connus au début du siècle, mais la culture commune ça ne se décrète pas : ça se construit, ça s’étudie, ça se débat, ça se protège, ça se maintient à l’écart des errances idéologiques trop désordonnées. Or l’enseignement constitue encore un domaine où chacun pense être suffisamment connaisseur pour pouvoir tout juger (c’est légitime) mais sans rien savoir de plus. Cela ouvre des perspectives à l’empirisme et au volontarisme (pour les politiciens, pour les mathématiciens, pour les parents et certainement pour les professeurs d’abord) pour agiter tous les fantasmes et proposer impunément toutes les réformes.

Les rapports au savoir, et surtout les rapports au savoir mathématique de la population ne sont pas encore actuellement gérés par des institutions adéquates. L’enseignement obligatoire va souffrir longtemps encore de cette absence.

Quand les nombres se démasquent

Les connaissances mathématiques de l’école primaire apparaissent souvent comme une base nécessaire, un peu sommaire mais, solide, universelle, et en un certain sens "vraies".

J’ai manqué de temps pour donner à mon texte une forme plus agréable et surtout à mes propos, tous les arguments et les exemples concrets qui seraient nécessaires. J’aurais voulu montrer aussi la nécessité et la possibilité de maintenir un enseignement des structures, d’un vocabulaire adéquat, et d’un minimum de métaconcepts et de métalangage.

Il aurait été surtout utile de montrer que l’enseignement obligatoire ne peut pas obéir à la vision naïve que s’en fait aujourd’hui l’opinion publique. Les savoirs de la scolarité primaire (et a fortiori obligatoire) ne peuvent pas être enseignés comme des savoirs définitifs, ou seulement à compléter et peut-être un peu à reprendre, mais plus tard.

L’existence des obstacles épistémologiques le prouve. La connaissance des naturels s’érige en obstacle à l’apprentissage des rationnels mais surtout des décimaux. Le fait est maintenant bien connu et la liste des erreurs qui lui sont imputables est bien établie (dissociation 0,3 x 0,3 = 0,9 ou 4,8 x 4,8 = 16,64, "multiplier doit agrandir alors on ne comprend pas x 0,8" ; etc.).

C’est un cas particulier des obstacles dus au plongement d’une structure dans une autre. Voici qu’une extension (ou une adjonction, une symétrisation, une complétion ou toute autre sorte de complexification) met à votre disposition des outils nouveaux pour résoudre plus aisément des problèmes jusque là difficilement accessibles et heureusement vos anciens outils sont toujours là, encore disponibles et inclus dans la nouvelle structure, mais sous le masque familier un étranger se profile et l’élève non averti refuse l’extension ou renonce à comprendre.œœœ

Voici le bon nombre "4" que l’enfant "connaît" bien par ses propriétés particulières (j’allais dire "personnelles") et son écriture. Il n’a déjà pas trop pu se faire à l’idée que 3 + 1 est aussi 4, pour lui c’est différent mais "ça fait 4" grâce à une opération bien connue. Si quatre a un rapport avec quelque autre nombre, c’est bien avec ses voisins : son prédécesseur, 3 et son successeur 5.

Or, voici que quatre peut changer de visage : 4,00 ou même 4,000000 … Si je divise 12 par 3 et que je pousse indéfiniment. Il n’a plus ni prédécesseur ni successeur …On peut même ne plus le reconnaître du tout "3,99999 …" si on prend 4 qu’on le divise par 3 puis qu’on le multiplie à nouveau par 3, on a perdu un petit bout ou non ?

L’enseignement primaire fuit de plus en plus ces dilemmes et renonce à avouer aux élèves qu’il faut apprendre des savoirs provisoires, puis les réviser et les modifier. Il renonce surtout à dire à la société qu’elle doit bien enseigner des savoirs provisoires, justes dans leur environnement mais certainement faux ailleurs et que les fautes qui en découlent sont légitimes, ou en tout cas acceptables dans la mesure ou elles seront révisées et enseignées comme révisables. Le seul moyen d’apprendre un savoir non révisable serait d’apprendre par cœur "le" texte de ce savoir (et si possible de ne pas s’en servir) Existe-t-il un tel savoir ?

Pourquoi cacher les difficultés aux enfants ? Et ne pas montrer l’intérêt des connaissances, des techniques et des savoirs ?

La culture mathématique du public

II y a cinquante ans, l’école "primaire", avec ses prolongements post et périscolaires, ses cours complémentaires et ses préparations diverses, assurait, outre la formation générale de l’ensemble de la population, une grande partie, dite "théorique", de la formation professionnelle de nombreux métiers. Cette activité protéïforme présentait bien des inconvénients qui ont conduit à sa réduction progressive. Mais elle donnait à son enseignement des mathématiques un vaste cadre d’applications de toutes sortes et à ses contenus une légitimité indiscutable. Je me souviens avec émotion du jour où mes parents m’ont acheté le petit mémento Larousse, et de l’enchantement qui m’a saisi lorsque j’ai vu que je comprenais tout ce qui y était écrit et que je savais faire tous les problèmes. Mon père m’apprit à extraire les racines carrées qui n’étaient pas dans le livre. J’avais dix ans et je pensais que je n’avais plus rien à apprendre. J’entrepris alors avec confiance de me mesurer à un ouvrage que je découvris chez une tante : 4837 problèmes classés pour préparer le CEP ! Quelle ivresse de découvrir la quantité de questions utiles auxquelles je savais répondre. Je ne tardais pas à en chercher moi même de nouvelles. C’est aussi cela les mathématiques de la scolarité obligatoire, un certain champ à cultiver avec quelques outils et des marges à découvrir. Je me souviens aussi de la joie que j’ai éprouvé un peu plus tard à reprendre ce champ à l’aide de l’algèbre.

Il ne semble pas qu’aujourd’hui l’enseignement primaire détermine et reconnaisse un tel champ d’application. Cela ne facilite pas l’identification d’une culture, aussi bien pour les élèves que le public. Ne serait-il pas possible, sans reproduire les erreurs de ségrégation de la triple culture (primaire, secondaire, supérieure), de ponctuer plus explicitement les progrès des connaissances et de leurs champs d’application ? Mais cela aussi supposerait une modification de la culture mathématique du public …

Connaître et gérer l’enseignement obligatoire est la responsabilité de la société tout entière et non celle d’une minorité de "prêtres". Mais pour gérer les exigences et les indulgences de la culture il faut des instruments culturels et sociaux.