1. Expression de cos n\(\alpha\) en fonction de cos \(\alpha\)

Théorème 1

Pour tout entier naturel n, cos n\(\alpha\) s’exprime en fonction de cos \(\alpha\) sous forme d’un polynôme \(T_n (\cos \alpha)\).

Nous avons cos 0\(\alpha\) = 1, cos 1\(\alpha\) = cos \(\alpha\), cos 2\(\alpha\) = 2 cos 2\(\alpha\) - 1 et, de façon un peu
moins évidente, cos 3\(\alpha\) = 4 \(\cos^3 \alpha\) - 3 cos \(\alpha\).
En outre, de la formule cos (n + 1)\(\alpha\) + cos (n – 1)\(\alpha\) = 2 cos \(\alpha\) cos n\(\alpha\), on tire

$$\cos (n + 1)\alpha = 2 \cos \alpha \cos {n}\alpha - \cos ({n} – 1)\alpha.$$

On en déduit une méthode de calcul de cos n\(\alpha\) sous forme d’un polynôme en cos \(\alpha\). Plus précisément, si l’on définit une suite de polynômes \(T_n\) par : \(T_0(x) = 1, T_1 (x) = x\) et, pour n ≥ 2, \(T_{n+1} (x) = 2xT_n (x) – T_{n-1} (x)\), on voit aussitôt par récurrence que, pour tout n, l’on a \(\cos n\alpha = T_n (cos \alpha)\).

Propriétés élémentaires de \(T_n\)

Les polynômes sont les polynômes de Tchebychev [1] . Contentons-nous ici d’en donner les seules propriétés qui vont nous servir.

Les premiers de ces polynômes, outre \(T_0\) et \(T_1\) , sont : \(T_2 (x) = 2x^2 - 1\), \(T_3 (x) = 4x^3 - 3x\), \(T_4 (x) = 8x^4 - 8x^2 + 1\).
Les points suivants sont immédiats par récurrence :

• Les coefficients de \(T_n\) sont des entiers relatifs.
• \(T_n\) est de degré n.
• Le coefficient de \(x^n\) dans l’écriture de \(T_n\) est \(2^{ n-1}\) .
• Le terme constant de \(T_n\) est nul pour n impair.

2. Angles rationnels à cosinus, sinus ou tangente rationnels

Théorème 2

Les seules valeurs rationnelles que puisse prendre le cosinus ou le sinus d’un angle rationnel sont 0 , 1 , -1, \(\frac{1}{2}\) et \(-\frac{1}{2}\).

Notons d’abord que si l’angle \(\alpha\) est rationnel, l’angle \(\frac{\pi}{2}-\alpha\) l’est aussi. Il suffit donc de faire la démonstration pour le cosinus.
Si \(\alpha\) est multiple de \(\frac{\pi}{2}\), cos \(\alpha\) vaut 0, 1 ou -1. On écarte désormais ce cas. Soit donc un angle rationnel \(\alpha=\pi \frac{k}{n}\), où k et n sont des entiers premiers entre eux, n étant supérieur à 2.

Premier cas : n impair

Supposons donc que cos \(\alpha\) soit rationnel et posons cos \(\alpha=\frac{u}{v}\), où u et v sont des entiers premiers entre eux (v > 0). Nous avons cos \(n\alpha=(-1)^k\) . Écrivons explicitement \(T_n(\frac{u}{v})\), en n’oubliant pas que son terme constant est nul [2] :

$$T_n \left( \frac{u}{v} \right)=2^{n-1}\left( \frac{u}{v}\right) ^n+\dots+c_{n-j}\left( \frac{u}{v}\right) ^{n-j}+\dots+c_1\frac{u}{v}$$

où les \(c_j\) sont des entiers relatifs. L’égalité \(T_n \left( \frac{u}{v} \right)= (-1)^k\) donne :

$$2^{n-1}u^n+\dots+c_{n-j}u^{n-j}v^j+\dots+c_1uv^{n-1}=(-1)^kv^n$$

L’entier relatif u divise le premier membre, donc aussi le second ; mais il est premier avec v, donc il ne peut valoir que 1 ou -1. De même v divise tous les termes de l’égalité ci-dessus autres que le premier, donc il divise aussi celui-ci, c’est-à-dire \(2^{n-1}u^n\) et, comme il est premier avec u, il divise \(2^{n-1}\).

La valeur de cos \(\alpha\) est donc du type \(\frac{\varepsilon}{2^r}\) avec \(\varepsilon=\pm 1\) et r entier positif ou nul.

Si r = 0, on retrouve les solutions triviales cos \(\alpha= \pm 1\), déjà écartées ;
si r = 1, on obtient cos \(\alpha= \pm \frac{1}{2}\) , avec \(\alpha=\pm \frac{\pi}{3}\) ou avec \(\alpha=\pm \frac{2\pi}{3}\) modulo \(2\pi\).

Supposons maintenant r ≥ 2. Puisque cos 2\(\alpha=2cos^2 \alpha-1\), le cosinus de l’angle \(2\alpha=\pi\frac{2k}{n}\) est rationnel. D’après ce que l’on vient de prouver, ce cosinus est de la forme \(\frac{\varepsilon’}{2^s}\), avec \(\varepsilon=\pm 1\) et s entier positif ou nul.

On a donc \(\frac{\varepsilon’}{2^s}=\frac{\varepsilon}{2^{2r-1}}-1\) . Le second membre est compris entre \(\frac{1}{8}-1\) et \(-\frac{1}{8}-1\),
c’est-à-dire entre \(-\frac{9}{8}\) et \(-\frac{7}{8}\). Cela impose \(\varepsilon’=-1\) et s=0, mais alors le premier membre vaudrait -1, ce que ne saurait valoir le second. Le cas r ≥ 2 ne peut donc pas se présenter.

Second cas : n pair non multiple de 4.

Supposons donc \(\alpha=\pi\frac{k}{2m}\) où k et m sont des entiers premiers entre eux, et cos \(\alpha\) rationnel. Puisque cos \(\alpha\) est rationnel, cos 2\(\alpha\) l’est aussi. Mais 2\(\alpha\) satisfait aux
hypothèses du premier cas, donc vaut 1 , -1, \(\frac{1}{2}\) ou \(-\frac{1}{2}\).

De cos 2\(\alpha=2\cos^2 \alpha\) -1, on déduit que les seules valeurs a priori possibles pour cos \(\alpha\) sont 1, -1, 0, \(\pm \frac{\sqrt 3}{2}\), \(\pm \frac{1}{2}\). Parmi ces valeurs, la seule compatible avec la forme
de \(\alpha\) est 0, ce qui implique n=2.

Troisième cas : n multiple de 4

Supposons maintenant \(\alpha=\pi\frac{k}{4m}\) avec k impair, et cos \(\alpha\) rationnel ; alors cos m\(\alpha\) l’est aussi. Mais \(m\alpha=\frac{k\pi}{4}\) ce qui entraîne cos \(m\alpha=\pm \frac{1}{\sqrt 2}\) contradictoire avec l’hypothèse.

Théorème 3

Les seules valeurs rationnelles que puisse prendre la tangente d’un angle rationnel sont 0 , 1 , -1.

Soit \(\alpha\) un angle rationnel à tangente rationnelle. De cos 2\(\alpha=\frac{1-\tan^2 \alpha}{1+\tan^2 \alpha}\) on déduit que cos 2\(\alpha\) est rationnel ; il vaut donc 0, 1, -1, \(\frac{1}{2}\) ou \(-\frac{1}{2}\) .

Et comme \(tan^2 \alpha=\frac{1-\cos 2\alpha}{1+\cos 2\alpha}\), les valeurs à examiner pour tan \(\alpha\)sont ±1, 0, \(\frac{1}{\sqrt 3}, \pm \sqrt 3\). En écartant les valeurs irrationnelles, restent 0, 1 et -1.
N.B. : à ces valeurs, il est naturel d’ajouter \(\infty\) … ne serait-ce que parce que son inverse est rationnel !

Applications géométriques

Triangles dont les trois côtés ont des longueurs entières

Soit T un tel triangle. La formule \(a^2=b^2+c^2-2cos \widehat A\), avec les notations traditionnelles, montre que tous ses angles ont un cosinus rationnel. Si un des angles, par exemple \(\widehat A\), est rationnel, son cosinus est, d’après le théorème 2, l’un des nombres 0, 1, -1, \(\frac{1}{2}\) ou \(-\frac{1}{2}\). \(\widehat A\) vaut donc \(\frac{\pi}{2}, \frac{\pi}{3}\) ou \(\frac{2\pi}{3}\) . Il en est de même pour \(\widehat B\) et \(\widehat C\).

Ainsi, tout triangle non aplati dont les côtés sont entiers et les angles rationnels est équilatéral.

En revanche, on peut aisément exhiber des triangles à côtés entiers ayant un seul angle rationnel (forcément égal à \(\frac{\pi}{2}, \frac{\pi}{3}\) ou \(\frac{2\pi}{3}\)). Si a, b, c désignent les longueurs des trois côtés, il faut et il suffit, pour que l’angle \(\widehat A\) soit rationnel, qu’ils vérifient l’une ou l’autre des trois équations diophantiennes :

$$a^2= b^2 + c^2 , a^2 = b^2 + c^2 - bc, a^2 = b^2 + c^2 + bc.$$

Donnons pour chacune un triplet solution : (5, 4, 3) ; (7, 8, 3) ; (7, 5, 3). La première de ces équations est classique [3]. Les deux autres s’écrivent, avec \(\varepsilon\)= ±1, \(4a^2=(2b+\varepsilon c)^2+3c^2\) donc se ramènent à l’équation un peu moins classique \(X^2 + Y^2 = 3Z^2\) (voir l’appendice).
Remarque

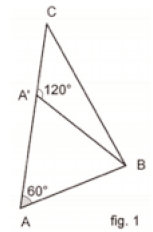
Les triangles à côtés entiers ayant un angle égal à \(\frac{2\pi}{3}\) se déduisent de ceux ayant un angle égal à \(\frac{\pi}{3}\) (et vice-versa) par une construction très simple.
Donnons-nous en effet un triangle ABC à côtés entiers tels que \(\widehat BAC=\frac{\pi}{3}\) ; on suppose qu’il n’est pas équilatéral, avec par exemple AB < AC. Prenons sur le segment [AC] le point A’ tel que AA’ = AB. Le triangle AA’B est équilatéral et donc \(\widehat BA’C=\frac{2\pi}{3}\) ; de plus le triangle A’BC a manifestement tous ses côtés entiers.

En reprenant la construction en sens inverse, on voit de même qu’à partir d’un triangle à côtés entiers ayant un angle de \(\frac{2\pi}{3}\), on peut en fabriquer un autre ayant un angle de \(\frac{\pi}{3}\) .

Triangles dont les trois sommets ont des coordonnées entières

Nous supposons dans tout ce qui suit le plan muni d’un repère orthonormal. Un point ou un vecteur sera dit entier si ses coordonnées sont entières.
Étant donné deux vecteurs entiers \(\vec V(x,y)\) et \(\vec W(x’,y’)\), l’angle orienté \(\theta\) de ces deux vecteurs vérifie la formule

$$\tan \theta=\frac{\| \vec V \| \| \vec W \| \sin\theta}{\| \vec V \| \| \vec W \| \cos\theta}=\frac{det(\vec V,\vec W)}{\vec V \cdot \vec W}=\frac{xy’-yx’}{xx’+yy’}$$

Cette tangente est donc rationnelle (à condition de considérer qu’une tangente infinie est rationnelle). D’après le théorème 3, \(\theta\) ne peut être rationnel que si cet angle est multiple de \(\frac{\pi}{4}\).

Soit maintenant un triangle dont les trois sommets sont entiers. Les seuls angles rationnels possibles pour un tel triangle sont \(\frac{\pi}{4}, \frac{\pi}{2}\) et \(\frac{3\pi}{4}\).

Un triangle aux sommets entiers ne peut avoir tous ses angles rationnels que s’il est rectangle isocèle.

N.B. : En revanche, on peut aisément trouver des triangles à sommets entiers ayant un seul angle rationnel. Un exercice intéressant est de les trouver tous.
Donnons quelques indications à ce propos.

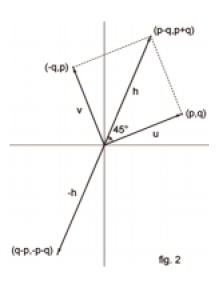
On part de l’idée suivante : étant donné
un vecteur \(\vec u\) de coordonnées (p,q), le vecteur \(\vec v\) (-q,p) s’en déduit par rotation de +\(\frac{\pi}{2}\). Le vecteur \(\vec h=\vec u+\vec v\), de coordonnées (p-q , q+p), fait avec \(\vec u\) l’angle +\(\frac{\pi}{4}\) et le vecteur \(-\vec h\) fait avec \(\vec u\) l’angle +\(-\frac{3\pi}{4}\)

Cherchons par exemple tous les triangles à sommets entiers ayant un angle de \(\frac{\pi}{4}\). On peut toujours supposer par translation que le
sommet correspondant est l’origine O. On nomme A et B les deux autres sommets, de sorte que le triangle OAB soit de sens direct.
Soit (x,y) les coordonnées de A et \(\lambda\) le pgcd des entiers x et y ; on a donc \(x=\lambda p\), \(y =\lambda q\), où p et q sont des entiers relatifs premiers entre eux. Alors le vecteur \(\vec {OB}\) est colinéaire au vecteur \(\vec h\) (p-q,q+p) et de même sens. Le pgcd de p-q et q+p est 1 si p et q sont de parité différente et 2 s’ils sont impairs tous les deux. Donc les coordonnées de B sont du type \(( \mu(p-q,q+p))\), où \(\mu\) est strictement positif, entier si et p et q sont de parité différente et multiple de \(\frac{1}{2}\) s’ils sont impairs tous les deux.

Inversement, si on se donne p et q entiers relatifs premiers entre eux,
\(\lambda\) entier strictement positif, \(\mu\) strictement positif, entier si p et q sont de parité différente et multiples de \(\frac{1}{2}\) s’ils sont impairs tous les deux, on voit immédiatement que les points O, A \((\lambda p, \lambda q)\) et B\((\mu(p-q), \mu(q+p))\) forment un triangle solution.

Polygones réguliers à sommets entiers

Soit un n-gone régulier \(A_1A_2 \dots A_n\) dont tous les sommets sont entiers. L’angle \(\widehat {A_1A_2A_3}\) vaut \(\pi \left( 1-\frac{2}{n} \right)\), les deux autres angles de ce triangle isocèle valent \(\frac{\pi}{n}\). Ce triangle à sommets entiers a donc tous ses angles rationnels ; d’après le paragraphe précédent, il est rectangle isocèle. Notre polygone est donc forcément un carré.

Il n’y a donc pas d’autres polygones réguliers à sommets entiers que des carrés.

Pour fabriquer un carré à sommets entiers, on peut toujours supposer que l’un des sommets est O. Fixons-nous arbitrairement un point A (a, b). Le carré OABC construit dans le sens direct à partir du côté [OA] est entier : le point C, déduit de A par rotation de \(\frac{\pi}{2}\) , est (-b, a) et, par \(\vec{OB}=\vec{OA}+\vec{OC}\) , on a B = (a-b, a+b).

Appendice : résolution dans \(\mathbb Z\) de \(X^2 = Y^2 + 3Z^2\)

Observons d’abord que si l’on connaît une solution (X,Y,Z), on en obtient d’autres en changeant le signe de l’un des trois nombres.

Raisonnons d’abord par conditions nécessaires.

Soit (X,Y,Z) un triplet solution et supposons, ce qui n’est pas restrictif, Z > 0. Le triplet vérifie \((X + Y) (X - Y) = 3Z^2\) ; en posant

$$X + Y = U, X - Y = V,$$

il vient \(UV = 3Z^2\) . L’un des deux nombres U et V est multiple de 3 ; il n’est pas restrictif non plus de supposer que ce soit U (intervertir U et V revient à changer Y en -Y). Posons alors U = 3W. Nous avons donc \(VW = Z^2\).

Désignons par \(\lambda\) le PGCD de V et W. Il résulte de \(VW = Z^2\) que \(\lambda^2\) divise \(Z^2\), donc que \(\lambda\) divise Z. Si l’on pose V =\(\lambda\)v, W =\(\lambda\)w, Z =\(\lambda\)vz, le triplet (v,w,z) vérifie les conditions

$$vw = z^2 \text{ et PGCD}(v,w) = 1.$$

En considérant la décomposition de \(z^2\) en facteurs premiers, on voit qu’il existe deux entiers naturels p et q tels que :

$$v =\varepsilon p^2 , w=\varepsilon q^2 , z = pq \text{ avec } \varepsilon=\pm 1$$

On en tire

$$X + Y = 3 \varepsilon \lambda q^2 , X - Y = 3 \varepsilon \lambda p^2, Z =\lambda pq$$

puis

$$X=\frac{\varepsilon \lambda}{2} (3q^2+p^2), Y=\frac{\varepsilon \lambda}{2} (3q^2-p^2), Z =\lambda pq \text{ (F)}$$

Compte tenu des hypothèses que nous avions été amenés à faire sur le signe de Y et Z, on voit que toute solution dans \(\mathbb Z\) de l’équation \(X^2 = Y^2 + 3Z^2\) est de la forme

$$X=\pm \frac{\lambda}{2} (3q^2+p^2), Y=\pm \frac{\lambda}{2} (3q^2-p^2), Z =\pm \lambda pq$$

où p, q et \(\lambda\) sont trois entiers naturels non nuls et où les signes ± sont indépendants.

Réciproquement, on vérifie immédiatement que tout triplet défini par les formules (F) ci-dessus est solution de \(X^2 = Y^2 + 3Z^2\). Encore faut-il contrôler que ces valeurs X, Y, Z sont entières.

Si \(\lambda\) est pair, le résultat est évident. Si \(\lambda\) est impair, il est nécessaire et suffisant que \(3q^2 + p^2\) et \(3q^2 - p^2\) soient pairs, ce qui est réalisé si et seulement si p et q ont même parité.

Remarque 1 : on voit aussitôt que les solutions de \(X^2 = Y^2 + 3Z^2\) dans \(\mathbb N\) sont données par

$$X=\frac{\lambda}{2} (3q^2+p^2), Y=\frac{\lambda}{2} |3q^2-p^2|, Z =\lambda pq \text{ (F)}$$

avec p, q, \(\lambda\) entiers naturels non nuls, et \(\lambda\) pair ou p et q de même parité.

Remarque 2 : la même méthode permet de traiter toute équation du type \(X^2 = Y^2 + kZ^2\), où k est premier. Elle s’applique également (avec d’ailleurs quelques simplifications) à l’équation \(X^2 = Y^2 + Z^2\) .

<redacteur|auteur=500>