Exercices

Exercice 516-1 Paul-Alain Bonvert – Alfa du Ginseng ils sont fous ces anglo-saxons !
Pour les nombres rationnels positifs l’écriture \(a \dfrac{b}{c}\) du nombre \(a + \dfrac{b}{c}\) ,dans laquelle \(a\),
\(b\) et \(c\) sont des entiers naturels avec \(b \geq c\) permet la curieuse égalité suivante :

$$\sqrt {2 \dfrac{2}{3}}= 2 \sqrt{\dfrac{2}{3}}.$$

Donner une méthode de génération d’autres exemples pour lesquels \(\sqrt {a \dfrac{b}{c}}= a \sqrt{\dfrac{b}{c}}.\)

voir l’article où est publiée une solution

Exercice 516-2 pour nos élèves

A – transmis par Vincent Thill
Peut-on trouver cinq entiers naturels consécutifs qui vérifient l’égalité

$$a^2 +b^2 +c^2 = d^2 +e^2 ? $$

B –

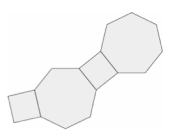
On assemble alternativement des carrés et des
heptagones réguliers comme le montre la figure
ci-contre.
Si on poursuit cet assemblage en tournant toujours de
la même façon, la boucle se fermera-t-elle
exactement ?
(si oui, combien y aura-t-il de carrés ?
d’heptagones ?)

voir l’article où est publiée une solution

Exercice 516-3 Jean-Christophe Laugier – Rochefort

1) Quel est le nombre maximal de chiffres égaux, distincts de zéro, pouvant terminer
l’écriture décimale du carré d’un entier ?
2) Montrer que l’écriture décimale d’un cube peut se terminer par un nombre
arbitraire de chiffres égaux, distincts de zéro.

voir l’article où est publiée une solution

Exercice 516-4 Izán Péraz – ?

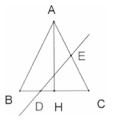
ABC est un triangle isocèle de sommet principal A tel que
AH = BC où H désigne le pied de la hauteur issue de A.
Une droite traverse le triangle en coupant la base [BC] en D et
l’un des deux autres côtés en E.
Quelle est la probabilité que DE soit supérieure ou égale à
BC ?
voir l’article où est publiée une solution

Solutions

Exercice 514-1 Marie-Nicole Gras – Le Bourg d’Oisans

On considère un triangle ABC ; on désigne par A’, B’ et C’ les milieux respectifs des
côtés [BC], [CA] et [AB].
Soient M le milieu de [A’C], N le milieu de [B’A] et P le milieu de [C’B].
Soient J le point d’intersection de [B’P] et [C’M], K le point d’intersection de [C’M]
et [A’N] et L le point d’intersection de [A’N] et [B’P].
Calculer l’aire \(s\) du triangle JKL en fonction de l’aire S du triangle ABC.

Solution de Pierre Renfer (Saint Georges d’Orques)

Autres solutions : Marie-Nicole Gras (Le Bourg
d’Oisans), Raymond Heitz (Névez), Annie Perrot (Paris), Jean-Paul Thabaret
(Grenoble), Daniel Vacaru (Pitesti), Michel Sarrouy (Mende) .

Remarque
Michel Sarrouy propose une solution basée sur un réseau de parallèles, dont la
justification relève également des barycentres.
Sa proposition est disponible sur le site de l’association.

Nota
Ayant retrouvé après envoi un exercice similaire – n° 474-3 (solution dans le BV 476) – Marie-Nicole Gras m’avait proposé de ne pas retenir celui-ci (on retrouve
effectivement la demande du 474-3 après avoir tracé le triangle A’B’C’ des milieux :
montrer que JKL occupe un septième de A ’ B ’ C ’ ). J’ai tout de même souhaité vous le
proposer.

Exercice 514-2 pour nos élèves

A – d’après le concours mathématique du Québec de 1987
Effectuer le produit suivant :

$$ \left( 1 - \dfrac{1}{2^2}\right) \left( 1 - \dfrac{1}{3^2}\right) \left( 1 - \dfrac{1}{4^2}\right) \ldots \left( 1 - \dfrac{1}{2015^2}\right).$$

B – tiré du concours canadien de mathématiques de 2011
Dans un carré magique, les nombres de chaque rangée, de chaque colonne et de
chaque diagonale ont la même somme.
Le tableau ci-dessous est un carré magique tel que les nombres \(a, b\) et \(c\) soient
strictement positifs.

$$\begin{array}{|c|c|c|} \hline \log a & \log b & \log x \\ \hline p & \log y & \log c \\ \hline \log z & q& r \\ \hline \end{array}$$

Exprimer le produit \(xyz\) en fonction de \(abc\).

Solution de Annie Perrot (Paris)

Autres solutions : Pierre Renfer (Saint Georges d’Orques), Marie-Nicole Gras (Le Bourg
d’Oisans), Raymond Heitz (Névez), L.G Vidiani (Fontaine les Dijon), Jean-Paul Thabaret (Grenoble), Daniel Vacaru (Pitesti), Françoise
Magnan (Toulouse), Michel Sarrouy (Mende).

Nota
L’énoncé B comportait la demande d’exprimer le
produit \(xyz\) en fonction de \(abc\) et non en fonction de \(a\), \(b\)
et \(c\).
Veuillez nous excuser pour cette coquille restée inaperçue.

Exercice 514-3 tiré du « livre de ce qui est nécessaire à l’artisan en constructions géométriques »

La construction décrite ci-après propose l’inscription d’un
triangle équilatéral dans un pentagone régulier.
ABCDE est un pentagone régulier, F est le milieu de [AB].
G est le centre du cercle de diamètre [FD].
Le cercle de centre F passant par G recoupe ce premier
cercle en H et I.
Les droites (DH) et (DI) recoupent le pentagone en J et K.
Le triangle DJK répond à la demande.
Cette construction est-elle exacte ?

Solution de Marie-Nicole Gras (Le Bourg
d’Oisans)

Autres solutions : Pierre Renfer (Saint Georges d’Orques), Raphael Sinteff (Nancy), Raymond Heitz (Névez), Annie Perrot (Paris),
Jean-Paul Thabaret (Grenoble), Daniel Vacaru (Pitesti), Michel Sarrouy (Mende).

Remarque
Annie Perrot précise que la construction
serait la même pour inscrire un triangle équilatéral
dans tout polygone régulier admettant un nombre
impair de côtés.

Nota
On trouvera cet exercice du mathématicien
persan Abu l-Wāfā’, pages 193 à 195 du chapitre 7
écrit par Marc Moyon dans « Les constructions mathématiques avec des instruments
et des gestes » paru chez Ellipse et dont la recension a été faite dans le BV 513.

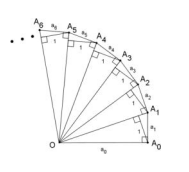
Exercice 514-4 Crux Mathematicorum
Mathematical Mayhem 114
Dans le simili escargot de Pythagore ci-contre, les
hauteurs relatives aux hypoténuses mesurent une
unité.
Les \(a_{i}\)
désignent les mesures des segments.
Montrer que

$$ a_{0}^2+a_{1}^2+a_{2}^2 + \ldots + a_{n}^2= a_{0}^2a_{1}^2 a_{2}^2 \ldots a_{n}^2$$

Solution de Pierre Renfer (Saint Georges d’Orques)

Autres solutions : Marie-Nicole Gras (Le Bourg d’Oisans), Jean-Yves Hély (Rennes).

Remarque
L’initialisation au rang 0 répond parfaitement à la demande. Toutefois
pour une adaptation en classe de cet exercice, il sera certainement préférable de faire
étudier le cas du triangle \(OA_{0} A_{1}\) . Démontrer qu’au rang 1 on a bien \(OA_{1}^2 = a_{0}^2 a_{1}^2\) met
en place le principe de l’hérédité de la seconde récurrence.

 Télécharger l’article en pdf dans son intégralité
<redacteur|auteur=500>