THÈMES : DENOMBREMENTS, SUITES

ÉNONCÉ

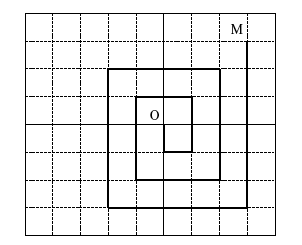
La « spirale »

Le plan muni d’un repère orthonormal d’origine O (unité 1 cm), est quadrillé
de droites parallèles aux axes de coordonnées et passant par tous les points à
coordonnées entières du plan.
Sur ce quadrillage, on construit, en partant du
point O vers le bas, une ligne brisée en forme de « spirale » qui « tourne dans le
sens contraire des aiguilles d’une montre », conformément au dessin ci-dessous.

Pour tout point M à coordonnées entières, on note \(\ell (M)\) la longueur de la portion
de « spirale » qui va du point O au point M.

1) Soit A un point de l’axe des abscisses tel que OA = 5.

Déterminer les valeurs possibles de \(\ell (A)\).

2) Soit B le point de coordonnées (2005 ; 2006).

Déterminer \(\ell (B)\).

3) Déterminer les coordonnées du point C tel que \(\ell (C) = 2006\).

4) La « spirale » passe-t-elle effectivement par tous les points à coordonnées
entières du plan ?