par une équipe [1] de lecteurs du BV

À l’origine il y eut cet article [2] de Louis Rivoallan publié dans le BV n480, où l’auteur s’enthousiasmait de la découverte d’un théorème qu’il avait faite grâce à un logiciel de géométrie :

Problème 1. Dans un plan on considère un triangle ABC et un point M quelconque non situé sur les droites (AB), (BC), (CA). Soient A’, B’, C’ les orthocentres des triangles MBC, MCA, MAB. Alors les triangles ABC et A’B’C’ ont la même aire.

Rivoallan en donnait une démonstration analytique, mais nous avons été quelques-uns à vouloir en chercher une autre, purement géométrique. Nous étions d’autant plus convaincus de la possibilité d’une telle démonstration, que le théorème, bien que peu connu, n’était pas nouveau, énoncé sous forme de problème dans les éditions successives du célèbre Traité de Géométrie de Rouché et Comberousse, du début du 20e siècle. Elle fut trouvée assez rapidement par Nicole Bopp et Michel Émery, de l’université de Strasbourg et responsables de L’ouvert (revue de la régionale APMEP d’Alsace), lesquels firent remarquer en outre que les hypothèses proposées pouvaient être simplifiées et élargies, sans référence aux orthocentres, sous la forme d’un problème purement affine :

Problème 2. Soient A, B, C, A’, B’, C’ six points du plan tels que (AB’) // (A’B), (BC’) // (B’C), (CA’) // (C’A). Montrer que les triangles ABC et A’B’C’ ont même aire.

Forte de ce résultat, l’équipe de L’ Ouvert n’en est pas restée là et a trouvé plusieurs généralisations supplémentaires, dont une généralisation à l’espace :

Soient A, B, C, A’, B’, C’ six points de l’espace tels que (AB’) // (A’B), (BC’) // (B’C), (CA’) // (C’A). Montrer que les triangles ABC et A’B’C’ sont situés dans des plans parallèles et ont même aire.

Restait un mystère : pourquoi Rouché et Comberousse particularisaient-ils l’énoncé au seul cas des orthocentres ? La nouvelle forme de l’énoncé nous fait alors penser à la réciproque du théorème de Pascal sur l’hexagone inscrit dans une conique.

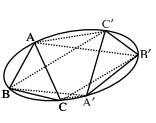
En effet, considérons l’hexagone AB’CA’BC’. Ses côtés opposés prolongés (AB’) et (A’B) ; (B’C) et (BC’) ; (CA’) et (C’A) sont concourants sur la droite de l’infini, et donc les sommets sont situés tous les six sur une conique (voir figure ci-contre). Ce qui nous rappelle aussitôt un autre théorème faisant intervenir simultanément une conique et un orthocentre : le théorème de Brianchon-Poncelet, dont voici l’énoncé :

Si un triangle est inscrit à une hyperbole équilatère alors son orthocentre est situé sur la même hyperbole.

La jonction était faite ! Le problème de Rivoallan prenait un éclairage nouveau autorisant une approche élargie en même temps que plus simple, accessible au lycée.
Ajoutons que Brianchon et Poncelet avaient publié leur théorème en 1821 dans le tome XI des Annales de Gergonne (p. 205 à 220). La lecture de leur article « Recherches sur la détermination d’une hyperbole équilatère, au moyen de quatre conditions données  » attire l’attention sur d’autres propriétés intéressantes mettant en jeu le cercle d’Euler. C’est ainsi que la rencontre entre ces trois objets : hyperbole équilatère, cercle d’Euler et orthocentre nous a incités, Marc Roux et Jean-Pierre Friedelmeyer, à rédiger l’article « Orthocentre, cercle d’Euler et hyperbole équilatère  » publié dans le numéro 487 du BV. Marc Roux y met notamment en
valeur son expérience de Geogebra et en fait une instructive activité géométrique pour le lycée.
Les choses auraient pu en rester là si Rivoallan n’avait innocemment (malicieusement ?) glissé à la fin de son article du BV 480 «  quelques conjectures à démontrer… » à propos de la même configuration de quatre points A, B, C et M, mais en considérant cette fois-ci le triangle formé par les trois centres A’, B’, C’ des cercles circonscrits aux triangles MBC, MCA, MAB respectivement, conjectures concernant la fonction $Q(M)=\frac{aire(A’B’C’)}{aire(ABC)}$
Et c’est ainsi que démarra une nouvelle aventure !

Dans un article impressionnant par son adresse calculatoire, François Duc donne une réponse analytique précise à l’ensemble des conjectures soulevées par Rivoallan et, au-delà, fait une description détaillée des lignes de niveau de Q(M), de ses variations et de ses extrema. Ces résultats mettaient en jeux des calculs sur des courbes du quatrième degré ou quartiques dont la complexité nous empêche de les présenter ici. Mais l’intérêt et la beauté des résultats nous a incités à en chercher une présentation plus géométrique, accompagnée par un fichier de géométrie dynamique qui sont le fruit du travail collectif de Marc Roux, Philippe Langlois et Jean-Pierre Friedelmeyer, et dont on trouvera le texte intégral en ligne sous le titre : Sur un problème de lieux géométriques, ainsi que le fichier Geogebra Paramétrage JPF. En voici un résumé et les résultats les plus spectaculaires.

Le problème est donc le suivant :

Étant donné dans un plan un triangle fixe ABC et un point mobile M, on désigne par A’, B’, C’ les centres des cercles circonscrits à MBC, MCA, MAB respectivement. Étudier les variations de l’aire S(M) du triangle A’B’C’ et notamment l’allure des courbes de niveau de la fonction où s mesure l’aire du triangle ABC.

Dans toute la suite, on raisonne sur les aires orientées, c’est à dire comptées positivement ou négativement selon que le triangle est ou non de sens direct. On suppose, ce qui n’est pas restrictif, que le triangle initial ABC est de sens direct. On désigne par H son orthocentre, G son cercle circonscrit, O le centre de ce cercle et R son rayon. Désignons enfin par $\Delta(P), \Delta’(P), \Delta’’(P)$ les « distances orientées » de tout point P à (BC), (CA), (AB) respectivement.

L’étude géométrique exposée en ligne nous fournit alors le résultat suivant :

$$Q(M)=\mu \Leftrightarrow (OM^2-R^2)^2+8R\mu\Delta(M)\Delta(M’)\Delta(M’’)=0$$

La courbe algébrique $L_\mu$ représentée par l’équation ci-dessus n’est pas exactement la courbe de niveau $\mu$ : elle est obtenue en lui adjoignant les points A, B, C.
Pour $\mu= 0$, on obtient le cercle $\Gamma$ compté deux fois. On écarte désormais ce cas.
C’est une quartique bicirculaire, car dans un repère orthonormal les termes de plus haut degré de son équation sont $(x^2+y^2)^2$. Elle passe par A, B et C et n’a pas d’autre point commun avec les droites (BC), (CA), (AB), ni avec le cercle $\Gamma$. Ces trois points jouent ainsi un rôle essentiel dans le tracé de la courbe.

Équation de $L_\mu$ avec origine en A :

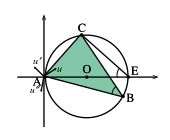
Prenons comme repère orthonormal direct $(A,\vec{i},\vec{j})$ avec $\vec{i}=\frac{\vec{AO}}{AO}$

L’équation de $\Gamma$ est donc $x^2+y^2-2Rx=0$
Appelons E le point diamétralement opposé à A sur $\Gamma$.

Supposons d’abord les angles $\widehat{B}$ et $\widehat{C}$ aigus.
Les points A, B, E, C sont dans cet ordre sur $\Gamma$.
Nous avons $\widehat{AEC}=\widehat{B}$ (relation entre angles inscrits), donc $(\vec{i},\vec{EC})=\pi-\widehat{B}$ donc le vecteur unitaire $\vec{u}’=\frac{\vec{EC}}{EC}$ a pour coordonnées $(-\cos \widehat{B},\sin \widehat{B})$

On en tire $\Delta’(M)=-x \cos \widehat{B}+y \sin \widehat{B}$
De même $\widehat{AEB}=\widehat{C}$ donc $(\vec{i},\vec{EB})=\pi+\widehat{C}$ Le vecteur unitaire $\vec{u}’’=\frac{\vec{EB}}{EB}$ a donc
pour coordonnées $(-\cos \widehat{C},-\sin \widehat{C})$. On en tire $\Delta’’(M)=-x \cos \widehat{C}-y \sin \widehat{C}$

On aboutit ainsi $\Delta’(M)\Delta’’(M)=(x \cos \widehat{B}-y \sin \widehat{B})(x \cos \widehat{C}+y \sin \widehat{C})$

Nous laissons au lecteur le soin de vérifier que la formule reste valable si l’un des deux angles ou est obtus.

En outre $\Delta(M)=x\cos\omega+y\sin\omega-l$ où $l$ est la longueur de la hauteur issue de A et $\omega$ l’angle polaire de $\vec{u}$ , vecteur unitaire normal à (BC).

L’équation de $L_\mu$ s’écrit donc

$$(x^2+y^2-2Rx)^2+8R\mu(x\cos\omega+y\sin\omega-l)(x \cos \widehat{B}-y \sin \widehat{B})(x \cos \widehat{C}+y \sin \widehat{C})=0$$

Posons R = 1 et remarquons que alors $l=b\sin \widehat{C}=2R \sin\widehat{B}\sin\widehat{C}=2 \sin\widehat{B}\sin\widehat{C}$
En coupant par une droite passant par A, avec comme paramètre sa pente t, on obtient le paramétrage suivant de $L_\mu$ , qui permet d’effectuer, à l’aide de Geogebra, les tracés
ci-après.

$$\begin{eqnarray*} x &=& \cos 2t-2\cos t \cdot K(t) \\ y&=& \sin 2t-2\sin t \cdot K(t) \end{eqnarray*}$$

Avec

$$K(t)=[ \cos(2t-\omega)-\cos\widehat{A}]\ [\mu\cos(t-\omega)\pm\sqrt{\mu^2\cos^2(t-\omega)-\mu} \ ]$$

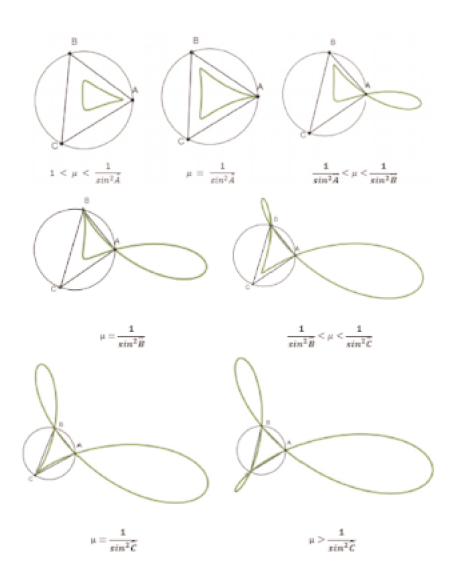
Supposons par exemple $\widehat{A}>\widehat{B} >\widehat{C}$. Quand $\mu$ augmente en partant de 1, $L_\mu$
se réduit d’abord à une courbe fermée entourant l’orthocentre H, puis, quand $\mu$ franchit la valeur $\frac{1}{\sin^2 \widehat{A}}$ , apparaît un rebroussement en A, puis une « boucle » en A, puis un rebroussement en B avec toujours la boucle en A, puis une boucle en B et en A, mais rien en C, puis …
Le nombre de cas diminue évidemment si le triangle est isocèle et a fortiori équilatéral.

Nous donnons ci-après quelques exemples de tracés dans le cas d’un triangle ayant ses trois angles aigus et inégaux.

<redacteur|auteur=500>