De nos jours, quiconque entend parler de numération binaire pense aussitôt à l’informatique. Et pourtant, depuis plusieurs siècles, les généalogistes professionnels et amateurs ont adopté un codage qui est implicitement binaire.

L’idée remonte à l’allemand Michael Eytzinger (1590) ; elle a été reprise en 1676 par Jeronimo de Sosa, franciscain espagnol, dans sa Noticia de la gran casa de los marqueses de Villafranca et popularisée par Stefan Kekule von Stradonitz dans son Ahnentafelatlas [1] (Atlas des arbres généalogiques) de 1898. L’histoire est ingrate. Oubliant Eytzinger, les généalogistes actuels parlent de numérotation de Sosa-
Stradonitz ou, plus brièvement, de numéro Sosa d’un ancêtre.

1. Le principe

1.1. Le numéro Sosa

On part d’un individu $D$, traditionnellement appelé le de cujus [2], qui reçoit le numéro 1. Puis on numérote ses ascendants selon la règle suivante : le père et la mère de l’individu numéro n reçoivent respectivement les numéros $2n$ et $2n + 1$.

Ainsi le $n^{o}4$ est le grand-père paternel de $D$, le $n^{o}5$ la grand-mère paternelle, le $n^{o}11$ la mère de celle-ci et ainsi de suite, comme dans le tableau suivant (où les chiffres entre parenthèses représentent l’écriture binaire du numéro Sosa).

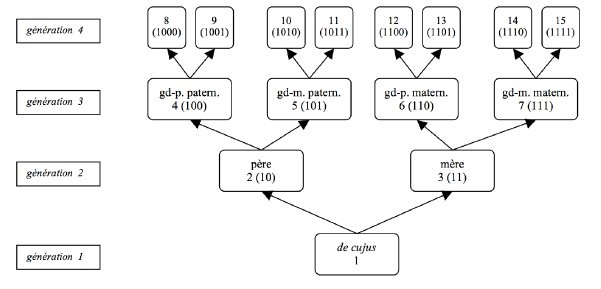
1.2. Lien entre le sexe d’un individu et son numéro Sosa

En dehors du $n^{o}1$, les numéros pairs sont masculins, les impairs sont féminins, ce qui en écriture binaire se traduit par un numéro finissant par 0 pour les hommes et par 1 pour les femmes.

Exercice 1 (facile, tiré du Rallye d’Auvergne 2003) : En utilisant uniquement les mots est, le, la, père, mère, du, de, préciser le lien entre le de cujus $D$ et son ascendant $A$ portant le $n^{o}37$.

1.3. Le numéro de génération

On numérote aussi les générations : si un individu appartient à la génération $k$, son père et sa mère appartiennent à la génération $k + 1$. Nous suivrons l’usage le plus courant, qui donne le numéro 1 à la génération du de cujus : ses parents constituent la génération 2, ses grands-parents la génération 3, etc.
À tout ascendant $A$ de $D$, on associera donc un « numéro Sosa » que nous noterons $S(A)$ et un numéro de génération $G(A)$.

1.4. Lien avec la numération binaire

On voit aussitôt que, si on écrit le numéro $n$ de $A$ en base 2, celui de son père $(2n)$ et celui de sa mère $(2n + 1)$ s’obtiennent dans la même base en ajoutant à droite de cette écriture respectivement 0 et 1.

1.5. Implexes

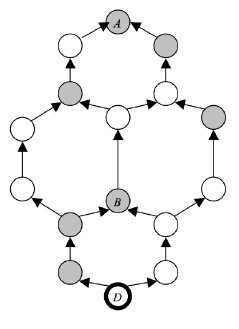
Si $D$ descend de $A$ par deux voies différentes, on dit qu’il y a implexe. $A$ (comme bien sûr tous ses ascendants) reçoit deux numéros Sosa. Si en outre ces deux voies sont de longueur différente, il reçoit aussi deux numéros de génération différents.

Exercice 2 (moyen) : Dans le schéma ci-contre, le rond le plus bas représente le de cujus $D$ ; les autres ronds sont gris pour les hommes, blancs pour les femmes ; les flèches vont du fils ou de la fille au père ou à la mère. Quelle propriété particulière possède le personnage marqué $B$ ? Quels sont les numéros Sosa du personnage marqué $A$ ?

Exercice 3 (difficile) : Sachant que la loi française autorise le mariage entre cousins germains, mais interdit [3] le mariage entre frère et sœur, entre oncle et nièce,
entre tante et neveu, supposant en outre qu’il n’y a pas de naissance hors mariage dans la famille étudiée, trouver toutes les situations où une ascendante du de cujus a deux numéros différents, inférieurs l’un et l’autre à 16.

2. Quelques questions élémentaires

2.1. Caractérisation des individus appartenant à la génération $g$

Il résulte du § 1, par une récurrence triviale, que les membres de la génération $g$ sont ceux dont le numéro Sosa comporte $g$ chiffres en écriture binaire. Ce sont donc les entiers de $[ 2^{g-1} , 2^{g}[$. Il y en a $2^{g-1}$, avec cette réserve que certains individus peuvent être comptés plusieurs fois.

Pour trouver la génération $g$ d’un individu de numéro Sosa , il suffit de compter les chiffres de son écriture binaire. Si l’on préfère, on peut observer que l’individu de numéro $s$ appartient à la génération $g$ si et seulement si $2^{g-1} \le s < 2^{g}$ ; il en résulte [4] l’égalité $ g = [log_{2}(s)]+1$.

2.2. Lignée allant de D à un ascendant A de numéro Sosa $a$

On procède dans le sens de $A$ vers $D$ : le descendant immédiat de $A$ dans le tableau porte le numéro $[a/2]$, le descendant immédiat de celui-ci le numéro $ [5].

Annexe : solution des exercices

Exercice 1 : Le $37$ est la mère du $18$, qui est le père du $9$, qui est la mère du $4$, qui est le père du $2$, qui est le père du $1$.

Exercice 2 : Le personnage B est le père à la fois du grand-père paternel et de la grand-mère maternelle de $D$, mais il les a eus de deux femmes différentes. Le personnage $A$ a six numéros Sosa différents : $138, 140, 154, 234, 236, 244.$ Il suffit pour le voir de remonter depuis $D$ en suivant le sens des flèches, de génération en
génération.

Exercice 3 : L’ascendante « double » $A$ ne peut être par deux voies différentes une grand-mère du de cujus $D$, car alors les parents de $D$ seraient frère et soeur. C’est donc au moins par une des deux voies une arrière-grand-mère, puisque ses numéros sont inférieurs à $16$.

Premier cas : $A$ est par deux voies une arrière-grand-mère de $D$. De ces deux voies, l’une passe par le père $P$ de $D$, l’autre par sa mère $M$. En effet, si par exemple les deux passaient par $P$, ce dernier descendrait de sa grand-mère par deux voies différentes ; on vient de voir que c’est impossible. $A$ est donc à la fois la grand-mère de $P$ et celle de $M$, ce qui donne les quatre schémas possibles ci-dessous :

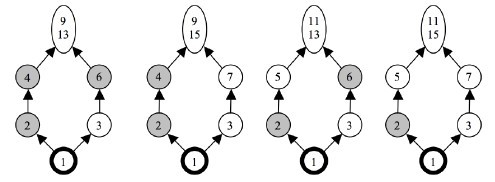
Le schéma de gauche, par exemple, se traduit ainsi : $A$ a eu deux fils $F$ et $G$ ; un fils de $F$ a épousé une fille de $G$ et de cette union de cousins germains est né $D$.

Second cas : $A$ est par une voie arrière-grand-mère de $D$ et par l’autre grand-mère de $D$. Supposons par exemple que la voie courte passe par la mère $M$ de $D$. $M$ a épousé $P$, qui est le petit-fils du père $A$ de $M$, autrement dit le fils d’un frère ou d’une
sœur de $M$. $M$ a ainsi épousé son neveu, ce qui est exclu par la loi. Ce second cas aboutit à une impossibilité.

Mais, selon l’article 164 du code civil, l’interdiction d’épouser un neveu ou une nièce peut être levée « pour des causes graves » par le Président de la République.

La configuration ci-contre est donc exceptionnelle sans être véritablement impossible. On vérifie qu’elle donne pour $A$ les
couples de numéros $(9,7)$ et $(11,7)$, la configuration obtenue en
permutant $M$ et $P$ sur le schéma donnant $(13,5)$ et $(15,5)$.

<redacteur|auteur=103>