Agnès Grimaud [1]

Construction des coefficients binomiaux en vue de l’introduction de la loi binomiale en Première S avec le nouveau programme

La réforme du programme de Première scientifique à la prochaine rentrée scolaire
m’amène à faire quelques remarques pour la mise en place de la loi binomiale.

Les coefficients binomiaux étaient connus sous la forme du triangle en Orient et au
Moyen-Orient (au X° et au XI° siècle) plusieurs siècles avant que Blaise Pascal ne
leur consacre un traité : « Traité du triangle arithmétique  » en 1654 (publié à Paris en
1665) dans lequel il donne sa construction à l’aide de la formule qui porte son nom :

$\begin{pmatrix}n \\k\end{pmatrix}$ = $\begin{pmatrix}n -1\\k\end{pmatrix}+ \begin{pmatrix}n-1\\k-1\end{pmatrix}$

et démontre 19 de ses propriétés. Avec la propriété 12, il
donne le moyen de calculer les coefficients binomiaux par la relation : $\begin{pmatrix}n \\k\end{pmatrix} = \frac {n-k+1}{k}\begin{pmatrix}n \\k-1\end{pmatrix}$
, ce qui permet de les calculer de proche en proche à partir
des $\begin{pmatrix}n \\0\end{pmatrix}$

Et il met en place pour démontrer cette propriété une première
démonstration par récurrence.

Sur un arbre représentant les répétitions d’une même expérience aléatoire, les
coefficients binomiaux comptent le nombre de chemins réalisant k succès pour n
répétitions (voir exemple ci-dessous). Il est facile pour deux, trois et quatre
répétitions de représenter l’arbre, cela devient fastidieux et très vite irréalisable au-delà
de quatre expériences de compter les chemins qui réalisent k succès parmi n
expériences identiques.

Exemple avec la répétition de 4 expériences identiques :

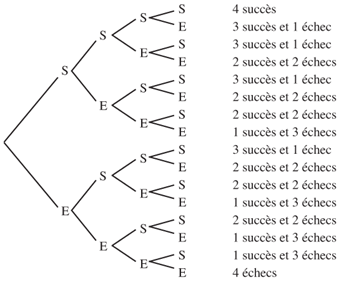
Donc il y a un seul chemin pour 4 succès donc $\begin{pmatrix}4 \\4\end{pmatrix}=1$ ;

quatre chemins pour 3 succès et 1 échec donc $\begin{pmatrix}4 \\3\end{pmatrix}=4$ ;

six chemins pour 2 succès et 2 échecs donc $\begin{pmatrix}4 \\2\end{pmatrix}=6$ ;

quatre chemins pour 1 succès et 3 échecs donc $\begin{pmatrix}4 \\1\end{pmatrix}=4$ ;

un seul chemin pour 4 échecs donc $\begin{pmatrix}4 \\0\end{pmatrix}=1$.

Pour pouvoir déterminer les coefficients binomiaux, on peut visualiser les chemins
par une ville de bord de mer, les rues étant Est-Ouest ou Nord-Sud, la plage étant
orientée NE-SO (voir schéma ci-dessous) et on compte les différents itinéraires qui
mènent à chaque point de la plage en partant d’un point donné (le sommet A du triangle) en ayant le choix entre deux directions (on peut imaginer que l’on joue à
Pile ou Face avec une pièce équilibrée avant chaque déplacement) : droite et bas (ou
ouest et sud). Pas de probas encore…

Pour trouver le nombre d’itinéraires permettant d’arriver à un point (en chaque point
on comptabilise le nombre de chemins qui y arrivent), on ajoute les valeurs des
points les plus proches de la diagonale précédente.

Par exemple : cette situation concrète nous permet de déterminer les coefficients
binomiaux dans le cas k = 4, voir schéma :

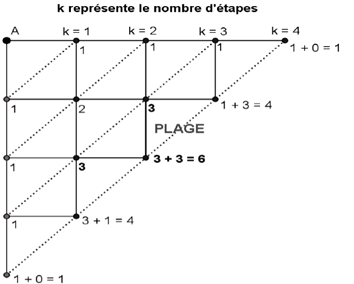
Nous avons en tout 16 chemins (c’est-à-dire $2^4 $ chemins différents), ce qui
correspond bien au nombre de branches de l’arbre de répétitions.

On peut aussi remarquer que le nombre de chemins différents pour 1, 2 ou 3
expériences correspond bien : $2^1$, ${2^2}$ ou ${2^3}$, il suffit de les comptabiliser au niveau de
la diagonale correspondante au nombre d’étapes.

De manière générale, le nombre total de chemins pour n expériences est $2^n $ (ceci se
démontre par le théorème de récurrence mais pas en Première où on se contente de
le conjecturer).

Étude des coefficients binomiaux dans le cas général

Comment déterminer les coefficients binomiaux ou à quelles règles obéissent-il dans
le cas de n expériences identiques ? Avec nos notations, dans le cas de n expériences
identiques, on atteint n + 1 points distincts de la plage en exactement n étapes en
partant du point A.

 Pour arriver aux extrémités du bord de la plage : un seul itinéraire correspond
(toujours la même direction : droite pour l’une et bas pour l’autre).

D’où, avec la notation des coefficients binomiaux, on a : $\begin{pmatrix}n\\0\end{pmatrix}=\begin{pmatrix}n \\n\end{pmatrix}=1$
 Donc par symétrie, on a : $\begin{pmatrix}n\\k\end{pmatrix}=\begin{pmatrix}n \\n-k\end{pmatrix}$
 En chaque point de la plage, pour compter les itinéraires il suffit d’ajouter les
valeurs des points les plus proches de la ligne précédente (qui correspond à n - 1
étapes).

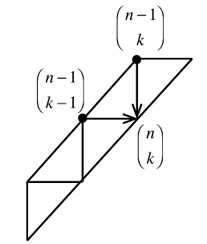
D’où, avec la notation des coefficients
binomiaux, on a la relation de Pascal : $\begin{pmatrix}n-1\\k\end{pmatrix}=\begin{pmatrix}n-1\\k-1\end{pmatrix}=\begin{pmatrix}n\\k\end{pmatrix}$

 Supposons qu’un promeneur probabiliste se rende à la plage en jouant à pile ou
face avec une pièce équilibrée. La variable aléatoire donnant le point d’arrivée du
promeneur sur la plage suit une loi binomiale de paramètre $\frac{1}{2}$ ; en effet on fait le
quotient entre le nombre d’itinéraires favorables et le nombre total d’itinéraires. La
formule dans le cas de la loi binomiale de paramètre $\frac{1}{2}$ se déduit sans problème : la
probabilité de k succès (donc n - k échecs) parmi n expériences identiques, où la
probabilité du succès est égale à la probabilité d’échec, est donnée par : $\begin{pmatrix}n\\k\end{pmatrix}\frac{1}{2^n}$

Pour arriver à ces résultats, on ne se sert jamais de l’indépendance des expériences,
on utilise seulement l’hypothèse d’équiprobabilité des itinéraires.

Pour le cas général, on procède comme indiqué dans le programme.

Remarque sur le calcul explicite des coefficients binomiaux.

Cette partie n’est pas un attendu du programme et on doit se passer de ce résultat
pour tous les calculs avec une binomiale en Première.

 En utilisant la règle 12 du Traité du triangle arithmétique de Pascal, on montre :
$\begin{pmatrix}n\\1\end{pmatrix}= \frac{n-1+1}{1}\begin{pmatrix}n\\0\end{pmatrix}=n$

Or $\begin{pmatrix}n\\1\end{pmatrix}= \begin{pmatrix}n\\n-1\end{pmatrix}$par la propriété de symétrie.

On peut aussi le montrer en comptant le nombre des itinéraires pour arriver à ce
point : pour calculer $\begin{pmatrix}n\\1\end{pmatrix}$ , il faut n directions vers le bas et 1 vers la droite donc n
itinéraires différents.
D’où, avec la notation des coefficients binomiaux, on a : $\begin{pmatrix}n\\1\end{pmatrix}=\begin{pmatrix}n\\n-1\end{pmatrix}=n$

 Toujours en utilisant la règle 12 du Traité du triangle arithmétique de Pascal, on
montre :

$\begin{pmatrix}n\\2\end{pmatrix}= \frac{n-2+1}{2}\begin{pmatrix}n\\1\end{pmatrix}=\frac{n(n-1)}{2}$

et $\begin{pmatrix}n\\3\end{pmatrix}= \frac{n-3+1}{2}\begin{pmatrix}n\\2\end{pmatrix}= n \left(\frac{n-1}{2} \right)\left(\frac{n-2}{3}\right)$

D’où, avec la notation des coefficients binomiaux, on a : $ \begin{pmatrix}n\\2\end{pmatrix}= \begin{pmatrix}n\\n-2\end{pmatrix}= \frac{n(n-1)}{2}$

et

$ \begin{pmatrix}n\\3\end{pmatrix} = \begin{pmatrix}n\\n-3\end{pmatrix}= n \left(\frac{n-1}{2} \right)\left(\frac{n-2}{3}\right)$

 D’où, la formule générale, pour n expériences et k entier, $k \in n$ qui se démontre
en utilisant le théorème de récurrence :
$ \begin{pmatrix}n\\k\end{pmatrix} = n \left(\frac{n-1}{2} \right)\left(\frac{n-2}{3}\right)x \cdots x\frac{n-(k-1)}{k}$

Extrait du nouveau programme de Première S

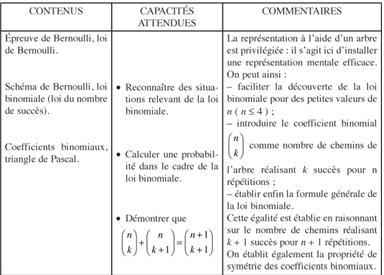
<\math>

Référence :

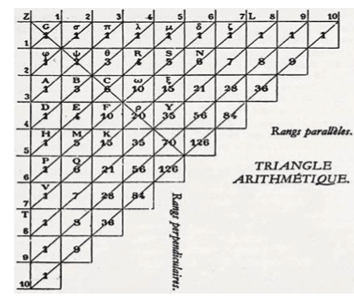
Le traité du triangle arithmétique de Pascal dont voici le début, la suite se trouve
sur Google livre.

Le résultat des travaux de recherche faits par des élèves du lycée (élèves que j’ai
eu en terminale et pour l’un aussi en première) lorsqu’ils étaient en seconde dans le
cadre du club « Math en Jeans » a été exposé par ces trois élèves devant leurs
camarades qui avaient été très intéressés. Trouver leur travail

et aussi dans : le Bulletin vert n° 482 p 371