500
Exercices deci dela du BV 500 Et solutions 498-1, 498-2 et 498-3
Exercices
Exercice 500-1. On n’a pas tous les jours 100 ans (Heu …, c’est tous les combien déjà ?)


La figure 0 correspond à une affiche de 2010. Chaque année l’APMEP se plie en quatre pour promouvoir l’enseignement des maths. Le pliage est celui qui correspond aux figures successives. Un qui n’y voit pas plus loin que le bout de son nez, dirait volontiers que l’association va y perdre son âme et donnerait la figure 9 en exemple.
Sottise [1] ! Les figures 16 et 17 montrent bien que les apparences étaient trompeuses !
Question : démontrer que, mathématiquement parlant, l’affiche du bicentenaire pourrait être la figure 10 ; c’est à-dire-que la figure 100 est identique à la figure 10 [2] .
Indication : la figure 0 et donc ses suivantes font très exactement 256 \(\times\) 256 pixels et le logiciel utilisé « ne fait que » déplacer ceux-ci de manière analogue à chaque étape.
Source et aide. Cet exercice s’inspire très largement de celui proposé comme paradoxe par Jean-Paul Delahaye en page 30 de la revue canadienne Accromath (Vol. 6 • été – automne 2011) disponible gratuitement en ligne
L’image de l’affiche a été travaillée par le logiciel créé par Philippe Mathieu, comme indiqué dans l’article de la revue, et qui est disponible, et téléchargeable gratuitement lui aussi
Je vous invite naturellement à consulter ces deux trésors !
L’image 256 \(\times\) 256 de la figure 0 est téléchargeable sur le site de l’association.
Voir l’article où est publiée la solution
Exercice 500-2. Le tore de la Tortue (d’après une activité de l’IREM de Paris Nord)
La figure ci-dessous a été tracée avec la Tortue Logo.

Si vous connaissez le langage Logo, écrire une procédure permettant d’obtenir cette figure ; sinon écrire un algorithme qui le permettrait. Dans celui-ci, à partir d’un point donné on peut tracer un trait de longueur donnée et tourner à droite (ou à gauche) d’un angle donné (en sus des règles habituelles de l’algorithmique).
C’est naturellement plus esthétique avec les couleurs, mais on peut s’en dispenser dans la construction du motif.
Source et aide. Cette activité – donnée avec un petit coup de pouce dans sa consigne originale – constitue le point d’orgue de la trentaine de celles que proposent Jean-François Jamart, Stéphan Petitjean, Erwan Adam et Salvatore Tummarello à des élèves de collège sur le site de l’IREM de Paris Nord [3]
Le logiciel GéoTortue utilisé, développé depuis 2008 par Salvatore Tummarello, y est directement téléchargeable. GéoTortue dispose également d’un site propre
Solutions
Exercice 498 - 1 Un problème de lieu (Olympiades soviétiques 1966)
On considère un triangle ABC d’un plan \(\cal{P}\) , un point M de l’espace n’appartenant pas à \(\cal{P}\) et son projeté orthogonal H sur \(\cal{P}\) .
Le point M est tel que MH est la plus petite des quatre hauteurs du tétraèdre ABCM.
Déterminer le lieu de H.
Télécharger la solution de Raymond Heitz (Piriac) en pdf
Autres solutions : Jean Gounon (Chardonnay), Bernard Collignon (Coursan).
Remarque. Bernard Collignon précise que dans le cas où H est situé sur un côté du triangle anti-complémentaire, une au moins des trois aires (ABH), (ACH) ou (BCH)est égale à (ABC) et donc une au moins des trois aires (ABM), (ACM) ou (BCM) sera supérieure à (ABC).
Exercice 498-2 (Daniel Reisz – Auxerre)
On joue 20 fois à pile ou face et on obtient :
$$00\ 11\ 0000\ 1\ 0\ 11\ 00000\ 1\ 00.$$
On regroupe les blocs formés par le même chiffre (comme suggéré typographiquement). Ici il y en a 9.
De tels blocs s’appellent des runs en anglais.
Un élève est censé avoir joué 50 fois à pile ou face et prétend avoir obtenu le résultat suivant :
$$1010110100101100010100101011000101010011001010100 ;$$
soit 36 runs.
La probabilité d’un nombre si élevé de runs est très faible et fait douter de la réalité des lancers.
Écrire un algorithme qui simule 100 lancers de 50 « pile ou face », qui compte le nombre de runs et imprime leur nombre moyen.
Solutions : Bernard Collignon (Coursan), Alain Jaeckel (Strasbourg), Baptiste Delarocque (Rouen), Olivier Reboux (Le Havre), Nicolas Patrois (?).
Leurs différents algorithmes, programmes, écrits sous Algobox, TI N’spire CAS et Python sont disponibles ici.
Supplément d’Alain Jaeckel (Stasbourg)
On observe un nombre moyen de runs proche de 25,5, soit . La curiosité l’emportant, on peut se consacrer au cas général…
Télécharger le supplément en pdf
Exercice 498-3 (Galet rond ?)
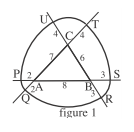
La figure 1 ci-contre est issue de l’article « L’art d’arrondir les angles » de Julien Moreau (voir à la rubrique Dans nos
classes du présent bulletin).
Prouver que les points P, Q, R, S, T et U sont cocycliques et
préciser le centre du cercle.
Télécharger la solution de Marcel Bauval (Versailles)en pdf
Autres solutions : Raymond Heitz (Piriac), Bernard Collignon (Coursan), Jean-Yves Le Cadre (Saint Avé), Michel Sarrouy (Mende), Nicolas Patrois (?).
Exercice 498-4 (Pour nos élèves) exercices tirés de La feuille à problèmes de l’IREM de Lyon
« Nos élèves » n’ont pas été très loquace…
Dans l’attente de réelles solutions d’élèves que j’aurais plaisir à faire paraître, voici les réponses sans commentaire.
- f est une fonction affine. On sait que 1,2 < f(1) < 1,4 et 3,3 < f(2) < 3,6. Que peut-on dire de f(10) ?
En 2012, on peut utiliser Geogebra pour émettre une conjecture.
Réponse : 9,95 < f(10) < 12.
- Trouver un polynôme à coefficients entiers admettant \(\sqrt 2 +\sqrt 3\) comme racine.
Réponse : \(P = x^4 - 10x^2 + 1\) est un polynôme possible.
- La suite

a-t-elle une limite ? Si oui, laquelle ? Si non, pourquoi ?
Réponse : Oui, \(\frac{\sqrt 2}{2}\)
<redacteur|auteur=500>































