Marc Girault [1]

Le Bulletin de l’APMEP a déjà abordé ce thème, notamment à travers l’article de Dany-
Jack Mercier, Cryptographie classique et cryptographie publique à clé révélée, septembre
1996.

1. Introduction

- 1.1. Définition

Si l’on en croit Jacques Stern [2], la cryptologie (ou cryptographie) est la « science du
secret », aujourd’hui étendue à la « science de la confiance ». Ses missions
principales sont de définir des méthodes, appelées improprement « algorithmes » (ou
encore « mécanismes », « schémas », « systèmes », etc.) permettant d’assurer la
confidentialité, l’intégrité et l’origine des données, ainsi que d’en évaluer la sécurité.
Pour cette dernière tâche, le savoir-faire des cryptanalystes, qui recherchent les
failles des algorithmes proposés, est particulièrement apprécié. Afin de diminuer les
chances de tomber sous leurs fourches caudines, les cryptographes (qui sont plus ou
moins les mêmes personnes, ce n’est qu’une question de casquette !) ne spécifient
plus que des algorithmes dotés de preuves, au moins partielles, de sécurité.

- 1.2. Un mot d’histoire

L’histoire de la cryptographie est pluri-millénaire
 [3] , et il ne s’agit pas ici de la
retracer. Indiquons simplement qu’on peut facilement distinguer deux périodes :
 la période artisanale, très longue, qui démarre à la nuit des temps (bien avant les
hiéroglyphes !) pour expirer en même temps que la domination qu’Hitler entendait
exercer sur le monde, et au service de laquelle la fameuse machine à rotors Enigma,
visible au Mémorial de Caen, devait jouer un rôle-clé. Mais Alan Turing et ses
équipes du Bletchley Park, dotés des premiers ordinateurs, aidés des découvertes
polonaises et françaises, mirent tous leurs talents à en percer les secrets, et
contribuèrent ainsi à déjouer les plans du dictateur fou ;
 la période scientifique, encore très courte puisqu’elle débute en 1949, date où
Shannon commença à mettre de l’ordre dans la discipline en même temps qu’il fonda
la théorie de l’information [4]. Les autres dates marquantes de cette période furent,dans un incroyable tir groupé de trois ans : 1974 (invention du DES [5] ou Data
Encryption Standard), 1976 (invention de la cryptographie à clé publique [6]) et 1977
(invention de RSA [7], pour Rivest, Shamir et Adleman, et accession du DES au titre
de norme fédérale américaine). Mentionnons également 1985 (invention du zeroknowledge [8]) et 1998 (invention de l’AES [9]., Advanced Encryption Standard, norme
fédérale américaine depuis 2000).

Une autre date importante, mais d’intérêt essentiellement hexagonal, est 1999. On y
assista au basculement complet du statut de la cryptologie qui, avant cette date,
relevait des matériels de guerre de seconde catégorie (telle un … porte-avions), puis,
sans transition, fut ensuite enseignée dans les lycées [10] !

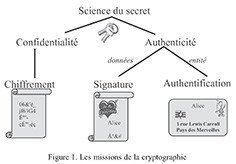
- 1.3. Les missions de la cryptographie (cf. figure 1)

Le but de la cryptographie est de fournir des moyens de lutter contre les attaques
passives, consistant à prendre frauduleusement connaissance de données transmises
ou stockées, et contre les attaques actives, consistant à modifier frauduleusement leur
origine ou leur contenu.

Pour lutter contre les attaques passives, et ce faisant assurer la confidentialité des
données, on utilise un mécanisme de chiffrement : l’émetteur chiffre les données en
clair avec une clé de chiffrement, le récepteur déchiffre les données chiffrées avec
une clé de déchiffrement. La clé de déchiffrement est nécessairement secrète, faute
de quoi tout le monde pourrait rétablir la clarté.

Pour la lutte contre les attaques actives, et ce faisant assurer l’authenticité des
données ou des entités, on distingue deux cas.

L’origine des données ainsi que leur intégrité sont assurées par une signature
numérique, produite avec une clé de signature, vérifiée avec une clé de vérification,
et dont la valeur dépend tout à la fois de celui qui signe et de ce qui est signé. Ce
dernier point la distingue d’une signature traditionnelle : un seul bit s’inverse et tout
est chamboulé ! Sur le reste, l’analogie est grande : une signature est réputée
inimitable, sa taille est réduite et indépendante de la taille des données. Quant à la clé
de signature, elle est nécessairement secrète, faute de quoi tout le monde pourrait
signer à la place de tout le monde. Le mécanisme de signature est essentiellement off-line
 : une signature peut être calculée un jour et vérifiée le lendemain ou le mois
suivant.

L’identité de l’entité (être humain, ordinateur, carte à puce, …) avec laquelle on
communique à l’instant présent est assurée par un mécanisme d’authentification,
dont le célèbre login, password constitue l’exemple le plus populaire, à défaut
d’être le plus sûr. Le mécanisme d’authentification est essentiellement on-line : il met
en présence les deux entités concernées, et son verdict (OK ou NOK) ne vaut qu’à
l’instant où il est prononcé, et éventuellement encore quelques instants après, la
définition de l’instant variant notablement avec les situations. Signature et
authentification peuvent être combinées pour assurer l’origine et l’intégrité de
données à l’instant présent.

 

2. Cryptographie versus codage

Les scientifiques utilisent le mot « codage » à toutes les sauces. Dès que l’on modifie
la façon dont une donnée est représentée, elle est déclarée « codée ». La modification
peut être plus ou moins lourde selon que l’on change le support de représentation lui-même
(par exemple la conversion analogique – numérique) ou seulement la
représentation sur un support donné (par exemple la compression de données).

Afin d’éclaircir un peu le paysage, nous allons comparer entre elles trois formes de
codage : le codage de source, le codage de canal et le codage « secret ». Ce sont dans
les trois cas des codages de deuxième type : on ne fait que modifier les mots, mais
pas l’alphabet dans lequel ils s’écrivent, en l’occurrence l’alphabet binaire 0, 1. En
d’autres termes, ces codages remplacent des chaînes de bits par d’autres chaînes de
bits, plus appropriées.

- 2.1. Codage de source

La question est ici : comment adapter la source d’information au (débit du) canal qui
la transporte ? Considérons le cas d’un disque compact (CD) dont on souhaite
transmettre le contenu à un ami par Internet (c’est interdit mais sera empêché par un
autre type de codage, voir plus loin). On y renoncera car le nombre de bits d’un CD
est trop grand, ou, si l’on préfère, le débit offert par l’ADSL est insuffisant. Il faut
trouver une représentation plus compacte (?) de cette musique, sans trop en dégrader
la qualité. En d’autres termes, il faut la comprimer. Le format MP3 est bien connu.
Les formats MPEG et DivX pour les images le sont aussi.

Les mathématiques utilisées en compression de données sont assez variées, mais
empruntent beaucoup à l’analyse et à l’intégration (dont la théorie du signal est issue)
et au calcul de probabilités (dont la théorie de l’information est issue).

- 2.2. Codage de canal

La question est cette fois : comment lutter contre les erreurs ? Reprenons notre CD
de tout à l’heure. D’abord il peut avoir été abîmé et des bits inopportunément
retournés. Le plus souvent, toute une séquence a été effacée (« 010010111110010 »
remplacée par « 000000000000000 »). Ensuite, son contenu peut avoir été altéré lors
de la transmission Internet : les canaux de communication sont loin d’être parfaits.
Le rendu final pourrait retourner Mozart dans sa tombe. La solution est d’ajouter à
l’information utile une information dite redondante, qui n’ajoute aucune note aux
Noces de Figaro (certains trouvent déjà qu’il y en a trop), mais qui permet de
détecter, et parfois même de corriger, celles qui ont été involontairement altérées. Les
procédés qui construisent cette information redondante sont appelés codes
détecteurs/correcteurs d’erreurs. L’opération qui restitue l’information initiale est
appelée décodage.

Ici, c’est l’algèbre qui est reine. Les codeurs correcteurs d’erreurs sont de fins
algébristes, incollables sur les espaces vectoriels et les corps finis. Mais ils ont aussi
besoin de bien savoir compter, ce qui implique une compétence en combinatoire.
Enfin, ils doivent avoir de bonnes notions en théorie de la complexité, cette discipline
qui classifie les problèmes mathématiques selon leur difficulté inhérente, afin de
trouver des algorithmes de décodage efficaces, ce qu’ils ne sont jamais s’ils sont pris
au hasard !

- 2.3 Codage « secret »

La question est enfin : comment lutter contre les fraudes ? Nous retrouvons notre CD
de Mozart dont les droits d’auteurs (détenus par les interprètes) s’accommodent mal
de sa diffusion gratuite et impunie sur Internet. Une solution serait de chiffrer l’opéra
avant de le graver, le mélomane qui l’écoute ou l’internaute qui le télécharge ne se
voyant donner la clé de déchiffrement que s’il s’est acquitté des droits
correspondants. Cette fois-ci, c’est la cryptographie que l’on appelle à la rescousse.

La cryptographie est un bonheur pour une partie des arithméticiens, car elle est le
seul domaine d’application connu de la théorie des nombres. Pour les autres, c’est un
cauchemar, pour exactement la même raison (selon eux, une belle théorie ne doit pas
avoir d’applications). Mais le cryptographe devra aussi goûter l’algèbre, si possible
même la géométrie algébrique (notamment les courbes elliptiques), ainsi que,
comme pour le codeur de canal, les probabilités et la théorie de la complexité.

3. Les deux fois deux (= trois !) cryptographies

Il existe deux cryptographies, mais comme il y a (au moins) deux façons de dessiner
la frontière, cela en fait un peu plus en tout.

Première façon : la cryptographie peut être inconditionnelle ou calculatoire.
Deuxième façon : la cryptographie peut être symétrique ou asymétrique.

Précisons tout de suite que la cryptographie asymétrique est nécessairement
calculatoire. Cette remarque inspire l’exercice suivant :
 1) Compléter les points dans la phrase : « Donc la cryptographie … ne peut être
que … » différemment de ci-dessus.
 2) En déduire le nombre total de cryptographies différentes (indice : relire le titre
du paragraphe).

- 3.1. Les cryptographies inconditionnelle et calculatoire
La cryptographie inconditionnelle ne repose que sur le secret du … secret. Elle ne
pré-suppose pas que tel ou tel problème mathématique serait hors de portée d’un ou
plusieurs êtres humains muni(s) d’un ou plusieurs ordinateurs. Avec elle, les choses
sont claires. Les théorèmes qu’elle produit sont de la forme : « Si le secret a été bien
gardé, alors : ou bien la probabilité de réussite d’un ennemi est inférieure à $\epsilon$ = [compléter], ou bien l’ennemi est un extra-terrestre ».

La technique du code confidentiel pour les cartes bancaires relève de cette
cryptographie. Le théorème s’énonce dans ce cas de la façon suivante : « Si le code
confidentiel n’est pas écrit au revers de la carte et si le client s’entoure d’un rideau
de protection avant de le saisir sur un distributeur de billets de banque, alors : ou bien
la probabilité d’un voleur de carte est inférieure ou égale à $\epsilon$ = 0,003 (car il a droit à
trois essais avant que la carte ne se bloque), ou bien le voleur de carte a des dons de
voyance ».

Par contraste, la cryptographie calculatoire repose de surcroît sur un acte de foi. Cet
acte de foi s’énonce ainsi : « Il existe des fonctions à sens unique ». Une fonction à
sens unique est facile à calculer (au moins avec un ordinateur), mais pratiquement
impossible (même avec mille ordinateurs) à inverser (par « inverser » on entend ici :
« trouver un antécédent, s’il existe »). Cependant, cette impossibilité n’est pas
absolue : un ennemi doté d’une puissance de calcul phénoménale (introuvable sur
terre, par exemple infinie !), trouverait l’antécédent recherché. Cela n’a pas
d’importance, tant que nous restons sur notre bonne vieille planète.

Le souci est que cette impossibilité relative n’est pas assurée : on n’est jamais à l’abri
de la découverte d’une méthode d’inversion révolutionnaire. Les théorèmes que cette
cryptographie produit sont de la forme : « Si le secret a été bien gardé, alors : ou bien
la probabilité de réussite d’un ennemi est inférieure à environ $\epsilon$ = [compléter], ou
bien l’ennemi est un mathématicien génial, ou encore l’ennemi est un extraterrestre
 ».
En d’autres termes, la cryptographie calculatoire n’est possible que parce
que les mathématiciens vivant sur terre sont incompétents (en souhaitant qu’ils le
restent).

Il y a pire : non seulement on ne connaît pas de fonction qui soit à sens unique de
façon démontrée, mais on ne sait même pas démontrer qu’il en existe. Et pour finir
d’enfoncer le clou, on a peu d’espoir de le démontrer un jour, puisque tomberait du
même coup la conjecture la plus notoire de la théorie de la complexité (à savoir :
$P \neq­ NP$, l’équivalent dans cette discipline du grand théorème de Fermat en
mathématiques ou plutôt, puisque ce dernier a fini par céder un peu avant que nous
changions de millénaire, l’hypothèse de Riemann).

Malgré toutes ces mauvaises nouvelles, c’est pourtant la cryptographie calculatoire
qui sécurise nos paiements, protège nos conversations téléphoniques et empêche les
non-abonnés de regarder Canal+ (ou si elle ne les empêche pas, c’est pour d’autres
raisons). La raison en est simple : c’est la seule qui soit vraiment pratique. Nous
verrons, en étudiant de près son exemple-phare, que la cryptographie
inconditionnelle est trop luxueuse ou trop contraignante pour espérer rencontrer un
jour le succès.

- 3.2. Les cryptographies symétrique et asymétrique

Pour fabriquer des fonctions à sens unique, il existe deux approches. Étonnamment,
elles ne concernent pas du tout les mêmes mathématiciens, même si certains sont
suffisamment brillants pour pratiquer les deux avec succès.

Symétrique
La première approche consiste à faire « n’importe quoi », mais pas « n’importe
comment ». On espère ainsi que la voie de retour soit suffisamment inextricable pour
ne jamais aboutir. Faire « n’importe quoi », c’est torturer des chaînes de bits d’entrée
dans tous les sens de façon qu’il n’en reste qu’une bouillie indigeste, dont les
ingrédients de départ ne soient pas identifiables. Torturer des chaînes de bits, c’est les
mélanger entre elles

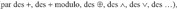
c’est en
permuter le contenu (le bit de position 7 se retrouve en position 51), c’est remplacer
des petits blocs par d’autres petits blocs (en consultant une table de correspondance),
etc., etc., le tout en conservant un contrôle fin de ce que l’on fait car, comme l’a
brillamment démontré Knuth [11] au début du volume 2 de sa collection de légende,
lorsque l’on fait n’importe quoi n’importe comment, on ne fait finalement pas
n’importe quoi.

Cette façon de procéder est réservée à des mathématiciens très intuitifs, capables de
repérer un chêne dans un forêt de hêtres, et très rigoureux, car ils doivent à leur tour
éviter de laisser traîner un seul chêne derrière eux. Techniquement, ils doivent être
habiles dans le calcul de probabilités. Ce sont eux à qui l’on doit des algorithmes de
chiffrement tels que le DES ou l’AES. Ce sont les petites mains de la cryptographie
symétrique.

La cryptographie symétrique a exercé un monopole absolu jusqu’aux années 70. Son
principe est conforme à l’intuition : les deux extrémités d’une communication
sécurisée partagent un même secret. Dans le cas où l’on cherche à assurer la
confidentialité des données, ce secret partagé jouera à la fois le rôle de clé de
chiffrement et de déchiffrement. L’algorithme de chiffrement prendra donc en
entrées le message en clair et la clé de chiffrement, et fournira en sortie le message
chiffré. L’algorithme de déchiffrement prendra en entrées le message chiffré et la clé
de chiffrement, et fournira en sortie le message en clair. Mais où se trouvent les
fonctions à sens unique dans tout ça ?

Quand la clé est connue, l’algorithme de chiffrement est une fonction (d’entrée le
message clair, de sortie le message chiffré) qui ne doit pas être à sens unique, car
alors le destinataire soi-même ne saurait pas déchiffrer. Ce n’est pas le but !

En revanche, quand le message clair est connu, l’algorithme de chiffrement devient
une fonction (d’entrée la clé, de sortie le message chiffré) qui doit être à sens unique,
de sorte que l’espion qui a espionné le message chiffré et capturé ou deviné tout ou
partie du message clair (peu importe comment) ne puisse pas remonter à la clé. C’est
le but !

Asymétrique
La deuxième approche pour obtenir des fonctions à sens unique est de repérer des
fonctions non faites sur mesure, qui soient « naturellement » revêches à l’inversion.
Jusqu’à un passé assez récent, c’était la chasse gardée des théoriciens des nombres et
de leurs amis, qui ont très vite déniché deux ou trois fonctions particulièrement
prometteuses de ce point de vue.

On pourrait craindre qu’il faille un Bac + 8 pour en comprendre les énoncés, mais
rien n’est plus faux. Le Bac + 8 n’est requis que pour comprendre pourquoi
l’inversion est hors de portée de la technique d’aujourd’hui, pas pour comprendre la
fonction elle-même. Je n’en veux pour preuve que la première d’entre elles qui n’est
autre que la … multiplication d’entiers ! Pour multiplier deux nombres de taille N
chiffres (ou bits), même grande, c’est facile. La méthode apprise en classe prend un
temps proportionnel au carré de cette taille (les algorithmiciens disent qu’elle est en
$O(N^2)$). Il en existe même d’autres sensiblement plus rapides, au moins
asymptotiquement, telles que celle reposant sur la Transformée de Fourier Discrète.
En revanche, de façon assez étonnante, le meilleur algorithme connu pour factoriser
des entiers reste inefficace. Il est « subexponentiel » (précisément : en
$O(exp[cN^{1/3}(log N)^{2/3}]$), où c est une constante proche de 1, et échoue nettement à
factoriser des entiers d’un millier de bits constitués en multipliant deux nombres
premiers de grandeurs comparables. Une telle taille pourrait sembler déjà élevée,
mais elle laisse en réalité beaucoup de place pour pratiquer une cryptographie qui
aurait besoin de nombres « impossibles » à factoriser, comme dans le système RSA.

Il se trouve que de telles fonctions à sens unique permettent, directement ou
indirectement, de spécifier des algorithmes sans clé secrète partagée. C’est
incroyable mais c’est ainsi. Au lieu d’une clé par paire d’entités, il y a une paire de
clés par entité. Par exemple pour le chiffrement, c’est le destinataire Bob qui devra posséder une telle paire. Elle sera constituée d’une clé privée (= secrète) pour
déchiffrer et d’une clé … publique, envoyée à l’émettrice Alice, pour chiffrer.

L’algorithme de chiffrement aura donc en entrées le message en clair et la clé
(publique) de chiffrement, et fournira en sortie le message chiffré.

L’algorithme de
déchiffrement aura en entrées le message chiffré et la clé (privée) de déchiffrement,
et fournira en sortie le message en clair. Pour retrouver la clé privée à partir de la clé
publique, il faudrait remonter le cours d’une fonction à sens unique. C’est
théoriquement possible, mais pratiquement infaisable.

4. La cryptographie au lycée

Comme indiqué ci-dessus, la cryptographie ne fait pas systématiquement appel à des
mathématiques haut de gamme. Deux des systèmes les plus célèbres, le chiffrement
une fois et RSA, ne nécessitent pour être compris qu’un bagage de lycée. Certes, il
faut tout de même être en Terminale S option mathématiques, classe dans laquelle
l’arithmétique est récemment réapparue. Ce retour avait été réclamé à corps et à cri
par les professeurs de l’enseignement supérieur, et notamment ceux de …
cryptographie !

- 4.1. Chiffrement une fois

Le chiffrement une fois (one-time pad) est une véritable curiosité mathématique. Sa
description est si simple qu’on pourrait l’enseigner en école primaire. Sa sécurité est
si totale que seul un devin pourrait la compromettre. Et la preuve si accessible qu’un
lycéen (motivé) pourrait facilement la comprendre. Hélas, sa mise en œuvre est si
compliquée que presque personne ne pourrait l’utiliser ! En effet, dans ce système, la
clé est … aussi longue que le message lui-même (et doit être renouvelée à chaque
nouveau message).

C’est à Vernam et deux autres ingénieurs du début du siècle dernier que l’on doit
cette fameuse trouvaille. Mais elle n’est pas tombée tout cru de leur chapeau. Ils ne
firent que magnifiquement parachever une évolution de vingt siècles initiée par …
Jules César soi-même !

C’est en effet au génial chef militaire que l’on doit le système qui porte son nom, et
qui consiste à remplacer la lettre A par la lettre D, B par E, etc., X par A, Y par B et
Z par C (les écoliers ont souvent recours à la version simplifiée dans laquelle chaque
lettre est remplacée par la suivante dans l’alphabet, et Z est remplacé par A).
En
faisant A = 0, B = 1, …, Z = 25, le système de César se définirait en écriture moderne
par : c = m + k (mod 26), où m, c et k sont des variables représentant des valeurs
comprises entre 0 et 25. Avec César, k est toujours égal à 3. Il n’est pas très difficile
de percer ce code de nos jours, mais on peut imaginer la perplexité de nos ancêtres
les gaulois lorsqu’ils interceptaient des messages du genre [12] :
IDLWHVWDLUHGHILQLWLYHPHQWOHVLUUHGXFWLEOHVJDXORLV
Il faudra attendre quinze siècles pour que Vigenère et d’autres l’améliorent, et trois
siècles encore pour que cette amélioration soit cassée à son tour. Dans le système dit de Vigenère, la valeur de k n’est pas la même pour chaque lettre. La clé K est
constitué d’une succession (finie) de n valeurs de k comprises entre 0 et 25. Par
exemple, si K = (6, 21, 13, 19), alors la première lettre chiffrée obéira à l’équation :
c = m + 6 (mod 26), la seconde à l’équation : c = m + 21 (mod 26), etc., et de nouveau
la cinquième à l’équation : c = m + 6 (mod 26), etc.

C’est la répétition de la clé en cycles successifs qui permettra néanmoins les
cryptanalyses astucieuses du XIXème siècle. Pour y échapper, Vernam et ses
collègues décident « simplement » (outre de travailler avec l’alphabet binaire 0, 1,
car leur invention était destinée au télégraphe), de prendre : $n =\infty$ ; excusez du
peu ! La longueur de la clé K devenant (potentiellement) infinie, la talon d’Achille
provenant de sa répétition disparaît, et avec lui l’imperfection du système de
Vigenère.

Restait à évaluer la qualité de l’algorithme de chiffrement ainsi obtenu. Ce sera la
tâche de Shannon, qui en démontrera en 1949 la sécurité parfaite et inconditionnelle,
preuve qui constitue précisément l’objet de l’exercice ci-dessous.

- 4.2. Exercice

Soit n un entier, $M = (m_1,m_2,\ldots,m_n)$ un message (en) clair, $K = (k_1, k_2,\ldots, k_n)$ une clé
de chiffrement et $C = (c_1, c_2,\ldots, c_n)$ un message chiffré par le système de Vernam,
c’est-à-dire selon l’équation :

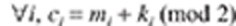
Question préliminaire : quelle est l’équation de déchiffrement ? (c’est-à-dire :
comment retrouve-t-on le message clair à partir du message chiffré et de la clé de
chiffrement ?)

Afin de démontrer la sécurité de cet algorithme de chiffrement, on assimile l’espace
des messages en clair, l’espace des clés et l’espace des messages chiffrés à trois
espaces probabilisés :

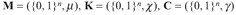
où :
 $\mu $ est une distribution de probabilité quelconque (dite « connaissance a priori » de
l’ennemi sur le message clair) ;
 $\chi$ est la distribution uniforme (chacune des $2^n$ valeurs possibles de clé est
équiprobable)
 $\gamma$ est la distribution-image de .....