Thérèse Éveilleau [1] & Richard Choulet [2]

0. Introduction

Lors d’une conférence où elle présentait son site, Thérèse Éveilleau [3] a sorti de sa besace un graphique à multiplier les entiers qui est aussi un crible pour détecter les nombres premiers. Celui-ci est dû au mathématicien Youri Matiiasevitch [2] qui utilisa une parabole. Nous proposons de découvrir ou redécouvrir cette sympathique propriété de la parabole et expliquer le caractère magique et pour tout dire unique de celle-ci dans le cadre de notre étude.

Cet article à deux mains droites est décomposé ainsi : dans la première partie Thérèse Éveilleau, dévoile deux éléments « magiques » de son site et en particulier celui lié à la parabole qui va être repris dans une seconde partie par le second auteur.

I. « Les machines graphiques »

Au cours de mes visites dans les classes, j’ai pu constater que beaucoup d’élèves de CP, CE avaient des difficultés pour manipuler un tableau à double entrée. Cela passe d’ailleurs souvent inaperçu…

Il s’ensuit, pour certains, une incapacité à comprendre et à apprendre une table d’addition et une table de multiplication.

La table suivante est très simple d’utilisation et ne demande pas de compétence particulière. Pour obtenir la somme de deux nombres, il suffit de tracer le segment joignant les deux nombres dont on cherche la somme. La somme se lit directement à l’intersection de la ligne médiane et du segment bleu.

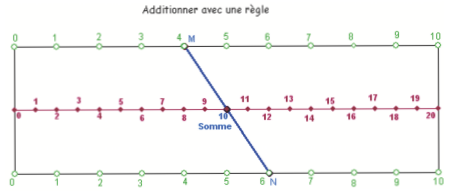
Bien entendu l’usage de cet outil ne doit pas être définitif. Cependant sa manipulation met l’accent sur la commutativité de l’addition et fait mémoriser les résultats. Cette réglette est particulièrement appréciée des enfants en difficulté scolaire et de nombreux parents m’ont écrit témoignant de leur plaisir devant la facilité d’utilisation de cet outil méconnu :
http://therese.eveilleau.pagesperso-orange.fr/pages/truc_mat/textes/addition.htm

Non bloqués momentanément par les difficultés techniques, les élèves peuvent se concentrer sur le sens de l’opération.
Le principe repose sur le théorème suivant : « L’abscisse du milieu d’un segment est égale à la demi somme des abscisses de ses extrémités ».
Aussi mon problème était-il d’imaginer le même genre d’outil pour la table de multiplication.
Je me suis alors souvenue d’une jolie propriété de la parabole [voir II. 1.].
En « couchant » la parabole [4] , on retrouve le produit de deux nombres. On peut expérimenter cet outil dans ma page :
http://therese.eveilleau.pagesperso-orange.fr/pages/truc_mat/textes/tabl_mult_russe.htm

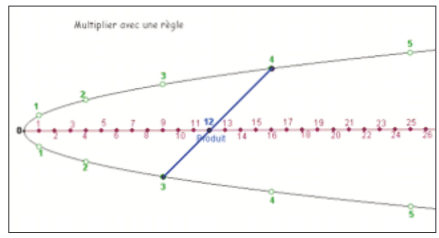
Il suffit de tracer un segment (ou simplement de placer une règle transparente), entre les deux nombres à multiplier. Le produit se lit à l’intersection de la ligne médiane rouge et de la règle bleue.

La manipulation est facile et à portée de tous les enfants en difficulté. Et ils apprécient ! Là aussi la commutativité de la multiplication est mise en valeur :
$3 \times 4 = 4 \times 3$. Les deux segments correspondant aux couples (3 ; 4) et (4 ; 3), coupent
la ligne rouge au même point d’abscisse 12.

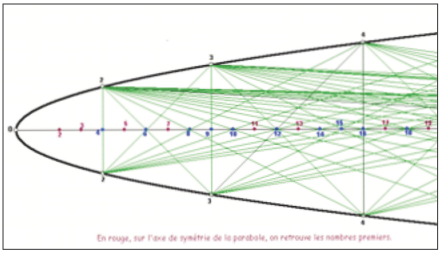
Cette propriété est utilisée également pour retrouver les nombres premiers : sur le graphique ci-dessous, les nombres notés en bleu sont le produit de nombres entiers et ne sont donc pas premiers. Les autres notés en rouge sont des nombres premiers.
C’est le crible de Matiiassevitch que l’on peut animer ici :
http://therese.eveilleau.pagesperso-orange.fr/pages/truc_mat/textes/crible_russe.htm

II. Explications sur la machine graphique qui multiplie et extension

1. Démonstration.

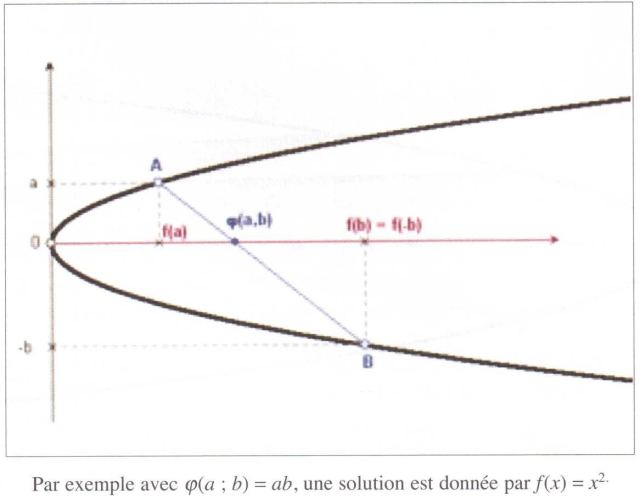
Je refais brièvement la démonstration du résultat annoncé au I., par lequel le produit est lu sur l’axe de symétrie de la parabole d’équation $y = x^2$ .
Avec les points $A(-a ; a^2)$ et $B(b ; b^2 )$, la droite (AB) a pour équation

$$y - a^2 = (b - a)(x + a),$$

après simplification par $a + b \ne 0 $
On en déduit les coordonnées du point d’intersection de (AB) avec l’axe des ordonnées : le point de coordonnées $(0 ; ab)$.

2. Généralisation.

Pour étendre le procédé précédent, qui a donc permis de lire sur l’axe des abscisses le composé de deux réels (en fait entiers ici) par une loi interne et associative, il est tentant de généraliser ainsi.

Pour se placer dans les conditions du graphique présenté dans le site (axe horizontal pour la parabole), et vu plus haut, c’est la parabole d’équation $y=\pm \sqrt x$ qui a servi.

Une généralisation possible passe par la recherche, dans un repère orthogonal, d’une courbe d’équation $y=\pm f^{-1}(x)$ de sorte que la droite (AB) avec $A(f(a) ; a$) et $B(f(b) ; -b)$ coupe l’axe des abscisses en un point dont l’abscisse soit $\varphi (a,b)$ donné, où $\varphi$ est symétrique. On pourra noter $a*b$ si l’on pense à une loi de composition interne.

En formant une équation de la droite (AB), on trouve l’abscisse [5] cherchée qui est

$$\frac{af(b)+bf(a)}{a+b}$$

L’équation fonctionnelle qui lie généralement $\varphi$ et f est donc :

$$(a + b)\varphi(a ;b)=af(b)+bf(a)$$

3. Quelques rudiments à propos de l’équation fonctionnelle $(a + b)\varphi(a ;b)=af(b)+bf(a)$

On souhaite $\varphi$ à valeurs entières pour a et b entiers, ce qui impose à a+b de diviser bf(a) + af(b).

3.1. Recherche d’une condition nécessaire lorsque $\varphi(a ;b)=ab$
Avec a = b on trouve$ f(a) = a^2$ , donc on n’a pas le choix.

3.2. La condition est-elle suffisante ?
Oui, comme on s’en assure aisément : il n’y a donc qu’une seule solution.

3.3. Quelles sont les $\varphi$ atteignables par une fonction monôme ?
$f(x) = x^3$ donne $\varphi(a ;b)=ab \frac{a^2+b^2}{a+b}$ qui en général n’est pas entier, voire jamais $(a \ne b)$, mais c’est à voir [6] !

$f(x) = x^4$ donne $\varphi(a ;b)=ab(a^2-ab+b^2)$ qui peut être envisagé !

Le seul cas finalement où on trouve f monôme et
$\varph$ cohérents est $f(x) =x^{2p}$ pour laquelle $\varphi(a ;b)=ab \frac{a^{2p-1}+b^{2p-1}}{a+b}$ qui est entier avec a et b entiers.

3.4. De manière générale et de toutes façons, une condition nécessaire est $f(x)=\varphi(x ;x)
Cette condition est suffisante lorsque :

$$(a + b)\varphi(a ; b) =a \varphi(b ; b) +b \varphi(a ; a).$$

Voilà du grain à moudre pour les meuniers qui ne dorment pas.

III. Références

[1] http://therese.eveilleau.pagesperso-orange.fr
[2] http://logic.pdmi.ras.ru/~yumat/int_vita.ht

<redacteur|auteur=500>