Le site « Images des Maths » est plein de ressources pour les professeurs du
secondaire. Encore faut-il avoir le temps de lire, de trier, de mettre en forme. Et le
temps est ce qui manque le plus ! Mais quand on est à la retraite, on a le temps de
fureter, et voici une de mes découvertes.

La substance de ce texte est l’article de Niels Berglund « La probabilité d’extinction
d’une espèce menacée », paru sur le site « Image des maths » en février 2013. Le
problème initial m’a paru à la fois très intéressant et tout à fait à la portée d’un élève
de Terminale S, mêlant avec bonheur analyse et calcul de probabilités. Je l’ai donc
cuisiné sous forme d’un énoncé de devoir à l’usage des élèves de Terminale S, très
classique dans sa forme : mon idée était de fournir un énoncé de « devoir-maison »,
et les élèves doivent alors être suffisamment guidés pour pouvoir se débrouiller tout
seuls.

On trouvera l’article initial , classé « piste noire », à l’adresse :

http://images.math.cnrs.fr/La-probabilite-d-extinction-d-une.html

On verra que je n’ai fait que modifier sa forme pour en faire un usage scolaire, sans
craindre le « copier-coller ». La fin de l’article de Niels Berglund élargit ensuite le
problème à des questions plus difficiles.

I. L’énoncé

Les modèles d’évolution de populations ont une longue histoire. Ici, il sera question
d’un modèle probabiliste, introduit en 1874 par Francis Galton et Henry William
Watson.

Supposons, pour étudier un modèle simplifié, que chaque individu a au cours de sa vie :

• aucun enfant avec une probabilité \(\frac{1}{8}\)
• un enfant avec une probabilité \(\frac{3}{8}\)
• deux enfants avec une probabilité \(\frac{3}{8}\)
• trois enfants avec probabilité \(\frac{1}{8}\) .

Les nombres d’enfants d’individus différents sont de plus supposés indépendants les
uns des autres, et on admet qu’aucun individu n’a plus de 3 enfants.

Voici un exemple d’arbre généalogique obtenu par ce procédé, en partant d’un ancêtre unique :

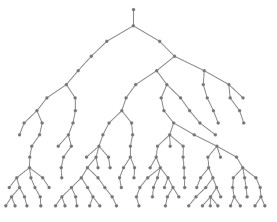
L’ancêtre, en haut de l’arbre, a un enfant, qui en a lui-même deux, et ainsi de suite.
Nous allons calculer la probabilité que la descendance d’un unique ancêtre s’éteigne.

Première partie : calculs de probabilités

Partons d’un seul individu. Nous étudions la population de ses descendants. La probabilité que la population s’éteigne dés la première génération (ses enfants) est \(q_1=\frac{1}{8}\) : il n’a pas d’enfant.
1. Cherchons d’abord la probabilité que la population soit éteinte à la deuxième
génération (il n’a pas d’enfant, ou il a des enfants mais pas de petits-enfants).
a) S’il a 2 enfants, quelle est la probabilité qu’il n’ait pas de petits-enfants ? Et s’il en a 3 ?
b) Calculer alors la probabilité que la population soit éteinte à la deuxième génération.
2. Soit \(q_n\) la probabilité pour que la descendance d’un individu comporte au plus n générations (n ≥ 1). Exprimer en fonction de \(q_n\) la probabilité \(q_{n+1}\) que la descendance d’un individu comporte au plus n + 1 générations. Pour calculer \(q_{n+1}\), on remarquera que la descendance d’un individu comporte au plus n + 1
générations s’il n’a pas d’enfant ou si les descendances de ses enfants comportent au plus n générations.

Deuxième partie : Étude de la suite (\(q_n\))

1. Soit f la fonction définie sur l’intervalle [0 ; 1], telle que :

$$q_{n+1}=f(q_n)$$

On aura montré plus haut que \(f(x)=\frac{1}{8} x^3+\frac{3}{8} x^2+\frac{3}{8} x+\frac{1}{8}\)
a) Étudier les variations de f sur l’intervalle [0 ; 1].
b) Pour comparer \(q_n\) et \(q_{n+1}\), on va étudier le signe de la fonction g définie sur l’intervalle [0 ; 1] par : \(g(x) = f (x) - x\).
On remarque que g s’annule en 1 ; ce polynôme se factorise alors par
(x - 1) : trouver a, b, c tels que \(g(x) = (x - 1)(ax^2 + bx + c).\)
En déduire le signe de g(x) sur l’intervalle [0 ; 1].
2. Étudions à présent la suite (\(q_n)\).
a) À l’aide du graphique ci-dessous, représenter les premiers termes de la suite (\(q_n\)). Que peut-on prédire sur son comportement ?

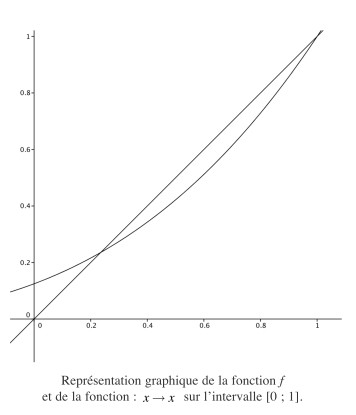
b) Démontrons les conjectures établies d’après le graphique :
Prouver par récurrence que pour tout entier n supérieur ou égal à 1 :

$$0 \le q_n \le \sqrt 5 - 2.$$

Prouver que la suite (\(q_n\)) est croissante.
c) Prouver que la suite (\(q_n\)) est convergente. Trouver sa limite (on utilisera la relation : \(q_{n+1}= f(q_n)\)).

Conclusion : on a ainsi prouvé que, sous nos hypothèses simplificatrices, la probabilité d’extinction de cette descendance d’un unique ancêtre est égale à \(\sqrt 5 - 2\) soit environ 23,6%.

II. Quelques commentaires

Le problème ne me semble pas adapté pour être exploité comme situation de découverte : l’arbre qu’on y voit dessiné n’est pas un arbre de probabilité, et l’arbre de probabilité que l’élève pourra construire pour résoudre la partie 1 n’est pas un arbre généalogique descendant. La difficulté de l’exercice réside précisément, il me
semble, dans ces deux représentations en arbre qui éclairent la situation, mais peuvent aussi la compliquer par leur coexistence. Il peut embrouiller les idées d’un
débutant et lui faire apparaître les arbres comme un objet bien redoutable !

Pour des élèves plus aguerris, son intérêt est de faire apparaître de façon naturelle une
suite définie par récurrence, et d’utiliser de façon non artificielle les quelques outils
dont disposent les élèves de Terminale S pour résoudre le problème.

Ils pourront ainsi trouver dans ce problème, en acte, un élément de réponse à la
question classique qu’il ne faut pas éluder : « À quoi servent les mathématiques ? ».

C’est une occasion à ne pas laisser passer !

<redacteur|auteur=500>