Le paiement intégral des impôts

Michel Lafond [1]

Le but de cet article est de proposer quelques formules simples de calcul de l’impôt, qui respectent la progressivité du taux d’imposition en fonction du revenu, sans avoir les inconvénients du système actuel qui, avec son système de tranches, n’est pas d’un maniement facile.

Il faut dire que l’impôt sur le revenu des personnes physiques (IRPP) a été mis en place durant la Première Guerre mondiale. Il n’y avait pas de calculettes à cette époque, mais maintenant elles sont omniprésentes, et on peut souhaiter exprimer l’impôt en fonction du revenu à l’aide d’une fonction élémentaire unique, même si les contraintes sont fortes sur les modalités.

Le nombre de thèmes utilisés fait qu’on peut aborder cet article de la seconde à la terminale :

Les fonctions affines par morceaux en seconde.
Les systèmes linéaires en première.
La continuité, la dérivabilité, l’intégration, la convexité, le comportement asymptotique des fonctions à l’infini, les courbes paramétrées en terminale ES ou S.

Le paragraphe 4 en particulier est une mine inépuisable de recherches.

1. Rappel du principe du taux d’imposition par tranches

Si on décide comme c’est l’usage chez nous, que les revenus seront découpés en tranches :

$$[a_0 , a_1[ ; [a_1 , a_2[ ; [a_2 , a_3[ ... [a_n , +\infty[$$

et que la tranche $T_i = [a_{i-1} , a_i[$ sera imposée au taux $t_i$, cela signifie qu’un individu ayant le revenu $R \ge 0$ paiera l’impôt I(R) calculé ainsi :

Il existe $i \ge 1$ unique tel que $a_{i-1} \le R < a_i$ (i est le numéro d’ordre de la tranche de R),
et alors

$$I(R) = (a_1 - a_0) × t_1 + (a_2- a_1) × t_2 + …+ (a_{i-1} - a_{i-2}) × t_{i-1} + (R - a_{i-1}) × t_i.$$

Ceux qui ont traité cette question avec des élèves savent la difficulté qu’ont ceux-ci devant ce genre de formule.

L’expression ci-dessus dit que le taux $t_i$ s’applique seulement à la tranche $T_i$. On ne le répètera jamais assez, car contrairement à une idée reçue (donc tenace), si le revenu R est dans la tranche $T_i$, le taux $t_i$ ne s’applique pas à la totalité de R mais uniquement
à la « portion » du revenu comprise dans la tranche $T_i$. [Nous verrons des exemples numériques dans le paragraphe suivant].

En ce qui concerne les unités :
R est en euros mais, par commodité, nous prendrons dans tous les exemples traités le millier d’euros ;
le taux t est un nombre décimal positif, il est sans dimension (comme disent les physiciens) et donc le montant de l’impôt I(R) s’exprime dans la même unité que R.
Nous omettrons l’unité dans toute la suite.

2. Un exemple

Supposons qu’il y ait quatre tranches de revenus taxées à l’aide du tarif progressif f ci-dessous :

Tranche de revenu R	Taux d’imposition de la tranche R : f(R)
[0 ; 10[	0
[10 ; 30[	0,01
[30 ; 60[	0,02
[60 ; +$\infty$[	0,03

Le tarif f est une fonction en escalier.
Le rapport entre la fonction tarif f et la suite t du paragraphe précédent est le suivant :
sur $[a_{i-1}, a_i[$, f est constante et vaut $t_i$.
L’introduction d’une fonction définie sur $\mathbb R^+$ est nécessaire pour les calculs d’intégrales qui vont suivre.

Pour le calcul de l’impôt, on a, avec les données ci-dessus, par exemple :
si R = 9 (première tranche), alors

$$I (9) = 9 \times 0 = 0.$$

si R = 29 (deuxième tranche), alors

$$I (29) = (10 - 0) \times 0 + (29 - 10) \times 0,01 = 0,19.$$

si R = 31 (troisième tranche), alors

$$I (31) = (10 - 0) \times 0 + (30 - 10) \times 0,01 + (31 - 30) \times 0,02 = 0,22.$$

Répétons que, contrairement à l’idée reçue précitée, il n’y a pas de saut (de discontinuité) dans le montant de l’impôt lorsqu’on change de tranche. C’est seulement dans le taux d’imposition qu’il y a discontinuité.
On pourrait demander à des élèves de terminale de montrer la continuité de I en R = 30 par exemple.

Quelle est l’expression analytique de I(R) ?
Si R $\in$ [0 ; 10[, alors

$$I(R) = R \times 0 = 0.$$

Si R $\in$ [10 ; 30[, alors

$$I(R) = (10 - 0) \times 0 + (R - 10) \times 0,01 = 0,01 R - 0,1.$$

Si R $\in$ [30 ; 60[, alors

$$I(R) = (10 - 0) \times 0 + (30 - 10) \times 0,01 + (R - 30) \times 0,02 = 0,02 R - 0,4.$$

Si R $\in$ [60 ; +$\infty$[, alors

$$I(R) = (10 - 0) \times 0 + (30 - 10) \times 0,01 + (60 - 30) \times 0,02 + (R - 60) \times 0,03 = 0,03 R - 1.$$

Remarque :
Ce sont des formules de ce genre qui sont utilisées dans le calcul de nos impôts.
Ainsi au paragraphe 5 de la fiche 2041-NOTFC de calculs facultatifs des impôts portant sur les revenus de 2006, fiche que tout le monde a reçue avec les feuilles de déclaration, ou qu’on peut consulter sur www.impôts.gouv.fr en cliquant sur Calcul et sur Voir la liste des formulaires, puis en sélectionnant la fiche 2041-NOTFC. On
peut y lire :

Si votre QF n’excède pas 5 614 €,

votre impôt € sera égal à 0.

Si votre QF est supérieur à 5 614 € et n’excède pas 11 198 €,

votre impôt € sera égal à R × 0,055 − 308,77 × N.

Si votre QF est supérieur à 11 198 € et n’excède pas 24 872 €,

votre impôt € sera égal à R × 0,14 − 1 260,60 × N.

Si votre QF est supérieur à 24 872 € et n’excède pas 66 679 €,

votre impôt € sera égal à R × 0,30 − 5 240,12 × N.

Si votre QF est supérieur à 66 679 €,

votre impôt € sera égal à R × 0,40 − 11 908,02 × N.

Ici, QF = R/N est le quotient familial, quotient du revenu imposable R par le nombre N de parts.
Les paliers de la fonction en escalier f donnant les taux d’imposition par tranches étaient donc en 2006 égaux à 0 ; 0,055 ; 0,14 ; 0,30 et 0,40.

Sur [0 ; +$\infty$[ la fonction I est affine par morceaux, et, là où elle est dérivable, on
remarque que sa dérivée est la fonction en escalier f égale au taux d’imposition par tranche.

Plus précisément on a : I’(R) = f(R) et I(R)=$\int_{0}^R f(t)\ dt$

Eh oui ! Le montant de l’impôt se calcule par une intégrale de Riemann, et on retrouve ainsi automatiquement la continuité de la
fonction I.

Pour terminer avec cet exemple, regardons les deux interprétations graphiques de l’impôt I(R) avant et après l’intégration :

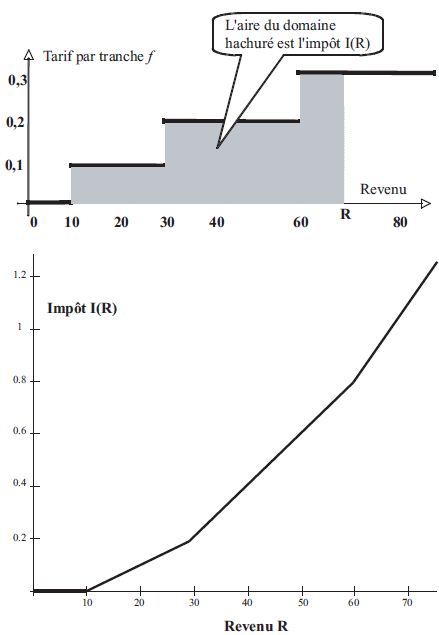
Tous ceux qui ont réfléchi à ce qui précède, se sont un jour ou l’autre demandé si on ne pourrait pas trouver une formule simple pour calculer l’impôt.

Plus simple dans le sens où on n’aurait pas besoin de tableau comme pour la fonction I de l’exemple précédent qui, on l’a vu, est définie par :

Tranche de revenu R	Montant de l’impôt I(R)
[0 ; 10[	0
[10 ; 30[	0,01 R − 0,1
[30 ; 60[	0,02 R − 0,4
[60 ; +$\infty$[	0,03 R − 1

3. Recherche d’une formule unique

On peut utiliser un résultat disant que les fonctions affines par morceaux définies et continues sur $\mathbb R$ peuvent toujours s’exprimer sous la forme

$$\varphi(x)=\alpha x +\beta + \Sigma \ c_i|x-x_i|$$

où les $x_i$ sont les abscisses des points anguleux (figure ci-dessous).

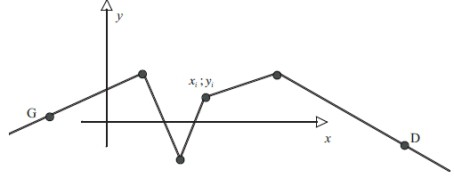
Les n + 2 inconnues de l’équation : $\alpha, \beta, c_i$ (i = 1, …,n) se calculent en résolvant le système linéaire obtenu en écrivant que la courbe passe par :
– un point G quelconque sur la branche gauche,
– un point D quelconque sur la branche droite,
– les n points anguleux $M_i (x_i ; y_i)$.

Ici, dans l’exemple très simple du paragraphe 2, cela donne :

$$I(R) = \alpha R + \beta + c_1 |R - 10| + c_2 |R - 30| + c_3 |R - 60|.$$

Les cinq inconnues se calculent en écrivant que la courbe passe par les cinq points
(0 ; 0) (10 ; 0) (30 ; 0,2) (60 ; 0,8) et (100 ; 2).
La résolution (une simple calculette suffit) du système linéaire qui en résulte :

$$\left\{\begin{array}{rcl} \beta + 10c_1 + 30c_2 + 60c_3=0\\ 10\alpha + \beta +20c_2 + 50c_3=0\\ 30\alpha + \beta + 20c_1 + 30c_3=0,2\\ 60\alpha + \beta +50 c_1 + 30c_2 =0,8\\ 100\alpha + \beta + 90c_1 + 70c_2 + 40c_3=2\\ \end{array}\right$$

donne :

I(R) = ${1 \over 200}(3 R-100+|R-10|+|R-30|+|R-60|)$

On a bien une formule unique, mais toujours les point anguleux !

4. Passage à un modèle à taux continu

On aimerait une courbe sans points anguleux, en particulier un « démarrage en douceur » de l’impôt, c’est-à-dire I’(m) = 0 où m est le revenu « plancher » en dessous duquel on ne paie pas d’impôt.

Énonçons donc le cahier des charges d’un modèle dérivable du montant de l’impôt, susceptible de faire le bonheur des contribuables mathématiciens :

CAHIER DES CHARGES

Soient

m le revenu « plancher » en dessous duquel on ne paie pas d’impôt.

0 < a $\le$ 1 le taux maximal d’imposition.

On veut une fonction I définie sur [0 ; +$\infty$[ et telle que :

C1. I est nulle sur [0 ; m],

C2. I est croissante, et dérivable,

C3. I est convexe puisqu’on souhaite un tarif f = I’ progressif,

C4. I’(m) = 0 pour un démarrage en douceur,

C5. Pour tout R $\ge$ 0, I(R) $\le$ aR et, pour les gros revenus, I(R) $\approx$ aR.

Remarque : la condition I(R) $\le$ aR traduisant le fait que a est le taux maximal d’imposition découle des autres conditions puisque :
Si R $\le$ m, alors I(R) = 0 $\le$ aR.
Si R > m, alors I’(R) = f (R) $\le$ a (taux maximal d’imposition) implique

$$I(R)=\int_{m}^R f(t)\ dt \le \int_{m}^R a\ dt=a(R-m) \le aR$$

Avec I(R) = ${1 \over 200}(3 R-100+|R-10|+|R-30|+|R-60|)$, les conditions C2 et C4 ne sont pas entièrement vérifiées. Cherchons autre chose.

Un polynôme peut-être ?
La contrainte I(R) $\approx$ aR de la condition C5 implique que le polynôme soit de degré 1, c’est-à-dire I(R) = aR + b, ce qui est incompatible avec la condition I’(m) = 0 puisque cela entraînerait a = 0 !
Le taux d’imposition serait nul. On peut rêver.
Et si on faisait appel à l’exponentielle ?
La contrainte I(R) $\approx$ aR de la condition C5 suggère de prendre à partir de R = m un impôt de la forme $I(R) = {a}R- ke^{-R}$ avec k constant positif pour avoir I(R) $\le$ aR.
On aurait alors $I’(R) = a + k e^{-R} > 0$ ce qui satisfait la condition C2.
Mais $I’’(R) = −{k} e^{-R} < 0$ est en contradiction avec la convexité.

On peut essayer $I(R) = a R (1 - k e^{-R})$ mais, là encore, c’est un bon exercice de
montrer qu’on ne peut pas satisfaire complètement le cahier des charges.

Une possibilité qui aboutit est : à partir de R = m prendre $I(R) = a (R + b + k e^{-R})$, b, k constants.
On aurait $I’(R) = a (1 - k e^{-R}).$
La condition I’(m) = 0 implique $k = e^m$ et alors $I’(R) = a (1 - k e^{m-R}).$
C2 et C4 sont vérifiées.
$I’’(R) = a e^{m-R}$ > 0 garantit la convexité donc C3.
I(m) = 0 implique a (m + b + 1) = 0, donc b = − (m + 1),

$$soit \ I(R) = a [R - (m + 1) + e^{m-R}].$$

Il faut encore vérifier que pour tout R $\ge$ 0, I(R) $\le$ aR :
Jusqu’à R = m, I(R) = 0 $\le$ aR et, à partir de R = m, $e^{m-R} \le 1$ implique

$$I(R) \le a [R - m] \le a R.$$

On a une première solution :

I(R)=0 sur [0 ;m]

$I(R)=a[R-(m+1)+e^{m-R}]$ sur [m ;+$\infty$[

Mais la courbe représentative visible à la fin montre que la « progressivité » souhaitée pour l’impôt est à peu près inexistante.

Finalement, pourquoi ne pas se contenter des fonctions rationnelles ?
On pense alors au modèle simple et naturel :

$$I(R)=0 \text{ sur } [0 ;m]$$

$$I(R)=aR-b+{k \over R} \text{ pour } R>m$$

pour lequel C1 et une partie de (C2, C5) sont déjà vérifiés, en particulier I(R)$\approx$ aR.
La dérivée première vaut $I’(R)=f(R)=a-{k \over R^2}$
I sera convexe si k est positif car la dérivée seconde de I vaut $I’’(R)={2k \over R^3}$
Or k est imposé par la condition C4 du cahier : I’(m) = 0 entraîne $k = a m^2$ qui est positif.
La continuité de I impose I(m) = 0 c’est-à-dire a m − b + a m = 0 d’où b = 2 a m.
On a donc nécessairement :
$$I(R)=aR-2am+{am^2 \over R}=aR\left( 1-{m \over R}\right)^2 si \ R>m$$

La solution unique à ce modèle est :

I(R)=0 sur [0 ;m]

$I(R)=aR\left( 1-{m \over R}\right)^2$ sur [m ;+$\infty$[

On vérifie sans peine les cinq conditions du cahier des charges.

En particulier, si R > m : $I’(R)=a\left( 1-{m^2 \over R^2}\right)$ > 0 et $I’’(R)={2am^2 \over R^3}$ >0.

5. Comparaison du modèle à taux discret et des modèles à taux
continus

Avec m = 10 et a = 0,03 traçons dans un même repère les courbes des trois fonctions :

$I_D$ pour le modèle discret du paragraphe 2 :
$$I(R) = {1 \over 200}(3 R-100+|R-10|+|R-30|+|R-60|)$$
$I_E$ pour le modèle exponentiel :
$$I_E(R)=0 \ \ sur \ \ [0 ;10]$$

$$I_E(R)=0,03[R-11+e^{10-R}] \ \ sur \ \ [10 ;+\infty[$$
$I_2$ pour le modèle « rationnel » qu’on vient de voir à la fin du paragraphe 4 :
$$I_2(R)=0 \ \ sur \ \ [0 ;10]$$

$$I_2(R)=0,03R\left( 1-{10 \over R} \right)^2 \ \ sur \ \ [10 ;+\infty[$$

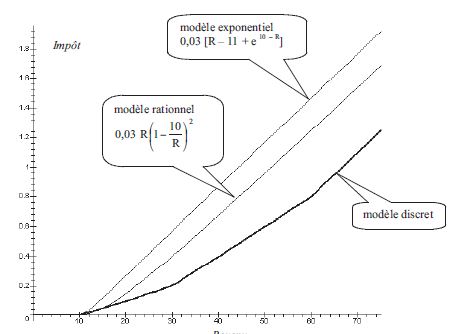
On voit bien les défauts mentionnés plus haut du modèle exponentiel : très faible convexité, de plus le démarrage en douceur pour R = 10 n’est visible que sur un zoom !

Le modèle rationnel démarre en douceur mais présente pour les gros revenus un biais systématique.

Si on s’intéresse un peu plus aux gros revenus, on peut chercher les développements limités d’ordre 1 à l’infini des trois formes I (R) précédentes. Ce sont :

0,03R−1 pour le modèle discret

0,03[R−11]=0,03R−0,33 pour le modèle exponentiel

0,03R−0,6 pour le modèle rationnel

C’est évident pour les deux premiers, et pour le troisième 0,03 R − 0,6 provient de :

$$0,03R \left( 1-{10 \over R} \right)^2=0,03R \left( 1-{20 \over R}+ {100 \over R^2} \right)=0,03R-0,6+{3 \over R}$$

Le modèle rationnel semble prometteur pour des améliorations.
Voyons comment.

6. Extension par introduction d’un paramètre.

Le modèle :

$$I_\lambda (R)=0 \ \ sur \ \ [0 ;m],$$

$$I_\lambda (R)=aR \left( 1-{m \over R} \right)^\lambda \ \ sur \ \ [m ;+\infty],$$

semblable au modèle rationnel précédent mais avec un exposant $\lambda \ge 2$ convient-il ?

Oui, puisqu’on vérifie sans peine que si R > m :
$I’_\lambda (R)=a \left( {R+m(\lambda-1) \over R} \right) \left( 1-{m \over R} \right) ^\lambda$ est positive,
et $I’’_\lambda (R)=f’(R)={a \over R^3} \left( 1-{m \over R} \right) ^{\lambda-2} \left( m^2(\lambda-1)^2 \right) $ est aussi positive, donc le tarif est progressif.

La condition C5 est manifestement vérifiée, le cahier des charges est respecté.

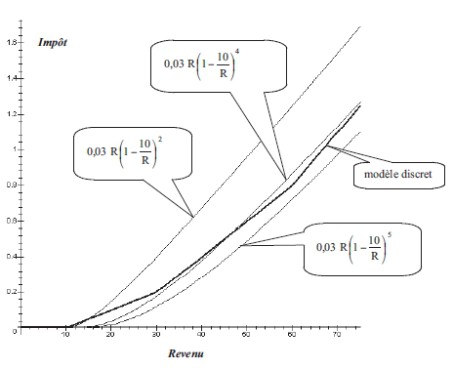
À la page suivante, on peut voir les courbes de $I_2, \ de \ I_4 \ et \ de \ I_5$ (modèle rationnel pour $\lambda$ = 2, $\lambda$ = 4, $\lambda$ = 5) et observer l’évolution de leur ajustement par rapport au modèle
discret.
On peut même choisir le paramètre $\lambda$ pour que le modèle discret et le modèle $I_\lambda$ aient des courbes asymptotes à l’infini (exercice laissé au lecteur).

7. Conclusion

Cette étude technique n’est qu’un élément de réflexion et ne prétend pas être une argumentation politique ou économique sur la justice ou l’efficacité de l’impôt.