Gabriel Peyré [1]

Résumé. Les appareils numériques photographient de manière très précise le monde qui nous entoure. L’utilisateur souhaite pouvoir stocker avec un encombrement minimal ses photos sur son disque dur. Il souhaite également pouvoir les retoucher afin d’améliorer leur qualité. Cet article présente les outils mathématiques et informatiques qui permettent d’effectuer ces différentes tâches. Il reprend en partie le contenu de l’article publié sur le site web Images des mathématiques [2] .

1. Les pixels d’une image

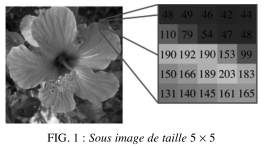
Une image numérique en niveaux de gris est un tableau de valeurs. Chaque case de ce tableau, qui stocke une valeur, se nomme un pixel. En notant n le nombre de lignes et p le nombre de colonnes de l’image, on manipule ainsi un tableau de $n \times p$ pixels. La figure 1, gauche, montre une visualisation d’un tableau carré avec n = p = 240, ce qui représente $240 \times 240 = 57 600 $ pixels. Les appareils photos numériques peuvent enregistrer des images beaucoup plus grandes, avec plusieurs millions de pixels.
Les valeurs des pixels sont enregistrées dans l’ordinateur ou l’appareil photo numérique sous forme de nombres entiers entre 0 et $255 = 2^8 - 1$, ce qui fait 256 valeurs possibles pour chaque pixel. La valeur 0 correspond au noir, et la valeur 255 correspond au blanc. Les valeurs intermédiaires correspondent à des niveaux de gris allant du noir au blanc. La figure 1 montre un sous-tableau de $5 \times 5$ pixels extrait de l’image précédente. On peut voir à la fois les valeurs qui composent le tableau et les niveaux de gris qui permettent d’afficher l’image à l’écran.

2. Stocker une image

2.1. Écriture binaire

Stocker de grandes images sur le disque dur d’un ordinateur prend beaucoup de place. Les nombres entiers sont stockés en écriture binaire, c’est-à-dire sous la forme d’une succession de 0 et de 1. Chaque 0 et chaque 1 se stocke sur une unité élémentaire de stockage, appelée bit. Pour obtenir l’écriture binaire d’un pixel ayant comme valeur 179, il faut décomposer cette valeur comme somme de puissances de deux. On obtient ainsi

$$179 = 2^7 + 2^5 + 2^4 + 2 + 1,$$

où l’on a pris soin d’ordonner les puissances de deux par ordre décroissant. Afin de faire mieux apparaître l’écriture binaire, on ajoute « 1 $\times$ » devant chaque puissance qui apparaît dans l’écriture, et « 0 $\times$ » devant les puissances qui n’apparaissent pas

$$179 = 1 \times2^7 + 0 \times2^6 +1 \times2^5 + 1 \times2^4 + 0 \times2^3 + 0 \times2^2+1 \times 2^1 + 1 \times 2^0.$$

Avec une telle écriture, la valeur de chaque pixel, qui est un nombre entre 0 et 255, nécessite $log_2(256) = 8$ bits. La fonction $log_2$ est le logarithme en base 2, et ce calcul exprime le fait que $256 = 2^8$ . L’écriture binaire de la valeur 179 du pixel est ainsi (1, 0, 1, 1, 0, 0, 1, 1), où chaque 1 et chaque 0 correspond au facteur multiplicatif qui apparaît devant chaque puissance.

On peut écrire toute valeur entre 0 et 255 de cette manière, ce qui nécessite l’utilisation de 8 bits. Il y a en effet 256 valeurs possibles, et $256 = 2^8$ . Pour stocker l’image complète, on a donc besoin de $n \times p \times 8$ bits. Pour l’image montrée aux figure précédentes, on a ainsi besoin de $240 \times 240 \times 8 = 460 800$ bits.
On utilise le plus souvent l’octet (8 bits) comme unité, de sorte que cette image nécessite 57,6 ko (kilo octets).

2.2. Sous-échantilloner une image

Afin de réduire la place de stockage d’une image on peut diminuer le nombre de pixels. La façon la plus simple d’effectuer cette réduction consiste à supprimer des lignes et des colonnes dans l’image de départ. La figure 2, à gauche, montre ce que l’on obtient si l’on retient une ligne sur 4 et une colonne sur 4. On a ainsi divisé par
$4 \times 4 = 16$ le nombre de pixels de l’image, et donc également réduit par 16 le nombre de bits nécessaire pour stocker l’image sur un disque dur. Sur la figure 2, on peut voir les résultats obtenus en enlevant de plus en plus de lignes et de colonnes. Bien entendu, la qualité de l’image se dégrade vite.

2.3. Quantifier une image

Une autre façon de réduire la place mémoire nécessaire pour le stockage consiste à utiliser moins de nombres entiers pour chaque valeur. On peut par exemple utiliser uniquement des nombres entiers entre 0 et 3, ce qui donnera une image avec uniquement 4 niveaux de gris. On peut effectuer une conversion de l’image d’origine
vers une image avec 3 niveaux de valeurs en effectuant les remplacements :

• les valeurs dans 0, 1, …, 63 sont remplacées par la valeur 0,
• les valeurs dans 64, 65, …, 127 sont remplacées par la valeur 1,
• les valeurs dans 128, 129, …, 191 sont remplacées par la valeur 2,
• les valeurs dans 192, 193, …, 255 sont remplacées par la valeur 3.
  Une telle opération se nomme quantification. La figure 3, au centre, montre l’image résultante avec 4 niveaux de couleurs. Les 4 valeurs sont affichées en utilisant 4 niveaux de gris allant du noir au blanc.

Nous avons déjà vu que l’on pouvait représenter toute valeur entre 0 et 255 à l’aide de 8 bits en utilisant l’écriture binaire. De façon similaire, on vérifie que toute valeur entre 0 et 3 peut se représenter à l’aide de 2 bits. On obtient ainsi une réduction d’un facteur 8/2 = 4 de la place mémoire nécessaire pour le stockage de l’image sur un disque dur. La figure 3 montre les résultats obtenus en utilisant de moins en moins de niveaux de gris.

Tout comme pour la réduction du nombre de pixels, la réduction du nombre de niveaux de gris influe beaucoup sur la qualité de l’image. Afin de réduire au maximum la taille d’une image sans modifier sa qualité, on utilise des méthodes plus complexes de compression d’image. L’article « Matrices et images numériques » paru dans le Bulletin 500 détaille une méthode qui exploite la décomposition en
valeurs singulières des matrices.

3. Enlever le bruit

3.1. Moyenne locale

Les images sont parfois de mauvaise qualité. Un exemple typique de défaut est le bruit qui apparait quand
une photo est sous-exposée, c’est-à-dire qu’il n’y a pas assez de luminosité. Ce bruit se manifeste par de petites
fluctuations aléatoires des niveaux de gris. La figure ci-contre montre une image bruitée.

Afin d’enlever le bruit dans les images, il convient de faire subir une modification aux valeurs de pixels. L’opération la plus simple consiste à remplacer la valeur a de chaque pixel par la moyenne de a et des 8 valeurs b, c, d, e, f, g, h, i des 8 pixels qui entourent a. La figure 4 montre un exemple de voisinage de 9 pixels. On obtient ainsi une image modifiée en remplaçant a par

$$\frac{a+b+c+d+e+f+g+h+i}{9}$$

puisque l’on fait la moyenne de 9 valeurs. Dans notre exemple, cette moyenne vaut

$$\frac{190+192+79+54+47+153+203+189+166}{9}\approx 141.4.$$

En effectuant cette opération pour chaque pixel, on supprime une partie du bruit, car ce bruit est constitué de fluctuations aléatoires, qui sont diminuées par un calcul de moyennes. La figure 5, à gauche, montre l’effet d’un tel calcul. Tout le bruit n’a pas été enlevé par cette opération. Afin d’enlever plus de bruit, on peut moyenner plus de valeurs autour de chaque pixel. La figure 5 montre le résultat obtenu en moyennant de plus en plus de valeurs.

Le moyennage des pixels est très efficace pour enlever le bruit dans les images, malheureusement il détruit également une grande partie de l’information de l’image. On peut en effet s’apercevoir que les images obtenues par moyennage sont floues.
_Ceci est en particulier visible près des contours, qui ne sont pas nets.

3.2. Médiane locale

Afin de réduire ce flou, il faut remplacer le moyennage par une opération un peu plus complexe, que l’on nomme médiane. Etant donné la valeur a d’un pixel, et les valeurs b, c, d, e, f, g, h, i, on commence par les classer par ordre croissant. Dans l’exemple du voisinage de 9 pixels utilisé à la section précédente, on obtient les 9 valeurs classées

$$47, 54, 79, 153, 166, 189, 190, 192, 203.$$

La médiane des neuf valeurs a, b, c, d, e, f, g, h, i est la cinquième valeur de ce classement (c’est-à-dire la valeur centrale de ce classement).

Dans notre cas, la médiane est donc 166. Notez que ce nombre est en général différent de la moyenne, qui vaut pour notre exemple 141,4. Afin d’enlever plus de bruit, il suffit de calculer la médiane sur un nombre plus grand de pixels voisins, comme montré à la figure 6. On constate que cette méthode est plus performante que
le calcul de moyennes, car les images résultantes sont moins floues. Cependant, tout comme avec le calcul de moyennes, si l’on prend des voisinages trop grands, on perd aussi de l’information de l’image, en particulier les bords des objets sont dégradés.

4. Détecter les bords des objets

Afin de localiser des objets dans les images, il est nécessaire de détecter les bords de ces objets. Ces bords correspondent à des zones de l’image où les valeurs des pixels changent rapidement. C’est le cas par exemple lorsque l’on passe de la coque du bateau (qui est sombre, donc avec des valeurs petites) à la mer (qui est claire, donc avec des valeurs grandes).

Afin de savoir si un pixel avec une valeur a est le long d’un bord d’un objet, on prend en compte les valeurs b, c, d, e de ses quatre voisins (deux horizontalement et deux verticalement), qui sont disposés par rapport à a comme illustré à la figure 7.

Notons que l’on utilise ici seulement les 4 voisins qui ont un coté commun avec le pixel considéré, ce qui est différent du calcul de moyennes et de médianes où l’on utilisait 8 voisins. Ceci est important afin de détecter aussi précisément que possible les bords des objets.

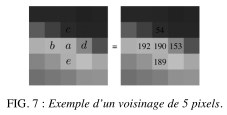
On calcule une valeur $\ell$ suivant la formule

$$\ell=\sqrt{(b-d)^2+(c-e)^2}$$

Dans notre exemple, on obtient donc

$$\ell=\sqrt{(192-153)^2+(189-54)^2}=\sqrt{19746}\approx140.5$$

On peut remarquer que si $\ell = 0$, alors on a b = c et d = e. Au contraire, si $\ell$ est grand, ceci signifie que les pixels voisins ont des valeurs très différentes, le pixel considéré est donc probablement sur le bord d’un objet.
La figure 8 montre une image dont la valeur des pixels est min( , 255). On a ainsi affiché ces valeurs avec du noir quand = 0, du blanc quand est grand, et on a utilisé des niveaux de gris pour les valeurs intermédiaires. On peut voir que dans l’image de droite, les contours des objets ressortent en blanc, car ils correspondent
aux grandes valeurs de $\ell$ .

5. Les images couleurs

5.1. Espace RVB

Une image couleur est en réalité composée de trois images indépendantes, afin de représenter le rouge, le vert, et le bleu. Chacune de ces trois image s’appelle un canal. Cette représentation en rouge, vert et bleu mime le fonctionnement du système visuel
humain. La figure 10 montre les trois canaux constitutifs de l’image montrée sur la gauche de la figure 9.

Chaque pixel de l’image couleur contient ainsi trois nombres (r, v, b), chacun étant un nombre entier entre 0 et 255. Si le pixel est égal à (r, v, b) = (255, 0, 0), il ne contient que de l’information rouge, et est affiché comme du rouge. De façon similaire, les pixels valant (0, 255, 0) et (0, 0, 255) sont respectivement affichés vert et bleu.

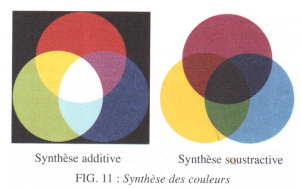
On peut afficher à l’écran une image couleur à partir de ses trois canaux (r, v, b) en utilisant les règles de la synthèse additive des couleurs. Ces règles correspondent à la façon dont les rayons lumineux se combinent, d’où le qualificatif « additif ». La figure 11, gauche, montre les règles de composition de cette synthèse additive des couleurs. Par exemple un pixel avec les valeurs (r, v, b) = (255, 0, 255) est un mélange de rouge et de vert, il est donc affiché comme du jaune.

5.2. Espace CMJ

Une autre représentation courante pour les images couleurs utilise comme couleurs de base le cyan, le magenta et le jaune. On calcule les trois nombres (c, m, j) correspondant à chacun de ces trois canaux à partir des canaux rouge, vert et bleu (r, v, b) comme suit

$$c = 255 - r, m = 255 - v, j = 255 - b.$$

Par exemple, un pixel de bleu pur (r, v, b) = (0, 0, 255) va devenir (c, m, j) = (255, 255, 0). La figure suivante montre les trois canaux (c, m, j) d’une image couleur.

Afin d’afficher une image couleur à l’écran à partir des trois canaux (c, m, j), on doit utiliser la synthèse soustractive des couleurs. La figure 11, droite, montre les règles de composition cette synthèse soustractive. Elle correspondent en peinture à l’absorption de la lumière par les pigments colorés, d’où le qualificatif « soustractif ». Le cyan, le magenta et le jaune sont appelés couleurs primaires.

On peut donc stocker sur un disque dur une image couleur en stockant les trois canaux, correspondant aux valeurs (r, g, b) ou (c, m, j). On peut modifier les images couleur tout comme les images en niveaux de gris. La façon la plus simple de procéder consiste à appliquer la modification à chacun des canaux.

6. Changer le contraste d’une image

6.1. Luminance

On peut calculer une image en niveaux de gris à partir d’une image couleur en moyennant les trois canaux. On calcule donc, pour chaque pixel, une valeur

$$a=\frac{r+v+b}{3}$$

qui s’appelle la luminance de la couleur. La figure 9 montre le passage d’une image couleur à une image de luminance en niveaux de gris.

6.2. Manipulations du contraste en niveaux de gris

Il est possible de faire subir différentes modifications à l’image afin de changer son contraste. On considère ici une image en niveaux de gris. Un manipulation simple consiste à remplacer chaque valeur a d’un pixel d’une image par 255 - a ce qui correspond à l’intensité de gris opposée. Le blanc devient noir et vice-et-versa, ce qui donne un effet similaire à celui des négatifs d’appareils photos argentiques, voir figure 13, gauche.

On éclaircit ou assombrit l’image en utilisant une fonction croissante de [0, 255] dans [0, 255] que l’on applique aux valeurs des pixels. On peut assombrir l’image en utilisant la fonction carré. Plus précisément, on définit la nouvelle valeur d’un pixel de l’image comme $a^2 /255$, voir figure 13, centre. Il est important d’effectuer la
division par 255 pour assurer que le résultat reste dans l’intervalle [0, 255]. Notons également que le résultat n’est en général plus un nombre entier. Afin de le stocker dans un fichier, il faut arrondir chaque valeur des pixels de l’image à l’entier le plus proche. Pour éclaircir l’image, on définit la nouvelle valeur d’un pixel de l’image comme $\sqrt{255a}$. La figure 13, droite montre l’éclaircissement obtenu. On pourra noter que ces deux opérations éclaircissement par carré et assombrissement par racine carrée) sont inverses l’une de l’autre.

6.3. Manipulations du contraste en couleur

Afin de manipuler le contraste d’une image couleur, il est important de respecter autant que possible les teintes des couleurs. On souhaite donc ne manipuler que la composante de luminance $a=\frac{r+v+b}{3}$ , en conservant constant le résidu
(r - a, v - a, b - a). On peut par exemple définir un changement de contraste en élevant la luminance a à la puissance $\gamma$> 0, afin d’obtenir $~{a}=255\times \left(\frac{a}{255}\right)^\gamma=255\times exp\left(\gamma \times ln\left(\frac{a}{255}\right)\right),$(avec la convention $~{a}$ = 0 lorsque a = 0). Comme $\gamma$ n’est pas nécessairement un nombre entier, il est important d’utiliser l’exponentielle et le logarithme pour définir ce changement. On remarque que pour $\gamma=1/2$ (respectivement $\gamma= 2$) on retrouve le changement de contraste par passage au carré (respectivement à la racine carrée) introduit à la section précédente. On constate également que pour $\gamma=1$, la luminance
est inchangée, i.e. $~{a}$= a.

Ce changement de contraste est ensuite répercuté sur l’image couleur en définissant trois canaux ($~{r},~{v},~{b}$) d’une nouvelle image par

$$ \left\{ {\begin {array}{rcl} \{~{r}&=&max(0,min(255,r+~{a}-a)\\\{~{v}&=&max(0,min(255,v+~{a}-a)\\\{~{b}&=&max(0,min(255,b+~{a}-a)\end{array}$$

Il est important de prendre le maximum avec 0 et le minimum avec 255 afin que le résultat reste dans l’intervalle [0, 255], et soit affiché de manière correcte. La figure 14 montre le résultat obtenu pour différentes valeurs de $\gamma$. Pour $\gamma$< 1, l’image est
éclaircie, alors que pour $\gamma$> 1, l’image est assombrie.

7. Images et matrices

7.1. Symétrie et rotation
Une image est un tableau de nombres, avec n lignes et p colonnes. Il est donc facile d’effectuer certaines transformations géométriques sur l’image. Les valeurs des pixels qui composent ce tableau (noté A) peuvent être représentées sous la forme A=($a_{i,j}$) où l’index i décrit l’ensemble des nombres 1, …, n (les entiers entre 1 et n) et l’index j les nombres 1, …, p. On dit que $a_{i,j}$ est la valeur du pixel à la position (i, j).

Le tableau de pixels ainsi indexé se représente de la façon suivante

ce qui montre que le pixel en haut à gauche de l’image correspond à la valeur $a_{1,1}$.
Ceci correspond à la représentation de l’image sous forme d’une matrice. Si l’on échange les lignes et les colonnes, on définit un autre tableau B avec p lignes et n colonnes. La formule qui définit le tableau B=($b_{j,i}$) est $b_{j,i}=a_{i,j}$. Ceci correspond à
la transposition de la matrice des pixels de l’image. Pour une image couleur, on effectue cette modification sur chacune de ses trois composantes couleur R, V et B.

La figure 15 montre l’image des tableaux A et B. La modification correspond à faire subir à l’image une symétrie par rapport à la diagonale qui joint le coin haut/gauche au coin bas/droite.

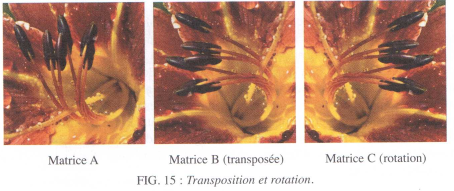
On peut également effectuer une rotation d’un quart de tour dans le sens des aiguille d’une montre à l’image. Ceci est obtenu en définissant une matrice C=($c_{i,j}$) de p lignes et n colonnes par $c_{i,j}=a_{n-i+1,j}$. La figure 15, droite, montre l’action de cette
rotation sur une image.

7.2. Fondu entres deux images
On souhaite effectuer une transition entre deux images A et B de même taille. On suppose donc que les deux images ont le même nombre n de lignes et le même nombre p de colonnes. On note les pixels de l’image A et les pixels de l’image B.
Pour une valeur t fixée entre 0 et 1, on définit l’image C=($c_{i,j}$) comme

$$c_{i,j}=(1-t)a_{i,j}+tb_{i,j}.$$

Il s’agit de la formule d’une interpolation linéaire entre les deux images. Pour une image couleur, on applique cette formule à chacun des canaux R, V et B.

On peut constater que pour t = 0, l’image C est égale à l’image A. Pour t = 1, l’image C est égale à l’image B. Lorsque la valeur t progresse de 0 à 1, on obtient ainsi un effet de fondu, puisque l’image, qui au départ est proche de l’image A ressemble de plus en plus à l’image B. La figure 16 montre le résultat obtenu pour 6
valeurs de t réparties entre 0 et 1.

Conclusion

Le traitement mathématique des images est un domaine très actif, où les avancées théoriques se concrétisent sous la forme d’algorithmes rapides de calcul. Ces algorithmes ont des applications importantes pour la manipulation des contenus
numériques. Cet article n’a cependant fait qu’effleurer l’immense liste des traitements que l’on peut faire subir à une image. L’article « Matrices et images numériques » paru dans le Bulletin 500 montre d’autres exemples de modifications que l’on peut effectuer sur des images. Les personnes intéressées pourront également
consulter le site web A Numerical Tour of Signal Processing [3] pour de nombreux
exemples de traitements d’images ainsi que des liens vers d’autres ressources disponibles en ligne.

<redacteur|auteur=500>