Joëlle Lamon [1]

Introduction

Au cours du temps se sont développés de nombreux jeux et défis liés aux alignements de points : problèmes de plantations d’arbres, de réseaux de points, mais aussi morpion, puissance 4, … Nous en proposons ici une analyse.

1. Approche historique

De tous temps, les alignements ont joué un rôle dans la culture humaine, comme le montrent bien des traces : ils sont présents à Carnac, à l’Ile de Pâques, en Corse, …
Ils se retrouvent encore actuellement dans des plantations, des dispositions d’arbres le long d’une route, de voitures dans un parking, de tombes dans un cimetière, …

Les traces les plus anciennes de jeux d’alignements et de blocages remontent au temple de Kurna (Égypte) en 1400 av. J.-C., mais aussi à Troie, en Grèce avec le « jeu du diagramme ».
On suppose que la marelle est née en Mésopotamie. Elle s’est diffusée à l’aide des Phéniciens : elle représentait pour eux la mer, Tyr au centre et ses colonies tout autour. On en trouve des traces jusqu’en Irlande. Elle s’est dissociée en deux types de jeu : le jeu physique faisant appel à la motricité, et le jeu contemplatif, statique faisant appel à la réflexion : le joueur est remplacé par les pions.

Au Moyen Âge, apparaissent les mérelles en France, le jeu du moulin en Allemagne, le nine men’s morris en Angleterre. On retrouve le principe du jeu : placer des pions et les déplacer éventuellement afin de constituer un alignement. La simplicité du jeu et des règles en font son caractère universel. Ce type de jeu s’appelle « Hirondelle d’or » en Mongolie, « Dris  » au Liban, « Hema  » en Côte d’Ivoire, « Mu-Torere » chez les Maoris en Nouvelle Zélande.

Plus tard, le Renju japonais et le Gomoku Ninuki où il faut aligner non plus trois pions mais cinq, sont revenus en Europe au XIXe siècle sous la forme du morpion.
Parallèlement à cela se sont développés des défis mathématiques, et ceci particulièrement à partir de la Renaissance. Plusieurs problèmes liés aux alignements
méritent d’être cités :

Problèmes d’alignements proposés par Dudeney

1. Dans une plantation carrée 7 × 7 où quatre cases sont inoccupées, il faut garder dix arbres de façon à pouvoir former cinq rangées de quatre arbres [2].

   

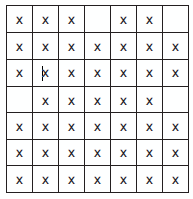
2. Dudeney a également analysé le problème des « différentes positions possibles pour 10 pièces de monnaie qui doivent former cinq alignements de quatre pièces », en nommant différentes solutions « star » (étoile), « dart » (fléchette), « compasses » (compas), « funnel », « scissors » (ciseaux), « nail » (ongle) [3]

3. 

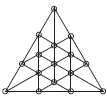
   Un châtelain du Sussex possédait une plantation de seize chênes, disposés de telle sorte qu’ils formaient douze alignements de quatre arbres. On demande comment faire pour les disposer en quinze rangées de quatre [4].

Une généralisation de ce problème est proposée par Sylvester (1814-1897) :
Problème du verger (1893)
Étant donnés n arbres tels que quatre d’entre eux ne soient jamais alignés, combien d’alignements de trois arbres peut-on avoir ?

Voici plusieurs solutions à ce problème, dont on ne connaît pas la solution générale :
1°) pour des alignements de 3 arbres :

Points	3	4	5	6	7	8	9	10	11	12
Alignements	1	1	2	4	6	7	10	12	16	19

2°) pour des alignements de 4 arbres

Points	3	4	5	6	7	8	9	10	11	12
Alignements	-	1	1	1	2	2	3	5	6	7

Des problèmes sont encore régulièrement proposés dans l’une ou l’autre revue s’intéressant aux jeux mathématiques.

2. Approche didactique

Les alignements considérés ici seront uniquement des dispositions sur une ligne droite.
Il existe de nombreux théorèmes et propriétés liés aux alignements, et rechercher si des points sont alignés est un exercice classique sur les fonctions affines et la géométrie analytique. Nous n’y reviendrons pas ici et vous proposons plutôt quelques « curiosités mathématiques ».

a) Quelques défis
Nous vous proposons de prendre ici le temps de réfléchir à quatre problèmes qui seront analysés plus loin.

1. Planter neuf arbres en formant dix alignements de trois arbres (Newton, 1643-1727).
2. Déplacer un pion pour avoir quatre rangées de trois pions alignés [5].

   

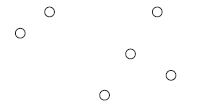
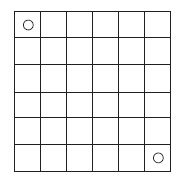
3. Dans un carré 8 × 8, placer huit pions de sorte qu’il n’y ait jamais deux pions sur une même ligne, une même colonne ou une même diagonale et que trois pions ne soient jamais alignés [6].

   

   b) Théorème de Sylvester (1893)
   En 1893, Sylvester a posé le problème suivant : « Est-il possible de dessiner un nombre fini de points de sorte que sur toute droite qui relie deux quelconques d’entre eux se trouve au moins un nouveau point de l’ensemble, sans que tous les points ne se trouvent sur une même droite ? » [7]
   La démonstration de l’impossibilité peut se faire facilement par l’absurde, en utilisant le concept de distance d’un point à une droite (Kelly, 1948) :

   Soit un ensemble fini E de points qui ne sont pas tous alignés et tels que toute droite reliant deux points quelconques de E comprend au moins un autre point de E. Le nombre de ces droites est fini (et vaut au maximum \(C_n^2\) ).

   Considérons l’ensemble F des paires (P,d) composées d’une droite d qui relie deux points de E et d’un point P de E extérieur à d, dont l’existence est assurée par le fait que les points de E ne sont pas tous alignés. Parmi les distances |Pd|, qui peuvent être ordonnées, considérons la distance minimale, correspondant à la paire (\(P_0,d_0\)).
   Le pied D de la perpendiculaire abaissée de \(P_0\) sur \(d_0\) (qui peut ne pas être un point de E) détermine sur \(d_0\) deux demi-droites. Par hypothèse, \(d_0\) relie deux points de E et en comprend un troisième. Deux de ces trois points appartiennent à une même droite d’origine D. On les note A et B de sorte que B appartienne au segment DA.
   La droite passant par \(P_0\) et A relie deux points de E : on la note \(d_1\) ; elle ne contient pas B, sinon \(d_1 = d_0\) et \(P_0\) appartiendrait à \(d_0\).
   Les droites \(d_0\) et \(d_1\) se coupent en A et ne sont donc pas parallèles. La perpendiculaire \(P_0D\) ne peut pas être en même temps perpendiculaire à \(d_1\) ; donc le pied de la perpendiculaire abaissée de D à \(d_1\) n’est pas \(P_0\). Par l’inégalité triangulaire, on a \(|P_0d_0| = |P_0 D| > |Dd_1|\).
   Comme B se trouve entre A et D, \(|Dd_1| \le |Bd_1|\), ce qui donne par transitivité l’inégalité \(|P_0d_0| > |Bd_1|\). Comme (B,\(d_1\)) est un élément de F ainsi que (\(P_0,d_0\)), la dernière égalité contredit l’hypothèse que |\(P_0d_0\)| est la distance minimale de l’ensemble F.

   Remarque : cette propriété peut s’exprimer de la façon suivante : « Si un nombre fini de points du plan ne sont pas tous alignés, alors il y a au moins une droite ne passant que par deux d’entre eux ».

   Il existe d’autres démonstrations de ce théorème [8], utilisant par exemple le plan projectif et la notion d’angle minimal (Gallai), ou le plan projectif et la relation d’ordre (Steinberg).

   Notons que ce théorème peut être formulé de façon champêtre : « Dans une forêt dont tous les arbres ne sont pas alignés, il est toujours possible de trouver une droite ne reliant que deux arbres ». Il peut encore être formulé en d’autres termes : « Si E est un ensemble fini de points du plan tel que toute droite passant par deux points de E passe aussi par un troisième point au moins, alors, tous les points sont alignés ».

c) Droite de Wallace (1797)

Soit un triangle ABC et un point P appartenant à son cercle circonscrit c. Les pieds \(A_0, B_0\) et \(C_0\) des perpendiculaires issues de P sur chacun des côtés du triangle ABC sont situés sur une même droite appelée « droite de Wallace ».

La démonstration de cette propriété utilise uniquement le théorème de l’angle inscrit.

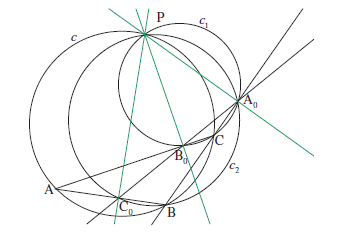
Démontrer que \(A_0, B_0\) et \(C_0\) sont alignés revient à prouver que les droites \(A_0B_0\) et \(A_0C_0\) coïncident, c’est-à-dire, par exemple, que \(\widehat{PA_0B_0}=\widehat{PA_0C_0}\)
Pour démontrer cette égalité, nous allons construire les cercles passant respectivement par les points P, \(A_0, B_0, C\) et par les points P, \(A_0, C_0, B\).
PC est l’hypoténuse de deux triangles rectangles \(PA_0C\) et \(PB_0C\), dont les sommets appartiennent à un cercle \(c_1\).
PB est l’hypoténuse de deux triangles rectangles \(PA_0B\) et \(PC_0B\), dont les sommets appartiennent à un cercle \(c_2\).
Utilisons maintenant le théorème du cercle inscrit dans chacun de ces cercles pour faire apparaître l’égalité.

Dans \(c_1\) : \(\widehat{PA_0B_0}=\widehat{PCB_0}=\widehat{PCA}\) (puisque \(B_0\) est sur AC).
Dans \(c\) : \(\widehat{PCA}=\widehat{PBA}=\widehat{PBC_0}\) (puisque \(C_0\) est sur AB).
Dans \(c_2\) : \(\widehat{PBC_0}=\widehat{PA_0C_0}\)
Par transitivité de l’égalité, nous avons donc bien \(\widehat{PA_0B_0}=\widehat{PA_0C_0}\)

d) Droite d’Euler (1707-1783)

Dans un triangle, l’orthocentre H, le centre de gravité G et le centre O du cercle circonscrit au triangle sont alignés.

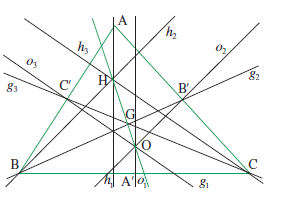
Une façon élégante de démontrer cette propriété consiste à utiliser le fait que l’homothétie de centre G et de rapport −1/2 applique le triangle ABC sur le triangle A’B’C’ et que les hauteurs de ABC sont appliquées sur ses médiatrices. On a donc \(\overrightarrow{GH}=-2\overrightarrow{GO}\) , et les points O, G, H sont forcément alignés.

Il existe d’autres démonstrations de cette propriété, utilisant la relation d’Euler et le fait que G soit le centre de gravité [9].

e) Quelques situations-problèmes

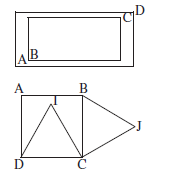
1. On donne un cadre rectangulaire en carton et on demande à quelles conditions les quatre points ABCD sont alignés [10].

2. On donne un carré ABCD et deux triangles équilatéraux DIC et BJC construits sur les côtés du carré, le premier à l’intérieur et le second à l’extérieur. On demande si les points A, I, J sont alignés [11].

Ceci nous montre la variété des exploitations possibles du concept d’alignement.

3. Types de jeux et défis

a) Créer un alignement donné de x points

Jeu du morpion ou oxo ou tic-tac-toe

Ce jeu est sans doute le plus simple sur ce sujet.
Le but du jeu est d’aligner trois des symboles × ou O.

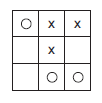
Analyse et stratégie du jeu [12]

Soit X le premier joueur et O son opposant. Le résultat intéressant est le suivant :
si X joue au centre, il est sûr de gagner. En effet,

1. Si O joue ensuite dans la croix, il perd.
   (X joue alors dans une des deux diagonales à côté de O. O est obligé de jouer dans la diagonale opposée pour bloquer la ligne. X joue alors juste en dessous de sa dernière diagonale, il ouvre ainsi deux fronts, auxquels O ne peut répondre en même temps, la partie est gagnée pour X)
2. Si O joue dans la diagonale, X doit jouer dans la même diagonale.
   Le reste dépend du jeu de O. Si O joue sur la même ligne que son premier coup, X est sur la défensive et doit se protéger, sinon, X gagne en créant deux lignes d’attaque.

   

   Selon Martin Gardner, pour avoir une chance égale de gagner que l’on soit premier ou second à jouer, le plateau de jeu doit être de la forme suivante :

N.B. On a là une configuration, solution du premier défi (voir 2.a).

Exploitations pédagogiques et variantes ludiques :

Le principe du jeu est toujours le même : il faut essayer de maximiser le nombre d’alignements possibles.
Citons une variante en jeu individuel : le morpion solitaire, où il faut réaliser un nombre maximum d’alignements de cinq points : on a le droit d’ajouter un point à la configuration si et seulement si cela permet de construire immédiatement un alignement de 5 points (règle supplémentaire éventuelle : si on n’ajoute pas de point pour tracer un segment, on a le droit d’ajouter un point où l’on veut) [13].

Dans son livre « Problèmes et divertissements mathématiques – tome 1 », Martin Gardner propose encore une variante du morpion à quatre dimensions : il faut ici aligner quatre symboles. On peut superposer (à 3 dimensions) les carrés disposés sur une même ligne, colonne ou diagonale.
Voici quelques exemples numérotés : dans un carré (les1), sur une même rangée après superposition (les 2), en diagonale après superposition (les 3) ou (les 4) et en double diagonale après superposition (les 5) ou (les 6).

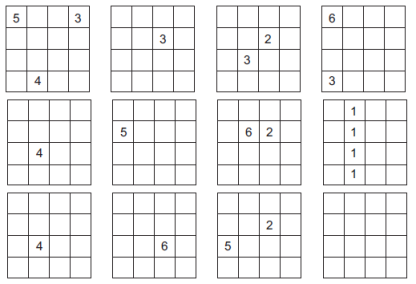
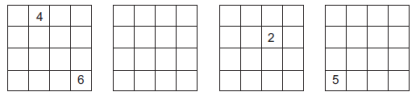
D’autres jeux du commerce exploitent également les alignements : « Puissance 4 », « Egyptos », « Taktik », « Gobblet », « Tetrano », « Puissance 4 à 3 dimensions » (ou « Sogo »).

Jeu de la marelle (ou mérelle)

Ce jeu est assez connu, mais fort peu exploité.
Parmi les nombreuses variantes, nous vous proposons celle-ci :

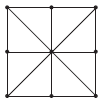
Chacun des deux joueurs dispose de trois pions.
Le but du jeu est d’aligner ses trois pions.
Il y a deux phases de jeu : au début, chaque joueur, à son tour, pose
l’un de ses pions sur une case libre.
Lorsque tous les pions sont placés, chaque joueur peut déplacer l’un
de ses pions sur une case libre voisine.

Analyse et stratégie du jeu [14]

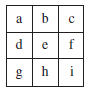
Nommons les neuf cases a-b-c-d-e-f-g-h-i
Appelons les joueurs B (Blanc) et N (Noir)
Notons les déplacements « \(\rightarrow\) ».

Le premier joueur est assuré de gagner en cinq coups. Il y a deux types de cas, les
autres situations étant symétriques :

Be - Na - Bh - Nb (obligé) - Bc (obligé) - Ng (obligé) - Bh \(\rightarrow\) i - N … - Be \(\rightarrow\) f gagne
Be - Nb - Bi - Na (obligé) - Bc (obligé) - Nf (obligé) - Bi \(\rightarrow\) h - N … - Bh \(\rightarrow\) g gagne

En prolongement ou comme variantes, d’autres jeux d’alignements peuvent être
proposés ou analysés : autres « mérelles » pour les plus jeunes, tirées de la revue
« Jeux 1 » ou jeux du commerce tels que « Pente », « Pentago » ou « Yinsh ».
Un autre type d’activité est de compter les alignements possibles.

b) Placer des points pour maximiser les alignements

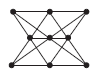
Problème de Newton

Voici une solution de ce problème proposé comme premier défi
(voir 2. a) :

En prolongement, voici un autre problème de plantation intitulé « Savez-vous planter la vigne ? » [15] :
«  Plantez douze ceps de vigne en obtenant exactement dix-huit alignements de trois ceps et un de quatre. »

Problème d’écoliers

L’énoncé de ce problème est celui du deuxième défi (voir 2. a).
Numérotons les différents pions.

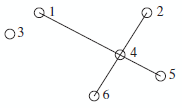
Une première étape est de se rendre compte que l’un des pions (ici o4) est déjà à l’intersection de deux droites o1o5 et o2o6, ce qui donne déjà deux rangées de trois.
Il faut donc déplacer le pion o3 extérieur à cette configuration.
La deuxième étape consiste à essayer de placer le pion entre deux sommets extérieurs consécutifs, ce qui donne trois rangées au lieu de quatre.
La dernière étape à franchir est de placer le pion à l’intersection de deux droites déterminées par des paires de pions consécutifs opposés. Elle n’est pas aisée pour les élèves car elle fait sortir du cadre des cinq pions déjà placés. Selon le dessin initial, il peut y avoir 0, 1 ou 2 réponses (ce qui peut aussi être discuté avec les élèves).

L’intérêt de ce type de problème, comme d’autres problèmes où on demande de compter le nombre d’alignements de n points dans un réseau, est de devoir changer son point de vue, ce qu’on observe, ce qui peut aider à une vision plus mobile dans le plan et dans l’espace.

c) Éviter les alignements

Problème des oeufs
Analysons le troisième problème proposé comme défi (voir 2. a).
Remarquons tout d’abord que pour des enfants très jeunes, on peut supprimer la condition concernant les diagonales, ce qui permet d’avoir un nombre beaucoup plus élevé de solutions.
Face à cette situation, il y a plusieurs niveaux de démarches possibles : l’essai erreur, l’utilisation de la symétrie, la suppression des cases « interdites » par l’énoncé.

On peut donner un prolongement à cet exercice, qui conduira à une réflexion sur le rôle joué par le nombre de cases du carré, avec l’énoncé suivant :
Placer 2n oeufs dans un carré n × n, de sorte qu’il n’y n’ait pas plus de deux oeufs alignés sur chaque ligne, chaque colonne et chaque diagonale. Deux oeufs sont déjà placés aux extrémités d’une diagonale.

On peut alors se poser plusieurs questions : Une solution est-elle toujours possible ? Est-elle toujours symétrique ? Y a-t-il plusieurs solutions superposables ? Le schéma de la solution peut-il être généralisé, par exemple à l’aide d’une démarche de
récurrence ?

Exemples de solutions :
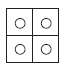
1. - Carré 2 × 2 : une seule solution évidente :

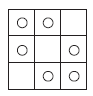
2. - Carré 3 × 3 : une seule solution, symétrique selon deux axes diagonaux :

3.- Carré 4 × 4 : une solution symétrique selon deux axes diagonaux :

Une deuxième solution possédant un centre de symétrie peut aussi être trouvée :

Cette solution offre l’avantage de pouvoir facilement se généraliser aux carrés 2n × 2n.
Elle peut se généraliser aux carrés (2n + 1) × (2n + 1) en plaçant les deux pions en première et dernière ligne sur la colonne centrale (solution possédant un centre de symétrie).

4.- Carré 5 × 5 : deux solutions possédant un centre de symétrie et une solution possédant un axe de symétrie diagonal peuvent être trouvées, la première étant la généralisation qui vient d’être proposée :

Les deux dernières solutions peuvent servir de base pour trouver des solutions dans des carrés plus grands, sans tenir compte des diagonales.

5.- Carré 6 × 6 : une solution symétrique selon deux axes diagonaux et deux axes médians :

Une deuxième solution pour le carré 6 × 6, moins facile à trouver, est symétrique selon deux axes diagonaux :

Elle ne semble pas se généraliser facilement.
Une autre solution est une généralisation de la deuxième solution du cas 4 × 4 :

Remarquons que d’autres solutions peuvent être trouvées si on supprime soit l’occupation initiale des emplacements supérieur gauche et inférieur droit, soit si admet plus de deux places occupées en diagonale.

Carré 3 × 3 : une seule nouvelle solution, sans la contrainte des diagonales (avec d’autres solutions superposables) :

Carré 4 × 4 : plusieurs nouvelles solutions, sans la contrainte des diagonales :
La première peut se trouver à partir de la solution générale pour le carré 3 × 3, et être généralisée à tout carré n × n, ce qui est un exemple de récurrence).

La deuxième peut être trouvée à partir du carré 2 × 2, et permet par la suite de réduire la problème du carré n × n à un problème de carré (n−2) × (n−2) en supprimant les deux premières lignes et les deux premières colonnes, autre cas de récurrence.

Une troisième solution symétrique peut aussi être trouvée partir du carré 2 × 2, et permet par la suite de réduire la problème du carré n × n à un problème de carré (n−2) × (n−2) en supprimant les première et dernière lignes et les première et dernière colonnes (soit le cadre extérieur), autre cas de récurrence.

Voici encore une quatrième solution, possédant un centre de symétrie :

Une cinquième solution, non symétrique mais proche par son procédé de construction de la deuxième solution avec les deux contraintes, peut se généraliser à un carré n × n (placer les pions sur une diagonale, une diagonale parallèle la plus proche et la case opposée à celle-ci. Elle ne respecte pas la contrainte de la diagonale

Il y a encore trois solutions sans élément de symétrie :

Pour le carré 4 × 4, si on ne respecte pas la contrainte du placement de départ, on peut trouver une solution possédant un axe de symétrie :

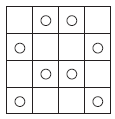
Réseaux de points

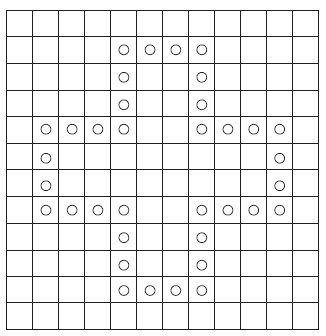
Voici une solution du quatrième problème proposé comme défi (voir 2. a).

Une méthode consiste à analyser à chaque placement les cases possibles ou impossibles pour les pions suivants.

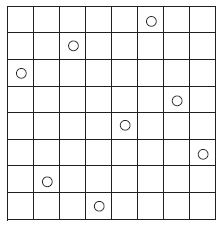
Voici un autre défi très proche [16] :
Sur un réseau 5 × 5 de points à mailles carrée, on peut poser des pions un par un, en respectant les conditions suivantes :

• chaque nouveau pion posé à partir du second doit l’être sur l’une des huit cases voisines d’un pion déjà posé, à condition qu’elle soit libre ;
• l’ensemble des pions posés ne doit jamais contenir un alignement de trois pions (dans une direction quelconque).
  Quel est le nombre maximum de pions qu’il est possible de poser en respectant ces conditions ?

Ce type de problème peut être poursuivi par des problèmes de placement de pièces non en prise directe (c’est-à-dire ne se trouvant pas sur les cases déjà contrôlées par les autres pièces) sur un échiquier : tours (simple), fous (simple), dames (problème proche de celui déjà envisagé, mais sur un carré 8 × 8). La solution proposée plus haut est une solution pour placer 8 tours (il n’y a pas deux pions sur la même ligne ou la même colonne) ou huit fous (il n’y a pas deux pions placés sur une même diagonale) ou huit dames (pour les deux raisons précédentes) sur l’échiquier.

Variante : jeu individuel « Antimorpion »

Ici, des pièces sont déjà placées, et en respectant la même règle (aucun alignement de 4 pions consécutifs de même type), le carré peut être rempli d’une seule façon. Toute erreur de raisonnement conduit à un alignement de quatre pions. Ici, c’est l’idée que l’on ne peut remplir le carré que si on est sûr d’empêcher un alignement qui peut poser problème, mais qui est mathématiquement très intéressante, puisqu’on ne peut remplir que « ce dont on est sûr ».

Exemple [17] :

Une question ouverte qui ne sera pas traitée ici reste posée : quel est le nombre de contraintes minimum pour être sûr de l’unicité de la solution ?

En prolongement, plusieurs jeux de non alignements peuvent être proposés, comme par exemple « Combis et minicombis », jeu analysé dans la revue de l’APMEP « Jeux 5 » (2003), où il faut éviter des « alignements de surfaces ».
Le problème des pions d’Erdös (placer n points dans un carré n × n de telle sorte que les distances entre les points soient toutes différentes) constitue un autre type de prolongement.

4. Pour aller plus loin

Une autre question que l’on pourrait encore se poser est de savoir comment minimiser le nombre de segments de droites pour un réseau de points donné.

Quelques problèmes classiques

1. On donne neuf points disposés en carré. Les relier à l’aide de quatre segments
consécutifs [18].
2. On donne seize points disposés en carré. Les relier à l’aide de six segments consécutifs.

… ou plus originaux
3. On donne vingt-cinq points disposés en carré. Tracer une croix composée de lignes droites reliant douze points de telle façon qu’il y ait cinq points à l’intérieur de la croix, et huit à l’extérieur. La croix doit être symétrique et régulière [19].

Un dernier prolongement possible serait de chercher le plus court chemin permettant d’aller d’un point à un autre moyennant certaines contraintes.

Conclusion

Construire des alignements est sans doute l’une des activités géométriques les plus simples, a donné lieu à plusieurs résultats géométriques intéressants et peut donner lieu à de nombreuses exploitations pédagogiques. C’est aussi une occasion simple d’aborder une démarche d’exploration progressivement structurée par une vision plus systématique dans le plan et dans l’espace, et par là d’aider les élèves à mieux observer une figure géométrique pour en dégager les éléments nécessaires à la résolution d’un problème.

Gageons que cette approche aidera aussi à donner une vision plus attractive des mathématiques !

Bibliographie

COLLECTIF, Jeux 1 : Les jeux et les mathématiques, APMEP, 1982.

AGOSTINI F. et DE CARLO N.A., Les jeux de l’intelligence, France Loisirs, Paris, 1986

BARTHE D., Points à la ligne, Tangente no 99, juillet 2004.

BERLOQUIN P., Points … à la ligne, Jeux et Stratégie no 20, Paris, avril 1983.
BERTE A., Mathématique dynamique, Nathan, Paris, 1993.

BOUTTIER L. et ZAIDENBERG M., Autour du problème de Sylvester, Bulletin de l’APMEP, no 475 p. 243-257, Mars 2008.

CRITON M., Les jeux mathématiques, PUF, Coll. Que sais-je, Paris, 1997.

DUDENEY H., The Canterbury puzzles, Dover, New York, 1958 (Éd. originale : 1907).

DUDENEY H., Amusements in mathematics, Dover, New York, 1958 (Éd. originale : 1917).

GARDNER M., Problèmes et divertissements mathématiques, tome 1, Dunod, Paris, 1964.

GARDNER M., Les casse-tête mathématiques de Sam Loyd, Dunod, Paris, 1970.

GARDNER M., Math’ festival, Belin, Paris, 1981.

LHOTE J.-M., Histoire des jeux de société, Flammarion, 1993.

VAN DELFT, P. et BOTERMANS, J., 1000 casse-tête du monde entier, Éd. Chêne, 1987.

WITTMANN E. Ch., Géométrie élémentaire et réalité, Didier Hatier, Bruxelles, 1998.

Sites internet

http://perso.orange.fr/therese.eveillau/index.htm

http://omegalima.free.fr/strategie/titato.html

http://mathworld.wolfram.com/Orchard-PlantingProblem.html

http://www.apmep.asso.fr/spip.php?article2685

<redacteur|auteur=500>