472
Les décimaux, de l’École au Collège.
par le Groupe de travail
« Activités mathématiques au collège »
Voici le dernier texte du Groupe « Activités mathématiques au collège » de l’APMEP. Nous
avions commencé notre travail par « Fractions au collège » (BV n° 419) et poursuivi par :
« Des fiches pour la classe : Quadrilatères au collège » (BV n° 422). Ont suivi : « Sections
de solides au Collège » (BV n° 427), « Observer… Expliquer… Justifier…
Démontrer… à
partir de la Cinquième » (BV n° 430) et « À propos des aires (1), (2) et (3) » (BV nos 438, 445
et 446).
Ont participé à ce groupe de travail à un moment ou à un autre : Henri Bareil, Catherine
Brunet, François Colmez, Robert Delord, Jacques Germain, Valérie Larose, Maryvonne Le
Berre, Michel Rousselet, Nicole Toussaint.Jean Fromentin, coordonnateur
Les décimaux posent un problème d’enseignement à l’École et au Collège et les
programmes de l’École (2002) et du Collège (2005) insistent très fortement sur la
continuité de ces apprentissages entre les deux niveaux. Signalons tout de suite que
le principal changement concernant les décimaux porte sur la division d’un décimal
par un entier (cf. § Multiplication et division).
Le document d’application du programme du cycle 3 réserve tout un chapitre sur
« Connaissances des fractions et des nombres décimaux » (pages 21 à 24) sans
considérer les opérations sur les décimaux qui se trouvent dans la partie « Calcul ».
Il est un outil essentiel pour le professeur de mathématiques de Collège. Notons que,
dans les précédents programmes du Collège, certaines compétences qui étaient
censées être acquises à l’entrée en sixième ou seulement évoquées dans la colonne
des commentaires, sont maintenant explicitées dans la colonne « Compétences ».
Citons, à titre d’exemple, la compétence suivante : « Encadrer un nombre, intercaler
un nombre entre deux autres ».
Les objectifs conceptuels sur les décimaux dont il était déjà fait état dans la brochure
de l’APMEP n° 61 de février 1986 : « Aides pédagogiques pour le cycle moyen –
Nombres décimaux » sont, bien sûr, toujours d’actualité :
se rendre compte de l’insuffisance des entiers naturels pour résoudre certains
problèmes ;
créer de nouveaux nombres pour résoudre des problèmes qui n’avaient pas de
solution dans les entiers ;
prolonger aux nouveaux nombres l’ordre qu’on avait sur les entiers ;
concevoir qu’entre deux nouveaux nombres, on peut toujours en intercaler un
autre ;
prolonger aux nouveaux nombres les quatre opérations ;
utiliser les nouveaux nombres dans des situations d’approximation.
Ce sont ces objectifs qui doivent guider notre enseignement et c’est ce que nous avons essayé de faire au travers des activités que nous vous proposons ci-après.
Il ne s’agit pas, dans ces activités, de refaire en classe de sixième un apprentissage
complet des décimaux, mais de proposer des situations où les décimaux prennent tout
leur sens pour permettre aux élèves d’entretenir, d’enrichir ou de corriger les
connaissances élaborées antérieurement.
Quelques constats
Les évaluations à l’entrée en Sixième ont permis aux enseignants de prendre
conscience que la principale erreur faite par les élèves est le traitement séparé des
parties entières et décimales dans l’écriture à virgule. Cette erreur se rencontre dans
plusieurs situations :
Dans les additions ou soustractions en ligne de deux décimaux :
30,3 + 15,8 = 45,11 ; 21,15 + 7,6 = 28,21 ou 39,12 − 6,4 = 33,8.
Dans les multiplications par 10, 100 ou 1 000, on observe une constance dans
l’erreur qui est donc bien liée à une mauvaise conception du décimal. Un même
élève opérera sur la partie entière ou sur la partie décimale, voire sur les deux !
Élève A : 35,2 × 10 = 35,20 ou 23,56 × 100 = 23,5600.
Élève B : 35,2 × 10 = 350,2 ou 23,56 × 100 = 2300,56.
Élève C : 35,2 × 10 = 350,20 ou 23,56 × 100 = 2300,5600.
Dans le rangement des décimaux, ce traitement séparé des parties entière et
décimale se manifeste de la façon suivante bien connue : 3,5 < 3,24 < 3,123. La
partie entière étant la même, les parties décimales sont lues comme des entiers.
– En quatrième ou en troisième, il arrive encore de trouver : $2,4^{2} = 4,16$.
Quelles réponses ?
La lecture avec sens est fondamentale
L’usage des expressions « complexes » (3 m 25 cm ; 15 € 35 centimes) et des
écritures décimales qui en découlent (3,25 m ; 15,35 €) peut induire en effet la
conception erronée (deux entiers séparés par une virgule) du nombre décimal et donc
un traitement séparé des parties entière et décimale. Il ne faut pourtant pas négliger
les mesures de grandeurs. À l’exception des durées, elles sont l’occasion, par
l’intermédiaire des conversions, de calculer sur les décimaux, ces calculs donnant du
sens à ces derniers.
C’est en tant que valeurs approchées de rationnels ou de réels que les décimaux ont
leur utilité et prennent vraiment leur sens. À l’occasion d’un calcul qui donne par
exemple comme résultat 3 214 m, il est important que l’élève se représente cette
valeur en mettant en évidence le chiffre significatif par choix de l’unité ad hoc, par
exemple 3 214 m = 3,214 km c’est-à-dire 3 km et quelque. Plus l’unité est petite, plus
la mesure est grande. De la même façon, plus l’unité est grande, plus la mesure est
petite, ce qui est plus difficile pour les élèves car cela nécessite de mettre en œuvre
le concept en cours d’élaboration. Une mesure de grandeur inférieure à 1, c’est
nouveau !
À l’École, les décimaux ont été introduits à partir des fractions décimales, la notion
de fraction ayant été abordée le plus souvent sur des partages simples. Les derniers programmes de l’École et du Collège insistent aussi sur « Parler, lire et écrire en
mathématiques » [1]. Ainsi, pour construire peu à peu une bonne représentation des
décimaux, il est important de dire, de lire en « compréhension » les fractions
décimales ou les nombres décimaux. Par exemple 0,4 et 4/10 sont deux notations du
même nombre qu’on devrait lire « quatre dixièmes » et non pas « zéro virgule quatre
» ou « quatre sur dix ». Le nombre ayant pour écriture décimale : « 3,45 » peut se
lire « 3 unités et 45 centièmes » ou encore « 3 unités 4 dixièmes et 5 centièmes ». Il
peut aussi être lu « 345 centièmes » et peut être écrit 3 + 45/100 ou 3 + 4/10 + 5/100
ou encore 345/100. La lecture « trois virgule quarante-cinq », bien pratique, pourra
être utilisée seulement lorsque le concept de décimal sera bien installé, quitte à faire
le lien, quand cela est nécessaire, avec la lecture « Trois unités plus quarante-cinq
centièmes ». Les variétés d’écritures (décimales et fractionnaires) et les lectures
associées sont primordiales pour une bonne appropriation du nombre décimal.
La division par 0,1 et 0,01 est supprimée dans le programme actuel de sixième. Elle
relevait plus du mécanisme que de la compréhension [2]. En revanche, la
multiplication et la division par 10 et 100, la multiplication par 0,1 et 0,01 participent
à la construction du sens sur les décimaux.
Multiplication et division
Comme dans les programmes précédents, la multiplication de deux entiers et celle
d’un décimal par un entier sont des compétences de fin de cycle 3. La multiplication
de deux décimaux relevait déjà du programme de sixième. Il y a en effet un saut
conceptuel à franchir de la part des élèves à propos de cette dernière compétence. En
ce qui concerne la division, seule la division euclidienne reste au programme du
cycle 3, avec l’acquisition du sens du quotient et du reste ainsi que la pratique du
calcul posé. Mais, pour être tout à fait clair à ce sujet, citons les commentaires du
document d’application du programme du cycle 3 :
« Le calcul de divisions (quotient entier et reste) doit être limité à des cas
“ raisonnables ” : dividende ayant au plus 4 chiffres, avec pose effective des
soustractions intermédiaires et possibilité de poser des produits partiels annexes
pour déterminer certains chiffres du quotient. L’algorithme de la division sera repris
dans le programme de sixième et prolongé au cas du quotient décimal.
Le calcul d’un quotient décimal issu de la division de deux entiers ou d’un décimal
par un entier n’est donc pas une compétence exigible au cycle 3. Mais des situations
où les élèves sont conduits à chercher ce type de résultat par des procédures
personnelles doivent être proposées. Par exemple, s’il s’agit de partager
équitablement 203 euros entre 5 personnes, les procédures suivantes peuvent être
utilisées :
convertir les 203 euros en 20 300 centimes, puis effectuer la division ;
donner 40 euros à chacun, puis convertir les 3 euros restants en 300 centimes
pour terminer le partage ;
“ poser la division de 203 par 5 ”, puis convertir le reste (3 unités) en 30
dixièmes pour poursuivre le calcul.
Dans tous les cas, on reste au niveau d’un calcul réfléchi explicite, sans viser la mise
en place d’un automatisme. La calculatrice peut également être utilisée lorsque, par
exemple, le calcul de la division de 203 par 5 a été reconnu comme pertinent,
l’attention des élèves devant être attirée sur l’interprétation du résultat affiché,
notamment sur les chiffres significatifs de la partie décimale. »
Vous trouverez à la fin de cet article, un texte concernant l’apprentissage de la
division : « La technique de la division de l’École élémentaire au Collège ». Ce
texte n’est pas une activité, mais il décrit de façon précise l’évolution de la technique
opératoire de la division en liaison avec le sens de cette opération. Rappelons que
c’est dans le cadre de la résolution de problèmes que cette technique est mise en
place. Ce texte sera très utile pour assurer la continuité des apprentissages de l’École
au Collège.
Activités sur les décimaux [3]
Voici, décrites les unes après les autres, les activités proposées sur les décimaux. Ces
activités concernent à la fois l’École et le Collège. À l’École, elles peuvent être
utilisées comme activités de construction, de structuration ou de consolidation (pour
reprendre les différents niveaux d’études d’une notion présentés dans les éléments
d’aide à la programmation du document d’application des programmes du cycle 3),
suivant l’année ou le niveau des élèves. Au Collège, elles peuvent être utilisées
comme activités de structuration ou de consolidation suivant les difficultés observées
chez les élèves.
Rectangles de même périmètre – Rectangles de même aire
La première activité « Rectangles de même périmètre » est plutôt destinée aux
élèves de l’École. La notion de périmètre peut être abordée assez tôt et les mesures
de longueur peuvent donc servir de support aux nombres décimaux. Les
changements successifs de cadre (géométrique, numérique, graphique), avec une
interaction permanente entre les trois domaines, facilitent la découverte de ces
nouveaux nombres et assurent leur « existence ».
La deuxième activité « Rectangles de même aire », construite sur le même principe
que la précédente, en est un prolongement. Un peu plus complexe, du fait de
l’utilisation de la notion d’aire et du non-alignement des points du graphique, elle est
toutefois facilitée par l’activité précédente sur les périmètres. La recherche du carré
qui a une aire de $12 cm^{2}$ est, bien sûr, le temps fort de ce travail. Les élèves pourront
approcher, à l’aide de la calculatrice, la mesure du côté du carré autant qu’ils le
souhaiteront (en dépassant la plus petite unité de longueur qu’ils connaissent : le
millimètre), ce qui est primordial dans l’acquisition du concept de nombre décimal. Cette activité, destinée aussi aux élèves de l’École, trouve également sa place en
classe de sixième pour, justement, entretenir, améliorer ou corriger les conceptions
que les élèves ont sur les décimaux, comme nous le disions plus haut. Il va de soi que
l’utilisation de la touche « racine carrée » ruinerait toute la richesse de cette activité.
Une autre approche possible, à l’occasion de cette activité, est de faire travailler les
élèves sur des zones graphiques : colorier en rouge les points qui représentent des
rectangles dont l’aire est plus petite que $12 cm^{2}$ ; colorier en vert les points qui
représentent des rectangles dont l’aire est plus grande que $12 cm^{2}$ ; apparaîtra alors
une zone « frontière » où les élèves pourront situer à peu près le point qui
représentera le carré d’aire $12 cm^{2}$.
Pour ces deux activités, ainsi que pour les suivantes, le rétroprojecteur permettra une
meilleure communication avec les élèves.
En y regardant de plus près !!
Comme les précédentes, cette activité trouve sa place à la fois en cycle 3 et en classe
de sixième. On reste dans le domaine de la mesure ; mais la seconde étant utilisée
comme unité de temps, les élèves ne peuvent pas choisir de sous-unités pour se
ramener à des entiers. Nous ne pensons pas que la notion de vitesse, en jeu ici, soit
un obstacle pour les élèves.
Cette activité a plusieurs objectifs :
Travailler sur les écritures décimales et fractionnaires et sur l’expression orale de
ces écritures ;
Se rendre compte de la nécessité, pour pouvoir comparer, d’utiliser des
graduations plus fines : le dixième, le centième ;
Construire une bonne représentation mentale, à l’aide des zooms successifs, de
l’intercalation toujours possible d’un décimal entre deux décimaux.
Toujours plus près !!
De la droite au plan, la route rectiligne assure le lien avec l’activité précédente. La
notion d’échelle mise en jeu ici ne nous semble pas être un obstacle pour les élèves
puisqu’il s’agit de rester dans les représentations mentales : 1 cm représentant 1 km.
L’objectif principal est la comparaison de décimaux. Contrairement à l’activité
précédente, il ne s’agit pas de placer précisément les points sur la carte, ce qui serait
d’ailleurs impossible, mais de comparer des décimaux en s’aidant de la situation
géométrique proposée. L’interaction entre les cadres géométrique et numérique, par
l’intermédiaire de la mesure, facilite la compréhension du problème et la
familiarisation avec les décimaux.
La machine infernale
La multiplication et la division par 10 sont bien sûr à la base de notre système de
numération décimale. La pratique de ces opérateurs ne peut que faciliter
l’appropriation du concept de nombre décimal. Les « passages » de chiffres de la
partie entière vers la partie décimale et réciproquement ne peuvent qu’aller à
l’encontre de la mauvaise représentation du décimal signalée précédemment : « deux
nombres entiers séparés par une virgule ». De plus, cette activité très ludique par les défis à relever ne nécessite pas, contrairement à ce que le début du texte pourrait
laisser entendre, l’utilisation de la calculatrice.
Au contraire, les multiplications et
divisions par 10, par 100, par 1000 font partie du domaine du calcul mental
automatisé signalé dans les programmes de l’école primaire.
Pas touche
Cette fiche n’est pas prévue pour un travail totalement autonome des élèves. En
particulier, la première partie nécessite un travail collectif.
Ici, la calculatrice est utile. Mais il est évident qu’elle sert essentiellement à valider
la série de calculs que l’élève aura trouvée. La recherche se fait obligatoirement
mentalement ; c’est la pensée qui précède l’action. Comme dans l’activité
précédente, l’élève doit agir sur les fondements même de notre système de
numération décimal et c’est cela qui est très formateur.
Dans la troisième partie, les élèves ne sont pas obligés d’utiliser des produits avec les
seules puissances de 10. Par exemple, ils peuvent obtenir 300 avec 50 × 6.
La multiplication des décimaux
Les documents sur la multiplication des décimaux sont organisés en deux parties.
Une première partie concerne les produits de puissances de 10. Il ne s’agit pas ici
d’utiliser la notation sur les puissances de 10 ; il s’agit au contraire d’expliquer aux
élèves quels sont ces nombres qu’on appelle « puissances de 10 », de travailler sur
leurs deux écritures (fractionnaire et décimale) et sur leur dénomination.
L’acquisition du sens des nombres décimaux et des capacités à opérer sur les
décimaux passe en effet par la faculté de dire, d’écrire ces nombres et de passer d’une
écriture à l’autre. C’est pourquoi les trois fiches de travail de cette première partie
font lire, écrire et opérer les élèves sur ce que nous appelons les puissances de 10
sous les trois formes énoncées précédemment. La compréhension et la maîtrise du
produit de deux nombres décimaux passent par la maîtrise du produit des puissances
de 10. Il est bien évident que ces puissances de 10 (unité, dizaines, centaines, …
dixièmes, centièmes, …) doivent avoir du sens pour les élèves. Pour cela, une activité
telle que « En y regardant de plus près » peut y aider.
La deuxième partie comporte trois fiches. Les deux premières s’adressent plutôt au
professeur. Ce dernier peut les utiliser devant les élèves, à l’aide du rétroprojecteur,
pour leur expliquer la méthode « per gélosia » décrite ici. Cette méthode est
particulièrement intéressante dans une activité de soutien. Elle ne handicape pas les
élèves qui ont des difficultés dans la connaissance des tables. Contrairement à la
technique habituelle de la multiplication, les produits partiels étant tous écrits
complètement, il est facile de repérer les erreurs de tables. La disposition utilisée
permet de gérer facilement les différentes unités (unités, dizaines, centaines, …
dixièmes, centièmes, …).
La première fiche concerne les nombres entiers, la
deuxième fiche les nombres décimaux. Dans cette deuxième fiche, le professeur a le
choix entre deux méthodes proposées. Une troisième méthode peut consister à faire
évoluer les élèves de la première vers la deuxième en veillant toujours à ce qu’ils
gardent le sens de ce qu’ils font. La troisième fiche propose quelques exercices en
complément de l’une et de l’autre des deux fiches précédentes.
Conclusion
La lecture seule du texte officiel des programmes du cycle 3 de l’École primaire
parus au BO hors série n° 1 du 14 février 2002 n’est pas suffisante pour assurer une
bonne liaison entre l’École et le collège. Aussi, nous invitons le lecteur à consulter
les deux documents suivants qui accompagnent ces programmes et qui nous
paraissent essentiels. Ces deux documents édités par le CNDP ont été en principe
adressés à tous les collèges. Ils devraient figurer dans chaque CDI.
Le document d’application (cycle 3), présenté en deux colonnes, donne en regard
de chaque compétence des indications d’ordre pédagogique, des précisions de
niveaux d’approfondissements et assure le lien avec le cycle 2 en amont et avec la
classe de sixième en aval. Vous trouverez en particulier dans l’introduction de ce
document deux thèmes étroitement liés à l’objet de cet article, « La question du
calcul aujourd’hui » et « Parler, lire et écrire en mathématiques ». La dernière partie
de ce document propose des éléments d’aide à la programmation des apprentissages
sur les trois années du cycle 3.
Cette partie intéresse particulièrement le professeur
de mathématiques de sixième car cette programmation inclut, en perspective, la
classe de sixième. Ainsi, pour chaque compétence, un tableau indique à quel moment
chacun des trois types d’activités : approche/préparation, construction/structuration
et consolidation/utilisation peut être proposé aux élèves. On peut y observer que la
plupart des compétences sur les décimaux sont encore en phase de construction et de
structuration en sixième.
Les documents d’accompagnement regroupés dans une même brochure traitent
différents thèmes sur l’ensemble des deux cycles de l’École Élémentaire. En liaison
avec cet article, vous pourrez lire plus particulièrement « Le Calcul mental à l’École
élémentaire », « Le calcul posé à l’École élémentaire », « Utiliser les calculatrices
en classe », « Grandeurs et mesure à l’École élémentaire » et « Articulation École –
Collège ».
La technique de la division de l’école élémentaire au collège
La division euclidienne
La division euclidienne (dont on ne prononce pas forcément le nom à l’École) est
introduite au cycle 3 (toujours en référence à la résolution de problèmes) : Le calcul
de divisions … cf. pages 26/27 du document d’application des programmes du
cycle 3.
La présentation suivante de la technique opératoire est inspirée d’une brochure
« Nombres décimaux », liaison École/Collège de l’IREM de Paris 7. Elle s’appuie
sur l’encadrement du dividende par deux multiples consécutifs du diviseur,
encadrement lié au placement d’une fraction$\frac{a}{b}$ sur une droite graduée. Il s’agit donc de trouver l’entier q tel que q < a/b < q + 1, ce qui revient à : b × q < a < b × (q + 1) ;
q est alors le quotient entier à une unité près par défaut, et q + 1 le quotient entier à
une unité près par excès. Le reste de la division : r = a - b × q est plus petit que b.
Exemple : $436 : 17 = \frac{436}{17}$.
Un petit travail sur les ordres de grandeur indique que le
quotient est compris entre 10 et 100 (donc un nombre à deux chiffres) et de l’ordre
de 20 en écrivant d’abord les multiples de 17 par les dizaines entières successives :
17 × 10 = 170
17 × 20 = 340
17 × 30 = 510
On s’arrête car le multiple rencontré est plus grand que le dividende. Ainsi, le
quotient entier est compris entre 20 et 30.
436 − (17 × 20) = 436 – 340 = 96 et 96 < 17 x 10
On prend alors les multiples successifs de 17 jusqu’à en rencontrer un plus grand que
96 :
17 × 1 = 17
17 × 2 = 34
17 × 3 = 51
17 × 4 = 68
17 × 5 = 85
17 × 6 = 102
96 = 85 + 11 = (17 × 5) + 11 et 11 < 17
On peut profiter de la phase précédente pour rappeler que « réciter la table des 17 »
consiste à « compter de 17 en 17 à partir de 0 ».
On a donc :
436 = 340 + 85 + 11 = (17 × 20) + (17 × 5) + 11 = 17 × 25 + 11.
Dans un premier temps, on adopte la disposition suivante :

Cette présentation va s’alléger, plus ou moins vite selon les élèves, pour aboutir à une
disposition telle que :
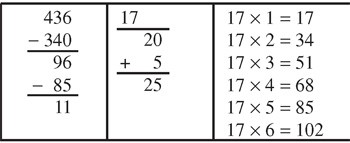
Puis, à celle, plus connue, tout en maintenant les soustractions écrites et
éventuellement, à la disposition habituelle qu’il n’est même pas obligatoire que tous
les élèves atteignent. En effet, il est préférable d’entretenir le sens de la division au
travers de la technique opératoire enseignée.
Quotients décimaux approchés ou exacts (« Poursuite » de la
division d’entiers)
Les élèves arrivant en sixième auront rencontré des quotients décimaux dans des
résolutions de problèmes, mais n’auront pas, en principe, la maîtrise de la technique
opératoire correspondante.
Reprenons l’exemple précédent, avec la première disposition proposée.
Les élèves savent que $11= \frac {110}{10}$ ; donc, en prenant le $\frac {1}{10}$ comme unité, cela revient
à situer 110 parmi les multiples de 17, ou encore 11 parmi les produits 17 × 0,1 ;
17 × 0,2 ; 17 × 0,3 ; etc.
On passera ensuite aux centièmes, puis aux millièmes, et ainsi de suite, ce qui permet
d’étendre la technique opératoire à la recherche de quotients décimaux.
<imd10524|center>
436 = (17 × 25,647) + 0,001
On peut aussi ne pas mettre les virgules dans les opérations successives en changeant
à chaque ligne d’unité de référence, ce qui relève de l’habituel « j’abaisse un zéro
après avoir mis une virgule au quotient dès que je n’ai plus de chiffres à abaisser
dans le dividende », mais il faut bien avouer que cela n’a pas beaucoup de sens pour
un bon nombre d’élèves.
Quotients d’un décimal par un entier
La technique précédente s’adapte immédiatement si on veut s’arrêter au quotient
entier :

436,207 = 17 × 25 + 11,207
Pour trouver des quotients décimaux, on reprend, là aussi, toujours la même
disposition, en passant comme précédemment aux dixièmes, aux centièmes, …, mais
en tenant compte cette fois des dixièmes, des centièmes qui figurent dans le
dividende, c’est-à-dire en « abaissant » les chiffres successifs de la partie décimale
du dividende :

436,207 = 17 × 25,659 + 0,004
25,659 est une valeur approchée au millième du quotient ; on peut obtenir des valeurs
approchées plus précises en poursuivant le processus, c’est-à-dire en « ajoutant » des
zéros à la partie décimale du dividende.
Quotients d’un décimal par un décimal
Prévu maintenant au niveau Cinquième, ce travail est commenté par la phrase : « à
conduire en relation avec les égalités d’écritures fractionnaires ».
Ainsi : $436,207:17,08 =\frac{436,207}{17,08}= \frac{43620,7}{1708}= 43620,7 : 1708$
Chercher les quotients décimaux de 436,207 par 17,08 revient donc à chercher les
quotients décimaux de 43 620,7 par 1 708, ce qui aura été fait au niveau Sixième et
ne devrait nécessiter qu’un entretien, avec cependant la remarque que si le
quotient est le même, le reste ne l’est pas :
436,207 = 17,08 × 25,53 + 0,1546
43 620,7 = 1 708 × 25,53 + 15,46.