498
Mathématiques actuelles et enseignement des mathématiques : quelles synergies ?
Mathématiques actuelles et enseignement des mathématiques : quelles synergies ? [1]
par Michèle Artigue [2]
1. Introduction
Les journées de l’APMEP 2011, intitulées « Mathématiques en Marche », nous ont
donné à voir les mathématiques comme une science vivante, dynamique,
indispensable aux avancées technologiques, indispensables aussi pour répondre aux
grands défis auxquels fait face l’humanité, et des mathématiques interagissant pour
cela avec un nombre croissant de domaines. À un moment où l’on peut légitimement
s’inquiéter pour l’avenir de l’enseignement des mathématiques, tant semblent
s’accumuler les obstacles et les contraintes, se détériorer les conditions d’exercice du
métier d’enseignant et celles de la formation des maîtres, initiale comme continue,
on peut envier ce dynamisme des mathématiques et vouloir y puiser des sources
d’inspiration, une stimulation. C’est ce qui m’a amenée à choisir ce thème des
synergies possibles entre mathématiques et enseignement des mathématiques pour
ma conférence à ces journées. Penser ces synergies ne peut se faire sans considérer
le maillon clef qu’est la formation des enseignants, car il semble bien illusoire de
vouloir les faire vivre dans la réalité des classes si elles sont inexistantes dans la
formation initiale et continue de ces derniers. Ceci m’a conduite à accorder une place
importante dans mon exposé au projet Felix Klein, un projet lancé récemment par
l’ICMI (Commission internationale de l’enseignement mathématique) dans lequel
je suis personnellement impliquée.
Quittant le domaine de la formation des
enseignants, je suis ensuite revenue à l’enseignement lui-même et j’ai interrogé dans
cette perspective les évolutions curriculaires récentes, en me posant les questions
suivantes : Ont-elles cherché à établir des ponts entre les mathématiques actuelles et
l’enseignement ? Ont-elles réussi ? Quelles leçons pouvons-nous en tirer pour penser
plus efficacement les synergies entre les mathématiques qui se font et les
mathématiques qui s’enseignent, pour faire que l’image que se font nos élèves des
mathématiques soit celle d’une science vivante mais aussi celle d’une science qui
leur semble accessible ?
2. La coupure entre mathématiques qui se font et mathématiques enseignées : une question récurrente
Quand on parle d’évolution des mathématiques, on met souvent en avant les
caractéristiques suivantes :
- l’explosion dans la production de connaissances, et celle associée des
publications ; - les changements d’équilibre dans l’édifice global avec notamment la place
prise par les probabilités, un domaine encore à la frontière des mathématiques
au début du 20ème siècle et qui féconde aujourd’hui tous les domaines des
mathématiques ; - l’importance croissante des connexions, internes et externes, l’investissement
de nouveaux champs et les nouvelles sources d’inspiration que les
mathématiciens y trouvent ; - le rôle clef que jouent les mathématiques dans les avancées technologiques ;
- le rôle qu’elles peuvent et doivent jouer pour éclairer les grands défis
auxquels l’humanité fait face et aider à y faire face ; ainsi l’année 2013 sera-t-
elle l’année des mathématiques de la planète Terre ; - mais aussi l’évolution des pratiques mathématiques, la part croissante que
prennent dans ces pratiques, grâce à l’évolution technologique, démarches
expérimentales et simulations.
Et il est aussi fréquent d’entendre dire que, comparativement, l’enseignement ne
donne aujourd’hui à voir et à pratiquer aux élèves que des mathématiques vieilles de
plusieurs siècles, sinon de millénaires, bref une science morte et ce, avec des
pratiques elles aussi inchangées. Les liens entre les mathématiques qui se font et les
mathématiques qui s’enseignent seraient coupés, et ceci aurait des conséquences
lourdes sur l’engagement des élèves, leur réussite, leurs choix d’orientation, …
Quel est le degré de véracité d’une telle affirmation ? J’y reviendrai ultérieurement.
Chacun a son mot à dire sur l’enseignement et ce n’est pas parce que des déclarations
viennent de brillants esprits, voire de brillants mathématiciens, que nous ne devons
pas les soumettre à l’étude et à la critique. Mais, je voudrais en fait tout d’abord
rappeler qu’il s’agit là d’une affirmation qui n’est en rien nouvelle. Elle a fondé les
discours soutenant la réforme des mathématiques modernes il y a une cinquantaine
d’années mais bien avant, la trop grande distance avec la science qui se fait, c’était
déjà ce que reprochait à l’enseignement le grand mathématicien Felix Klein au début
du 20ème siècle. C’est ce qui le poussa à s’engager dans le mouvement de réforme
en Allemagne connu sous le nom de réforme Meran, et à organiser, pour aider à
réduire cette distance, une série de conférences pour les enseignants de gymnasium
qui allait donner lieu au célèbre ouvrage Elementarmathematik vom höheren
Standpunkte aus plus connu dans sa version anglaise Elementary mathematics from
an advanced standpoint (Klein, 1924, 1932).
Comme il l’explique dans la préface du premier tome, Felix Klein entend en fait
lutter contre ce qu’il perçoit comme une double discontinuité entre enseignement, secondaire et enseignement supérieur, entre la science enseignée et la science en
marche. Il la décrit ainsi : une première rupture se produit lorsque les étudiants,
sortant de l’enseignement secondaire, entrent en contact avec des mathématiques
complètement nouvelles à l’université, une seconde lorsque, formés par l’université,
ils sont censés mettre leurs connaissances universitaires au service de l’enseignement
secondaire. Et pour lutter contre cette double discontinuité, il se propose de :
« mettre à la disposition de l’enseignant, mais aussi de l’étudiant avancé, selon
les points de vue de la science moderne mais d’une manière aussi simple,
stimulante et convaincante que possible, à la fois le contenu et les fondements des
sujets enseignés, en prêtant l’attention requise aux méthodes actuelles
d’enseignement » (p. III, notre traduction)
Il s’agit aussi, ce faisant, de promouvoir les réformes nécessaires. À cette époque, la
place à accorder dans l’enseignement à la notion de fonction est un point important
de débat et Felix Klein prend clairement parti :
« Nous, qui sommes appelés les réformateurs, voudrions mettre le concept de
fonction au centre de l’enseignement parce que, de tous les concepts
mathématiques des deux derniers siècles, c’est celui qui joue le rôle majeur
partout où la pensée mathématique est utilisée. Nous voudrions l’introduire dans
l’enseignement aussi tôt que possible, avec un usage constant de la méthode
graphique, la représentation des relations fonctionnelles dans le système de
coordonnées x y, qui est utilisée aujourd’hui dans toutes les applications pratiques
des mathématiques (ibidem, p. IV, notre traduction)
Il reconnaît certes la nécessité d’un certain décalage entre les avancées les plus
récentes de la science et l’enseignement mais trouve la situation de l’époque en ce
qui concerne les fonctions tout à fait inacceptable car pour l’essentiel,
l’enseignement ignore selon lui tous les développements intervenus depuis l’époque
d’Euler, et il ajoute :
« Nous désirons simplement que la notion générale de fonction, selon l’une ou
l’autre des interprétations d’Euler imprègne comme un ferment l’enseignement
entier des mathématiques au lycée. Elle ne doit pas, bien sûr être introduite au
moyen de définitions abstraites mais transmise aux élèves comme une possession
vivante, au moyen d’exemples élémentaires, comme l’on en trouve de multiples
exemples chez Euler » (ibidem, p. 205)
Comme on le voit, le discours mêle considérations mathématiques et didactiques. Sur
le plan didactique, il est porté par une vision « génétique » de l’apprentissage dont
on connaît aujourd’hui les limites mais qui est très partagée à l’époque (Schubring,
2011). Selon cette vision, l’enseignement, pour être efficace, ne doit pas présenter la
science aboutie mais faire suivre à l’élève les étapes de l’évolution historique. Mais,
même si l’on ne partage pas cette vision de l’apprentissage, on ne peut qu’être
d’accord avec la position de Felix Klein qui considère qu’une réflexion sur les
synergies nécessaires entre évolution des mathématiques et évolution de
l’enseignement, ne peut se faire uniquement à travers une réflexion mathématique sur les contenus d’enseignement. Elle doit penser les transpositions didactiques, les
stratégies qui peuvent rendre ces synergies possibles dans un système donné. Si Felix
Klein a une vision de l’enseignement et l’exprime, il laisse en revanche aux
enseignants la responsabilité de penser le détail de ces transpositions, d’imaginer les
stratégies précises, de construire les ressources nécessaires pour l’enseignement.
Cela relève de leur expertise. Il a d’ailleurs affaire à une audience de professeurs
experts. Il voit ainsi son livre :
« seulement comme un stimulus mental, non comme un manuel détaillé. »
(ibidem, p. IV, notre traduction).
Il insiste enfin sur les connexions entre domaines mathématiques, voyant également
dans ces dernières le moyen pour les enseignants de faire sens utilement de toutes ces
évolutions :
« Ma tâche sera toujours de montrer les connexions mutuelles entre les problèmes
des divers champs. J’espère ainsi vous rendre plus facile la capacité d’extraire de
la grande base des connaissances existantes une inspiration pour votre
enseignement. » (ibidem, p. IV, notre traduction).
La situation aujourd’hui n’est pas celle du début du 20ème siècle mais penser les
rapports entre évolution des mathématiques et évolution de l’enseignement est une
question toujours difficile, et qui se pose dans des termes sans cesse renouvelés. Elle
est renouvelée par l’évolution des sciences mathématiques mais aussi par l’évolution
des sociétés et des attentes qui s’y expriment vis-à-vis de l’enseignement des
mathématiques, comme par celle des moyens matériels et humains qui sont mis au
service de cet enseignement.
S’agissant de l’évolution des sciences mathématiques, l’évolution est multiforme, et
comme le soulignait Laszlo Lovász, président de l’Union mathématique
internationale (IMU), dans une conférence à Lisbonne consacrée au futur de
l’enseignement des mathématiques en Europe (Lovász, 2007), même au sein de la
communauté mathématique, chacun ne connaît sérieusement aujourd’hui qu’une
portion très limitée du paysage global. Rendre, même en restant essentiellement au
niveau des idées, sans viser l’opérationnalité technique, les mathématiques qui se
sont développées au cours du 20ème siècle accessibles aux enseignants et source
d’inspiration pour eux, comme avait voulu le faire Felix Klein en son temps est un
réel défi. C’est un défi que nous essayons de relever au sein de l’ICMI, dans une
collaboration étroite entre mathématiciens et didacticiens, à travers le projet Felix
Klein.
3. Le projet Felix Klein
Il s’agit en effet dans ce projet de rendre des développements mathématiques
importants du 20ème siècle accessibles aux enseignants et source d’inspiration pour
leur enseignement. Des développements et non les développements car tous ne sont
sans doute pas accessibles avec la culture mathématique d’un enseignant de lycée,
même intéressé aux mathématiques, tous ne peuvent pas nécessairement être source d’inspiration pour l’enseignement secondaire. Il s’agit de penser ces développements
en termes de contenus comme de pratiques, sans oublier leurs effets sur les
mathématiques fondamentales de l’École. Il s’agit aussi d’organiser la collaboration
nécessaire entre communautés pour mener à bien un tel projet, et d’utiliser les
technologies actuellement disponibles pour organiser le travail, penser les ressources
utiles et leur dissémination.
Pour piloter ce projet, l’ICMI et l’IMU ont constitué un comité de pilotage composé
de huit membres, mathématiciens et/ou didacticiens, dirigé par le président de
l’ICMI, Bill Barton, qui a lui-même une longue expérience d’enseignant du
secondaire. L’ambition du groupe est de produire un livre de 300 pages environ pour
les professeurs du secondaire et plus particulièrement ceux enseignant au niveau
lycée. Ce livre, qu’il est prévu de publier simultanément en plusieurs langues, doit
être stimulant, combiner des chapitres centrés sur des domaines mathématiques,
comme l’étaient ceux des ouvrages de Felix Klein, et des chapitres « transversaux »
mettant en évidence l’importance des connections internes et externes en
mathématiques, ainsi que les façons de travailler des mathématiciens. Comme
souligné plus haut, Felix Klein déjà se donnait l’ambition de montrer les connexions
entre domaines mathématiques. Au cours du 20ème siècle ces connections se sont
multipliées mais se sont aussi développées les connexions avec de nombreux
domaines hors des mathématiques, bien au-delà des relations traditionnelles entre
mathématiques et physique. C’est pourquoi, tout en étant particulièrement attentifs à
ces questions tout au long du livre, il nous a semblé nécessaire de réserver deux
chapitres du livre à ces questions, l’un centré sur les connexions internes, l’autre sur
les connexions externes.
Mais la publication de cet ouvrage ne constitue qu’une des facettes du projet.
L’ambition est aussi :
de mettre en place et alimenter régulièrement un site web de type wiki
évolutif, complétant le livre par des vignettes et proposant des ressources
pour l’enseignement, notamment des exemples de réalisations dans différents
contextes,
d’organiser des conférences et des ateliers Klein où des mathématiciens, des
enseignants, des didacticiens travailleront ensemble, testant les réalisations et
les critiquant, élaborant des contributions.
- 3.1. Les conférences Klein et le projet Klein en langue portugaise
La première conférence a eu lieu à l’université de Madère en octobre 2009 à
l’initiative du CIM (Centre international de mathématiques) et elle a accueilli
environ 100 participants avec une forte proportion de portugais et brésiliens. C’est au
cours de cette conférence qu’est née en fait l’idée de vignette Klein précisée ci-dessous.
La conférence de Madère eut une autre conséquence. Elle fut à l’origine du
projet Klein en langue portugaise. Ce projet, piloté par la Société Mathématique
Brésilienne, et qui implique toutes les sociétés liées au mathématiques ou à leur enseignement au Brésil (une première dans ce pays où les tensions entre
communautés peuvent être particulièrement fortes), vise à assurer la traduction du
livre en portugais, à préparer des ressources en portugais particulièrement adaptées
pour les enseignants brésiliens et à organiser des formations associées pour les
enseignants. Substantiellement financé par le gouvernement brésilien, il a eu ces
deux dernières années un développement exemplaire. L’appel à vignettes lancé a, par
exemple, conduit à la production de près de 80 vignettes. Vingt d’entre elles,
sélectionnées, ont été soumises à l’examen d’enseignants, lors d’ateliers thématiques,
et sont actuellement en cours de révision, suite à cet examen qui sert aussi à identifier
les documents complémentaires nécessaires. Commence à en émerger une littérature
visant à répondre aux besoins mathématiques spécifiques des enseignants qui,
apparemment, n’existait pas ou peu jusqu’ici. Les pilotes du projet reçoivent de plus
en plus de demandes pour organiser de telles formations et les enseignants qui y
participent, très décontenancés au départ par la tâche, inusuelle et difficile de lecture
et d’appropriation d’une vignette, se sentent réellement partenaires du projet, à voir
comment leurs réactions et les commentaires qu’ils produisent à l’issue d’un travail
de plusieurs heures sur ces textes de quelques pages, sont pris en compte.
Depuis cette première conférence, plusieurs autres ont été organisées, comme le
montre le site du projet. La dernière en date, juste après les journées de Grenoble de
l’APMEP, a regroupé une quarantaine de participants à l’AIM (American Institute of
Mathematics) à Palo Alto, et l’essentiel du travail y a été consacré à la discussion et
préparation conjointe de vignettes.
- 3.2.Les vignettes Klein
Comme mentionné plus haut, l’idée de vignette Klein a émergé des discussions
menées lors de la conférence de Madère. De nombreux participants y ont en effet
exprimé le souhait que soit créé un format de contribution qui permette à la fois de
nourrir d’exemples la lecture de chapitres qui seraient nécessairement très
synthétiques, et aussi de favoriser une large participation de la communauté, au-delà
du petit nombre de personnes qui pourraient être impliquées dans l’écriture du livre.
Cette idée a ensuite été précisée par le comité de pilotage pour aboutir à un cahier
des charges des vignettes. Celui-ci est encore susceptible d’évoluer mais on demande
d’abord à une vignette d’être courte (autour de cinq pages et certainement moins de
dix), d’où le choix du terme vignette, donc centrée sur un sujet précis. Elle doit
débuter par un objet technologique, une situation ou un problème, a priori
susceptibles de stimuler l’intérêt professionnel d’un enseignant du secondaire. La
compréhension de l’objet, de la situation ou la résolution du problème doivent
conduire à des mathématiques du 20ème siècle. L’accent doit être mis sur les idées
importantes et il n’est pas question d’y rentrer trop avant dans des détails techniques
pour rester accessible à des enseignants de lycée, mais cependant il nous semble
essentiel que les mathématiques y soient bien visibles. La vignette doit aussi rendre
clair pourquoi le sujet traité est important et ce qu’il est essentiel d’en retenir. C’est
pourquoi nous souhaitons que chaque vignette ait une « morale » et que cette morale
soit explicite. Elle doit enfin fournir des références facilement accessibles, si possible en ligne, permettant d’approfondir la réflexion mathématique et/ou de penser des
exploitations didactiques.
La première vignette, proposée par Bill McAllum, part d’une question posée par
des enseignants américains lors d’une séance de formation : est-ce que deux triangles
qui ont la même aire et le même périmètre sont isométriques ? Contrairement à ce
que l’on pourrait penser, la réponse est : Non. La vignette commence par poser le
problème dans un cas particulier, celui du triangle rectangle de côtés 3, 4 et 5, et
invite le lecteur à y réfléchir, avant de fournir un contre-exemple dont les côtés ont
des mesures rationnelles : 41/15, 101/21 et 156/35, dont on peut légitimement se
demander comment il a pu être trouvé. Comme le montre la traduction de Catherine
Combelles publiée dans le présent dossier, l’auteur montre dans la vignette comment
ce problème élémentaire débouche, via un paramétrage adéquat des triangles, sur
celui de la recherche de points rationnels de courbes elliptiques et comment il peut
être résolu. La morale souligne que les courbes elliptiques jouent un rôle crucial en
théorie des nombres et ont des applications importantes aujourd’hui en
cryptographie, mais aussi que la vignette illustre une idée fondamentale des
mathématiques modernes, celle qui consiste, pour résoudre un problème particulier,
à situer son objet dans un espace plus général et à trouver un moyen approprié de
paramétrer cet espace.
Quand nous avons réfléchi avec Graeme Cohen sur ce que pourrait être le contenu
du chapitre qui, reprenant le titre de l’un des chapitres de l’ouvrage de Felix Klein,
s’intitulerait : Fonctions et analyse, très vite, il nous a semblé que le théorème du
point fixe de Banach devrait y occuper une place importante. Ce théorème qui assure
que, si f est une application contractante dans un espace métrique complet [3] f a un
point fixe unique et que toute suite définie par la récurrence \( u_{n+1}=f(u _{n})\), quel que
soit son premier terme, converge vers ce point [4]
, est, en effet :
un théorème central en analyse à la fois pour assurer l’existence d’objets et
pour les approcher, permettant par là-même d’établir des connexions entre
travail qualitatif et quantitatif en analyse,
un théorème déjà présent, au moins implicitement, dans l’enseignement
secondaire dans le contexte de fonctions d’une variable réelle mais dont
l’extension aux espaces fonctionnels montre la puissance de l’analyse
développée au 20ème siècle,
un théorème qui a des applications diverses, à la fois internes et externes aux
mathématiques,
un théorème, enfin, qui permet de revisiter des situations mathématiques
connues et d’établir des connexions entre des mathématiques très anciennes
et des mathématiques très actuelles.
M’inspirant de mon expérience de didacticienne (Artigue, 2001), d’enseignante
d’analyse au CAPES et de formations mathématiques d’ouverture mises en place
pour les PLC2 avec Thierry Raoult, lorsque je travaillais à l’IUFM de Reims, j’avais
alors envisagé une vignette qui débuterait par la question suivante :
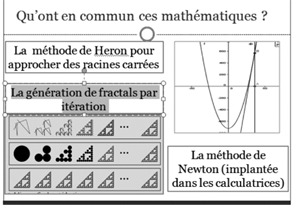
La méthode de Heron pour approcher les racines carrées, remonte au 3ème siècle de
notre ère. Elle est familière aux enseignants de lycée français car elle est proposée
dans la plupart des manuels de terminale, dans le chapitre consacré à l’étude des
suites. Nous reproduisons ci-après, ce qui n’est en revanche pas le cas dans les
manuels, sa présentation initiale dans les Métriques de Heron à partir de l’extrait
traduit par J.P. Levet proposé dans (Chabert, 2010). Il s’agit de déterminer le côté
d’un carré d’aire 720.
« Puisque 720 n’a pas de côté rationnel, nous extrairons le côté avec une très petite
différence de la façon suivante. Comme le premier nombre carré plus grand que 720
est 729 qui a pour côté 27, divise 720 par 27, cela fait 26 et \( \frac{2}{3}\) , ajoute 27 cela fait \(53\frac{2}{3}\)
; prends-en la moitié, cela fait 26\( \frac{1}{3}x \frac{1}{3}\) . En fait, 26\( \frac{1}{3}x \frac{1}{3}\) multiplié par lui-même
donne 720 \( \frac{1}{36}\) ; de sorte que la différence (sur les carrés) est \( \frac{1}{36}\) . Si nous voulons
rendre cette différence inférieure encore à \( \frac{1}{36}\), nous mettrons 720 trouvé tout à
l’heure à la place de 729 et, procédant de la même façon, nous trouverons que la
différence (sur les carrés) est beaucoup plus petite que \( \frac{1}{36}\). »
Exprimée en langage actuel, la technique d’approximations successives décrite par
Heron consiste à considérer la suite \(u_n\) définie par \(u_{n+1}=\frac{1}{2}\left(u_{n}+ \frac{720}{u_{n}}\right)\) et \(u_{0}
= 27\).
Cette suite, comme le laissent supposer les valeurs des premiers termes obtenues
avec la calculatrice symbolique TI-nspire reproduites ci-dessous, converge très
rapidement.

Figure 1 : Premiers termes d’une suite de Heron
Le lecteur notera que, si les valeurs approchées affichées ne permettent déjà plus de
séparer \(u_3\) et \(u_4\), ce n’est pas le cas des valeurs exactes, et que le nombre de chiffres
des dénominateurs semble quasiment doubler d’un terme au suivant.
Quel lien existe-t-il entre cette méthode, connue dès l’antiquité, et la méthode de
Newton, déjà bien plus récente même si elle remonte à plusieurs siècles, et qui est
implantée dans ces mêmes calculatrices, pour résoudre de façon approchée des
équations mises sous la forme f(x) = 0, justement parce qu’elle a des propriétés de
convergence très intéressantes ? La méthode de Newton consiste, rappelons-le,
partant d’une valeur approchée de la racine cherchée, à remplacer la courbe \(C_f\) par sa
tangente au point ayant pour abscisse cette valeur approchée (tangente supposée
exister et être non horizontale). L’intersection de la tangente avec l’axe des abscisses
donne alors une nouvelle valeur approchée de la racine, en général bien meilleure, et
l’on peut itérer le processus. Si l’on considère la fonction \(f(x) = x^{2} - 720\), et si l’on
prend comme valeur approchée initiale \(u_0\) non nul, l’équation de la tangente à \(C_f\) au
point d’abscisse \(u_0\) est : \(y-f(u_{0})= f’(u_{0})(x-u_{0})\) et comme \(f’(u_{0}) = 2u_0\) est non
nul, son intersection avec l’axe des abscisses est le point d’abscisse
\(u_{1}= u_{0}\frac{f(u_{0})}{f’(u_{0}}\)
.
En remplaçant f et f ’ par leurs valeurs, on constate que l’on obtient exactement la
suite de Heron. La méthode de Heron peut donc être vue aujourd’hui comme une
instanciation particulière de la méthode de Newton.
Les mathématiques engagées jusqu’ici ne sont pas des mathématiques du vingtième
siècle et le théorème du point fixe n’y est pas intervenu. Mais son intervention éclaire applications contractantes, et même fortement contractantes. Supposons en effet que
f soit une fonction de classe \(C^2\) sur un intervalle I où f ’ne s’annule pas, I étant de
centre \(\alpha\) tel que \(f( \alpha) = 0\), et soit la fonction g définie sur I par \(g(x) = x.\frac{f(x)}{f’(x)}\)
La
fonction g est dérivable sur I et g’ est continue sur I et
\(g’( \alpha) =0\) . Donc, pour tout k positif et strictement inférieur à 1, il existe un sous-intervalle
J de I centré lui aussi en \(\alpha\) sur lequel g’ est en valeur absolue inférieure à
k et donc, par le théorème des accroissements finis, g est contractante de rapport k.
Alors l’intervalle J est stable par g et, pour tout \(u_0 \) de J, la suite définie par \(u_{n+1}=g(u\n)\)
converge vers \(\alpha\). De plus, pour tout n, \(\mid u_{n}-\alpha\mid\leq k^{n}\mid u_{0}-\alpha\mid\) ce qui
explique la convergence extrêmement rapide observée. \(\alpha\) est ce que la théorie des
systèmes dynamiques appelle un point fixe super-attractif. Mais cette théorie, qui
s’est particulièrement développée dans la deuxième moitié du vingtième siècle, nous
montre aussi que, si \(u_0\) n’est pas convenablement choisi, les dynamiques de ces suites
de Newton peuvent être en revanche très complexes et de nature chaotique. Nous
renvoyons le lecteur à l’excellent article de Tan Lei sur ce thème paru sur le site
Images des Mathématiques
Même si nous avons fait un lien dans ce dernier paragraphe entre les méthodes de
Heron, de Newton et des mathématiques du vingtième siècle, nous en sommes restés
à des fonctions d’une variable réelle, celles que l’on manipule au lycée.
Mais, comme
souligné plus haut, le théorème du point fixe a un champ d’application bien plus large
et c’est à une incursion dans cette direction que nous invite le troisième contexte
évoqué dans la question initiale, celui de la génération itérative de fractals. Les trois
images qui la composent, extraites de (Fisher, 1995) évoquent en effet une
convergence vers un objet géométrique ressemblant à un triangle de Sierpiński qui
est un objet fractal. Et ce que ces images semblent nous indiquer, c’est que, quelle
que soit la figure initiale (comme précédemment nous pouvions affirmer, quel que
soit le choix de \(u_0\)), la suite créée converge vers une même figure qui est un point fixe
pour cette suite. Y a-t-il derrière ce phénomène encore une fois une application
contractante, et si oui laquelle ? La transformation f qui permet de passer d’une figure
à la suivante est, en fait, une simple combinaison de trois transformations affines : la
figure est soumise à une homothétie de rapport ½ puis trois translations sont
effectuées pour obtenir trois copies de cette réduction. Si l’on considère les figures
inscrites dans un carré de côté 1 centré à l’origine, les trois transformations
mobilisées sont les suivantes :
\(f_1 : (x,y)\rightarrow \left(\frac{x}{2} +\frac{1}{4}, \frac{y}{2} +\frac{1}{4} \right) \)
\(f_2 : (x,y)\rightarrow \left(\frac{x}{2} +\frac{1}{4}, \frac{y}{2} -\frac{1}{4} \right) \)
\(f_3 : (x,y)\rightarrow \left(\frac{x}{2} -\frac{1}{4}, \frac{y}{2} -\frac{1}{4} \right) \)
Et à une partie A du carré, on associe par l’application f :
\(f(A) = f_{1}(A) \cup f_{2}(A)\cup f_{3}(A)\).
À première vue, cette application ne semble pas particulièrement contractante, il faut
donc travailler un peu plus pour éclairer la dynamique de cette situation par le
théorème du point fixe. Dans la vignette Klein qu’elle a réalisée sur ce thème du
point fixe, vignette qui suit un scénario un peu différent de celui proposé ici,
Christiane Rousseau essaie de donner une idée de la métrique appropriée sur les
parties fermées et bornées du plan (la métrique de Hausdorff) sans rentrer dans des
détails trop techniques, de la façon suivante. Pour deux telles parties du plan, \(A_1\) et
\(A_2\), elle commence par donner sens à la relation \(d_{H}(A_{1},A_{2})\leq\epsilon \), pour \( \epsilon > 0\) en
expliquant que cela veut dire que si notre œil a une précision de \(\epsilon\), il lui est
impossible de distinguer \(A_1\) de \(A_2\), ce qu’elle formalise ensuite de la façon suivante :
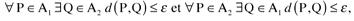
d désignant la distance euclidienne usuelle dans \(\mathbb{R}^{2}\).
Elle définit ensuite, de façon indirecte, la distance de Hausdorff entre deux
ensembles fermés bornés du plan comme l’inf de tous les \(\epsilon\) positifs tels que cette
relation ci-dessus soit satisfaite [5]. Avec cette définition, on peut montrer que
l’application f considérée ci-dessus est contractante de rapport ½. Ce qui explique
l’impression visuelle très rapide de convergence vers un triangle de Sierpiński.
Au-delà de leur exploitation pour la génération de fractals, ces techniques itératives
ont aussi été utilisées dans la compression d’images mais elles restent pour l’instant
assez peu performantes (Rousseau & Saint Aubin, 2008).
3.3. En conclusion
Je m’arrêterai là pour ce qui est du projet Klein qui, jusqu’ici, a progressé beaucoup
plus lentement que nous ne l’espérions au début. Car même si le projet suscite un très
grand intérêt chaque fois qu’il est présenté, l’écriture de textes répondant aux
ambitions que nous nous sommes données, et accessibles à des enseignants dont la
formation et la culture mathématique peuvent être très divers suivant les régions du
monde et les cultures éducatives, ne va en rien de soi. J’espère cependant que cette
brève présentation suscitera des propositions de vignettes de la part des lecteurs du bulletin, ainsi que des suggestions pour améliorer les vignettes existantes et aussi
pour enrichir les références associées, notamment par des exemples de réalisations
avec les élèves ou en formation.
S’agissant de formation, je retiens notamment du travail mené jusqu’ici que les choix
à effectuer, quand on se donne le projet de rendre des mathématiques récentes et
actuelles sources d’inspiration pour les enseignants, doivent peser différentes
potentialités et, en particulier, les suivantes :
le potentiel épistémologique : les idées mathématiques et métamathématiques
que le thème permet de rencontrer, travailler, approfondir, de façon
accessible,
le potentiel didactique : les connexions avec les mathématiques du secondaire
(contenu, éclairage de difficultés d’élèves, questions curriculaires, …),
le potentiel pratique : les pratiques et techniques mathématiques que le travail
sur le thème engage, permet de consolider et développer,
le potentiel de connexion : les connexions que le thème permet entre points
de vue, domaines,
le potentiel de défi : le potentiel offert pour questionner des visions
communes, étonner, susciter l’intérêt,
le potentiel culturel : le potentiel pour refléter les mathématiques comme
aventure humaine et comme science vivante.
Enfin, il me semble important de souligner que, même s’il peut à terme aider à
construire des liens entre mathématiques actuelles et enseignement des
mathématiques, le projet Klein ne couvre que très partiellement les besoins
nécessaires. Car, comme je le soulignais au départ, il ne suffit pas de montrer que des
synergies sont possibles, il faut penser les stratégies qui permettront de les faire vivre
dans la réalité de la formation des enseignants et dans la réalité des classes. Et ceci
me conduit à revenir sur le type de déclaration que j’évoquais au début de ce texte
quand j’écrivais : « Il est aussi fréquent d’entendre dire que, comparativement,
l’enseignement ne donne aujourd’hui à voir et à pratiquer aux élèves que des
mathématiques vieilles de plusieurs siècles, sinon de millénaires, bref une science
morte et ce, avec des pratiques elles aussi inchangées, que les liens sont coupés. »
Est-ce vraiment le cas ?
4. Mathématiques actuelles et enseignement : la vision curriculaire
S’agissant du curriculum, il faut bien sûr distinguer entre ce qui est prescrit (le
curriculum visé) et la réalité du terrain (le curriculum réel). Si l’on considère le
curriculum visé, pour ce qui est de la France et pour de nombreux autres pays, il est
difficile d’adhérer à l’affirmation reproduite ci-dessus. Les efforts faits pour
rapprocher les mathématiques enseignées des mathématiques actuelles y sont
indéniables. Ceci concerne les contenus comme les pratiques. Je ne chercherai pas à
être exhaustive et me bornerai à souligner un certain nombre d’évolutions qui m’en
semblent particulièrement caractéristiques :
la place croissante accordée aux statistiques et probabilités, depuis la réforme
des lycées de 2000,
l’introduction de domaines comme la théorie des graphes, dans cette même
réforme,
l’accent mis sur l’algorithmique,
les thématiques proposées pour la spécialité Mathématiques en classe de
Terminale dans le cadre de la nouvelle réforme des lycées, notamment dans la
partie relative aux matrices et aux suites,
la mise en place de dispositifs spécifiques exigeant l’interdisciplinarité au
lycée avec les TPE en première dans la réforme de 2000 et le nouvel
enseignement d’exploration MPS en seconde depuis 2010 [6], avec des
horaires conséquents,
l’accent mis sur les démarches expérimentales en mathématiques, même si
l’épreuve expérimentale de mathématiques au baccalauréat n’a finalement
jamais réussi à dépasser elle-même le stade expérimental, sur la modélisation,
sur les démarches d’investigation et de projet, tout cela en s’appuyant sur les
potentialités offertes par la technologie.
Je pourrais entrer davantage dans les détails et multiplier les citations de textes
officiels pour appuyer mon discours, mais je ne pense pas que ce soit nécessaire pour
un lecteur du Bulletin de l’APMEP. Aujourd’hui, par exemple, si l’on regarde un
domaine comme celui des statistiques, les programmes français sont sans doute
parmi les plus ambitieux pour l’enseignement secondaire. Les thèmes qui sont
proposés pour le nouvel enseignement de la spécialité mathématiques concernent
pour plusieurs d’entre eux des mathématiques du XXème siècle (principes du calcul
de pertinence d’une page web, modèles de diffusion, modèles proie-prédateur). En
fait, ce sont les mathématiques classiques, et notamment la géométrie, qui ont fait les
frais de cette évolution, qui se combine avec des réductions horaires.
Les élèves, pour
ne citer qu’un exemple, sortiront du nouveau lycée sans avoir rencontré
officiellement d’autres transformations géométriques que les symétries, au début du
collège, et faiblement les translations. Et après l’enseignement de la géométrie, c’est
celui de l’analyse qui est drastiquement réduit dans la dernière réforme en série
scientifique et perd la cohérence et consistance qu’avait essayé de lui redonner la
réforme du lycée de 2000.
Si l’on considère les textes, le problème n’est donc pas en France celui d’un
enseignement des mathématiques qui serait par essence figé, dans ses contenus et
dans ses pratiques. C’est plutôt celui d’un enseignement à qui l’on demande de
bouger, et même de bouger beaucoup, sans vouloir souvent considérer ce que ces
changements nécessitent pour être viables, pour que puissent s’amorcer et se
développer des dynamiques d’évolution productives, et sans se donner les moyens
jusqu’ici d’étudier sérieusement les dynamiques réelles que l’on ne peut que très partiellement anticiper, pour apporter les régulations nécessaires, répondre aux
besoins de formation, produire des ressources adaptées [7].
C’est celui de la
multiplication des dispositifs d’enseignement et des intervenants, les problèmes de
cohérence qui en résultent, de plus en plus ressentis par les enseignants. C’est celui
d’une formation continue sinistrée alors que les évolutions engagées la rendent
d’autant plus nécessaire, et dont les maigres moyens sont de plus pompés par la
nécessité de faire fonctionner une réforme catastrophique de la formation initiale
(Arnoux, 2011).
Il existe bien sûr des réussites locales et tous ceux qui travaillent, notamment au sein
des IREM, de l’APMEP ou de l’IFÉ (Institut Français d’Education) qui a succédé à
l’INRP, peuvent en faire état. Je me bornerai à citer, pour ne prendre que quelques
exemples récents, le recensement effectué par la Commission inter-IREM Lycées des
travaux des IREM concernant l’algorithmique qui va prochainement donner lieu à
une publication inter-IREM et montre la richesse des documents produits par la
communauté pour accompagner cette évolution curriculaire, le dossier coordonné par
Catherine Combelles et publié avant même la fin 2011 dans le Bulletin de l’APMEP
concernant l’enseignement MPS (Combelles, 2011), les travaux menés au sein des
groupes associés à l’IFÉ : e-Colab, Exprime ou le groupe CDAmpères issu de la
commission inter-IREM Didactique [8], et concernant ce dernier, notamment, la série
de brochures publiées par l’IREM de Poitiers pour le collège et maintenant la
seconde (cf. par exemple (Chevalarias, T. & al., 2009), (Chevalarias, N.& al., 2011),
pour soutenir un enseignement décloisonné qui se développe à partir de questions à
fort pouvoir générateur (des parcours d’étude et de recherche au sens de la théorie
anthropologique du didactique (Chevallard, 2007)). Mais, ce que montrent aussi ces
réalisations, c’est la difficulté de faire face aux multiples contraintes (comment par
exemple rendre l’interdisciplinarité effective en MPS si les enseignants de disciplines
différentes ne peuvent jamais travailler ensemble avec les élèves ?), c’est
l’investissement demandé que, seul, le soutien d’une communauté a rendu
acceptable. Dans les secteurs les plus fragiles de notre système éducatif, ces
changements en cascade peuvent simplement détruire des équilibres, certes
insatisfaisants mais qui avaient le mérite d’exister. Car l’on sent bien combien la
création de synergies productives ne peut se faire sans faire l’effort de construire de
nouvelles cohérences, aussi attentives aux domaines classiques et à la façon dont
l’évolution des connaissances et celle des pratiques peut inspirer l’évolution de leur
enseignement qu’aux nouveaux domaines, thèmes, questionnements que l’on
souhaite introduire, et attentives aussi à leurs interactions possibles.
Les sciences
mathématiques, nul ne saurait le nier, ont plus que les autres sciences une dimension cumulative, et il ne faudrait pas que la recherche de synergies entre les
mathématiques qui s’enseignent et les mathématiques qui se font, conduise à la
déshérence des domaines classiques ou à un enseignement où l’évolution des
pratiques serait réservée aux domaines et aux dispositifs nouvellement introduits.
Ces problèmes, comme tous ceux qui concernent de façon générale l’éducation, ne
sont en aucun cas faciles à résoudre, et je voudrais dans les lignes qui suivent élargir
mon propos au-delà de la seule question des synergies entre mathématiques qui se
font et mathématiques qui s’enseignent. L’évolution du système éducatif est pour
nous tous, aujourd’hui, source d’inquiétude et nous avons l’impression que loin
d’avancer vers la résolution des problèmes existants, nous voyons les obstacles et les
difficultés s’accumuler. Faut-il pour autant sombrer dans le catastrophisme et
idéaliser les temps bénis où, par exemple, les horaires étaient bien plus conséquents,
où la filière scientifique débutait dès la classe de seconde ? Je ne le pense pas. Quand
je vois le rapport que la plupart de nos intellectuels, de nos hommes politiques, des
journalistes ont aux mathématiques, pour ne citer qu’eux car ils sont les plus
médiatiquement visibles, je ne peux m’empêcher de me dire qu’en dépit des moyens
dont nous avons longtemps disposé pour l’enseignement des mathématiques, nous
avons partiellement échoué (ce faisant je ne m’adresse pas bien sûr à ceux qui entrent
aujourd’hui dans la carrière ou y sont rentrés récemment). Nous avons sans aucun
doute réussi à former des scientifiques et des mathématiciens de qualité, mais nous
avons échoué à assurer une formation mathématique, peut-être modeste mais
néanmoins de qualité, à des centaines de milliers si ce n’est des millions d’élèves
auxquels elle était pourtant accessible. Nous avons échoué à faire que, pour eux, les
mathématiques soient un instrument de questionnement et d’intelligibilité du monde,
et non pas une simple discipline scolaire [9]. Nous avons échoué, sans doute parce
que nous n’avons pas suffisamment compris que c’était là notre première mission,
que nous avons trop vite accepté l’échec, le manque de motivation de nos élèves,
peut-être aussi parce que la pression de la société sur nous n’a pas été assez forte.
Aujourd’hui la situation est toute différente. Le socle commun veut changer le
contrat social de l’école et, dans le même temps, les conditions faites à
l’enseignement des mathématiques sont de plus en plus difficiles.
Pourtant, ce que
nous n’avons pas réussi à faire du temps des vaches grasses, nous devons le tenter
aujourd’hui et nous devons nous battre pour le réussir. Ce défi, je pense que nous
pouvons le relever. Il y a à cela de multiples raisons, mais une essentielle est que nous
disposons aujourd’hui de connaissances sur l’enseignement et l’apprentissage, sur le
fonctionnement des systèmes didactiques qui modifient profondément les outils dont
nous disposons pour penser l’enseignement et tirer le meilleur profit de nos marges
de manœuvre, ainsi que pour montrer la nécessité d’autres formes de pilotage pour
le système éducatif. À ceci s’ajoute que, grâce à l’évolution technologique, de plus
en plus, presque partout dans le monde, on peut avoir aujourd’hui accès à des
ressources de qualité, on peut mutualiser les connaissances, et des collaborations peuvent s’organiser moins dépendantes de la proximité géographique immédiate.
La
vision collaborative du métier d’enseignant, de la conception de ressources progresse
d’ailleurs, même dans une culture comme la nôtre qui y est si peu préparée,
comparativement à d’autres. Si nous pouvons relever ce défi, c’est parce que nous ne
sommes pas les seuls à vouloir réaliser cette ambition d’un enseignement
mathématique de qualité pour tous et que d’autres peuvent nous y aider.
C’est cette
solidarité entre communautés, c’est cette énergie, cette volonté et créativité dans les
contextes les plus difficiles que j’ai éprouvée, année après année, au sein d’ICMI et
qui nourrit un optimisme que certains trouveront peut-être démesuré dans les
circonstances actuelles, et la volonté de continuer à marcher, comme nous y ont
incités ces journées nationales de l’APMEP.
Références
Arnoux, P. (2011). La mastérisation de la formation des enseignants. Tangente
Éducation, no 18, 8-11.
Artigue M. (2001). L’entrée dans le champ conceptuel de l’analyse : - réformes
curriculaires, recherches didactiques, où en est-on ?, in T. Assude et B. Grugeon
(eds), Actes du Séminaire National de Didactique des Mathématiques, année 2000,
p. 277-301.
Artigue, M. (coord.) (2011). Les défis de l’enseignement des mathématiques dans
l’éducation de base. Paris : UNESCO.
http://unesdoc.unesco.org/images/0019/001917/191776F.pdf
Chevalarias, T. & al. (2009). Enseigner les mathématiques en sixième à partir des
grandeurs : les angles. IREM de Poitiers.
Chevalarias, N.& al. (2011). Enseigner les mathématiques en seconde : trois parcours
sur les fonctions. IREM de Poitiers.
Chevallard, Y. (2007).Les mathématiques à l’école : pour une révolution
épistémologique et didactique. Bulletin de l’APMEP, no 471, 439-461.
Combelles, C. (coord.) (2011). Dossier MPS. Bulletin de l’APMEP, no 495, 392-455.
Fisher, Y. (1995). Fractal Image Compression, Theory and Application. Berlin :
Springer Verlag.
Klein, F. (1924).Elementarmathematik von hölteren Standpunkte aus. Arithmetik,
Algebra, Analysis. Berlin : Springer (English translation by E.R. Hedrick and C.A.
Noble of the third edition, Macmillan, New York, 1932).
Lovász, L. (2007). Trends in Mathematics, and How they could Change Education ?
Conférence Européenne « Le Futur de l’Education Mathématique en Europe »,
Lisbonne, Décembre 2007. http://www.cs.elte.hu/~lovasz/lisbon.pdf.
Rousseau, C., Saint –Aubin, Y. (2008). Mathématiques et Technologie. Springer
Verlag.
Schubring, G. (2011). Conceptions for relating the evolution of mathematical
concepts to mathematical learning – epistemology, history, and semiotics interacting.
Educational Studies in Mathematics, Vol. 77.1, 79-104.
<redacteur|auteur=13>































