François Lo Jacomo

Résumé de l’article

Suite de la correction des problèmes de l’Olympiade Internationale 2001 (cf. Bulletin Vert n° 435).

Enoncé 4 : problème du magicien (était-il facile ?)
Un magicien a cent cartes numérotées de 1 à 100. Il les répartit dans trois boîtes, une
rouge, une blanche et une bleue, de telle sorte que chaque boîte contienne au moins
une carte.
Un spectateur choisit deux de ces trois boîtes, tire une carte dans chacune d’elles et
annonce la somme des nombres figurant sur les cartes tirées. Connaissant cette
somme, le magicien identifie la boîte dans laquelle aucune carte n’a été tirée.
De combien de façons le magicien peut-il répartir les cartes dans les boîtes de telle
sorte que ce tour de magie réussisse toujours ? (Deux façons de
répartir les cartes
sont considérées comme différentes si au moins une carte est placée dans deux boîtes

Enoncé 5 :
Existe-t-il un entier strictement positif n tel que : n soit divisible par exactement 2 000 nombres premiers distincts et \(2^{n+1}\) soit divisible par n

Enoncé 6 : triangle inscrit dans le cercle inscrit.

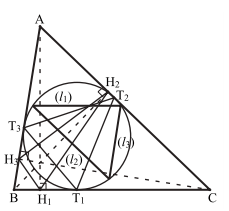
Soient \(AH_1\) , \(BH_2\), \(CH_3\) les hauteurs d’un triangle ABC dont tous les angles sont aigus. Le cercle inscrit dans le triangle ABC est tangent respectivement aux côtés
BC, CA, AB en \(T_1\), \(T_2\), \(T_3\). On désigne respectivement par \(l_1\), \(l_2\), \(l_3\) les symétriques des droites \(H_2H_3\), \(H_3H_1\) , \(H_1H_2\) par rapport aux droites \(T_2T_3\), \(T_3T_1\),
\(T_1T_2\). Montrer que \(l_1\), \(l_2\), \(l_3\) déterminent un
triangle dont les sommets appartiennent au cercle inscrit dans le triangle ABC.

 Télécharger l’article en pdf dans son intégralité
<redacteur|auteur=500>