Au moyen de murs additifs ,

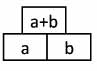
utilisés plus habituellement pour des calculs numériques, et que l’on pimentera un peu pour les enrichir par la suite, il s’agit d’introduire une ou plusieurs variables qui permettront d‘expliquer, de justifier les phénomènes observés, de façon non seulement plus courte et économe mais aussi plus définitive. Quoi de plus catégorique que 2 et 2 font 4 ?
On tache alors de mettre à profit le procédé …
L’article propose également des fichiers exerciseurs pour les élèves, créés avec le tableur d’Open Office muni de l’extension CmathOOoCAS.

2 exemples connus (abordables dès la 5e)

 A

D’éventuelles explications rhétoriques sont possibles pour justifier que : « il faut placer les plus grands au milieu ». L’introduction de l’algèbre les complète. On obtient aisément

au sommet à partir des 4 nombres a, b, c et d pris sur la ligne de base. Cette formule confirme naturellement la conjecture.

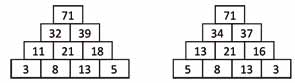
Et à y regarder de plus près, elle montre également les rôles symétriques de a et d et de b et c ; répondant ainsi au « moi aussi j’ai trouvé 71, mais autrement ! »

Autre qualité et pas des moindres, les nombres peuvent être changés. Et particulièrement ils peuvent être relatifs !

L’introduction des lettres fait mieux qu’avaliser la conjecture, elle la démontre et ouvre de nouvelles perspectives.

 B

Débutant dans l’algèbre, l’élève n’identifie pas encore la tâche à une équation et d’ailleurs il n’écrira généralement pas 8a = 136 après avoir obtenu

au sommet ; mais effectuera la division de 136 par 8 [1]

On peut aussi montrer que c’est a+3a+3a+a, en référence à l’exemple précédent. C’est précisément cette similitude d’approche qui me semble intéressante car mon but n’est pas ici la résolution d’équation mais le travail d’addition, de soustraction et de simplification d’écritures algébriques simples, tel que celui qui suit.

Un 3e exemple

.

Ayant constaté que le résultat au sommet est indépendant du choix initial, la confirmation sans recours à l’algèbre est ici « quasi » impossible.

Et ensuite

Ce troisième exemple va être générique de gammes se voulant ni trop fastidieuses ni trop virtuoses ; à concevoir comme celles du calcul mental c’est-à-dire des gammes d’assouplissement. Pour cela il faut spécialiser certaines briques des murs.

On peut par exemple proposer

Les pyramides qu’auront à compléter les élèves garderont la propriété d’avoir un sommet indépendant du choix initial [2]. En voici quelques unes :

nota : en classe, j’utilise plutôt des couleurs que des hachurages

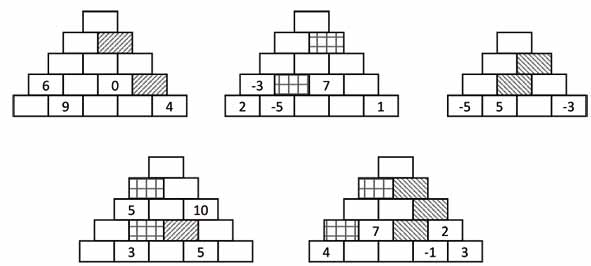
À l’épreuve de la pratique, les avantages supposés pour les élèves, tels que accroche, intérêt, connaissance du résultat à obtenir, recherche des erreurs quand on ne l’obtient pas, s’avèrent réels. De plus il me semble rencontrer moins fréquemment qu’auparavant l’épouvantable 15n en lieu et place de 12n + 3.

La limite au genre est apparue se situer à des pyramides de 5 étages. Au-delà, la tâche devient trop pesante, les erreurs plus nombreuses.
Je m’en suis tenu à l’utilisation d’entiers relatifs et des basiques 2(a+b), -(a+b) et -2(a+b) afin de ne pas trop tirer sur une ficelle qui perdrait peut-être alors de sa rentabilité.

CmathOOoCAS

Voir sur internet
, un plus bien agréable

Conçu et développé par Christophe Devalland, CmathOOoCas est une extension qui permet le travail du calcul formel sur le tableur d’Open Office. Des murs préétablis peuvent ainsi être complétés numériquement ou algébriquement. J’ai créé des fichiers exerciseurs qui peuvent être utilisés en salle informatique ou à la maison. La fonction ALEA ENTRE BORNES, utilisée entre -10 et 10 de façon interne par l’exerciseur, renvoie des nombres fixés différents, a priori …, pour chaque élève. Ils peuvent, à loisir, tester des valeurs numériques ou s’aventurer immédiatement au calcul littéral.

Il y a 4 fichiers sur les murs. Un premier qui montre en exemple le fonctionnement, suivi d’un pour chaque type de cases colorées (et pas hachurées).

Un 5e et dernier fichier propose de compléter cette fois-ci une spirale numérique. Le principe en est sensiblement le même et a pour but de simplifier des expressions algébriques, justifiant ainsi les visibles – et vues – régularités ou patterns qui apparaissent à l’issue du calcul numérique préalable. Il s’agit d’un exercice que j’aborde déjà en 5e.

Ces 5 fichiers sont téléchargeables.
J’ai essayé de les faire aussi interactifs que possible, mais n’étant pas un spécialiste de la chose, ils sont assurément améliorables, complétables, … Si vous vous y lancez, n’hésitez pas à me faire connaître vos améliorations, vos interrogations, etc.
 

 
Cette activité est le fruit d’une réflexion sur une entrée dans l’algèbre non directement par les équations. Une source d’inspiration toute particulière en est la brochure Enseignons en jouant, (B. HONCLAIRE, N. LAMBELIN, G. et Y. NOËL) de nos collègues belges de la SBPMef que l’APMEP propose sous le numéro 880.

Elle constitue une véritable mine !