Un texte de 1969... Première étape... vers une réforme de l’enseignement mathématique dans les classes élémentaires. Supplément au Bulletin de l’APMEP n° 269
Pourquoi nous publions cette brochure
L’école élémentaire est actuellement en quête d’une nouvelle manière d’être dont l’institution du « tiers-temps » avec l’introduction massive de l’éducation physique ne sont pas les moindres signes. Les raisons essentielles de cette mutation ont été mises en évidence par la Commission Ministérielle de Rénovation Pédagogique, de façon assez convaincante pour que les propositions exprimées par cette Commission dans son rapport de synthèse ne restent pas lettre morte. Nous nous en réjouissons.
Dans ces perspectives, la réorganisation de l’enseignement du a calcul » que nous souhaitions depuis longtemps, va enfin pouvoir être mise en œuvre. Au printemps de cette année 1g6g, la Commission que préside le Pr Lichnérowicz, et qui depuis 1966 s’est vu confier la tache de définir les contenus, les méthodes, les moyens d’un enseignement mathématique conforme aux exigences et aux possibilités de notre époque, partout et à tous les niveaux, s’est précisément consacrée au niveau élémentaire, point de départ de l’éducation en mathématique comme en tout autre domaine [1]
Le souci de présenter des propositions applicables dès la rentrée 1969, a conduit les membres de la Commission à s’attacher en premier lieu à l’élaboration d’un programme de formation initiale des futurs instituteurs, ainsi qu’à une nouvelle rédaction des programmes de 1945 accompagnée de commentaires assez nourris pour éclairer la réforme déjà possible.
Un projet concernant la formation des maîtres en exercice (mise à jour et formation permanente) est également à l’étude. Et il reste à élaborer un véritable programme qui montrera nettement ce que l’enseignement élémentaire peut et doit apporter aux enfants, dans la perspective d’une formation mathématique de conception a moderne », et à envisager l’échelonnement dans le temps de l’application d’un tel programme.
Nous remercions le Pr Lichnérowicz, de nous autoriser à publier les deux premières parties du rapport, adoptées fin juin par la Commission.
Les délais administratifs trop habituels n’ont pas permis la publication officielle de ces textes avant la rentrée scolaire. Elle ne saurait tarder paraît-il, mais il nous est agréable de répondre aux demandes qui nous sont adressées de toutes parts, en faisant connaître ces documents dès maintenant à tous les maîtres qui souhaitent s’en inspirer déjà pour la conduite de leur classe, à ceux qui acceptent de se remettre à l’étude pour dominer l’évolution ainsi engagée. Le programme destiné aux élèves-maîtres de 4° et 5° année, doit effectivement fournir les thèmes de travail pour la mise à jour des connaissances de tous.
Le texte proposé pour les programmes des classes élémentaires concorde avec le projet " A " présenté par un groupe de collègues de notre Association et adopté à l’Institut Pédagogique National par l’ensemble des animateurs des expériences en cours, lors des réunions de décembre et janvier 1968-69 [2]
.
Ce texte se borne à redistribuer et alléger le contenu des programmes de 1945. La rédaction en trois paragraphes pour les C.E. et C.M. souligne la distinction entre les notions mathématiques dont il convient d’organiser l’approche et d’autres domaines d’activités qui leur sont en partie étrangères : observation de l’espace et familiarisation avec des objets « géométriques » ; pratique de mesures, étude d’objets et de phénomènes physiques mesurables. A ce propos, les soucis « pratiques » qui pesaient lourdement sur les textes de 1945 (prix et poids à l’unité..., peintures et tapisseries etc.) n’apparaissent plus dans la rédaction proposée. Bien sûr, il convient de faire appel au besoin à des exemples tirés de situations familières pour mettre en jeu des notions mathématiques, mais le but de l’enseignement mathématique n’est pas de fournir telle ou telle réponse à telle ou telle question « pratique », comme on a pu le croire. C’est en fait de fournir des modes et des outils de pensée plus puissants, capables de s’appliquer à des situations imprévues, et avant tout de construire ces outils.
A ce projet immédiat nous avions alors associé un projet "B" plus élaboré, qui servira probablement de référence, de la même façon, pour l’élaboration du nouveau programme envisagé par la Commission. Il nous paraît donc utile de
publier de nouveau ce projet, dans sa forme primitive (où l’on a simplement fait apparaître les idées essentielles sans chercher à soigner la rédaction).
L’année scolaire 1969-70 voit l’application générale de la réforme de l’enseignement mathématique dans le second degré aux niveaux des classes de Sixième et de Seconde. Sept académies (Paris, Strasbourg, Lyon, Rennes, Besançon, Bordeaux, Aix-Marseille) vont cette année bénéficier de la création des I.R.E.M. pour l’animation des recherches et des expériences pédagogiques, ainsi que pour la formation des maîtres. Partout notre Association s’efforce, en multipliant les réunions entre les professeurs, de faciliter cette formation et d’assurer la réussite de la réforme.
L’école élémentaire ne doit plus rester en marge d’un tel mouvement. Comme dans tant d’autres pays, engagés eux-aussi dans la même évolution (Danemark, Grande-Bretagne, Allemagne, etc.), ces premières années d’école peuvent offrir
à nos enfants les activités mathématiques les plus stimulantes, les plus efficaces, les plus riches d’avenir... Beaucoup d’efforts seront nécessaires pour réaliser partout ces objectifs.
Une première étape est une manière sage et sûre d’avancer tout en préparant la suivante, et d’amorcer ainsi la réforme permanente grâce à laquelle l’école, maison de toute la jeunesse, saura répondre toujours mieux à sa mission.
Mme M.-A. TOUYAROT, Présidente de l’A.P.M.E.P.
Commission ministérielle
sur l’enseignement des mathématiques
Rapport des sous-commissions 3 et 4 de l’enseignement élémentaire
(Paris, le 30 Juin 1969)
- 1. Recommandations en vue d’une action immédiate
L’enseignement mathématique à l’école élémentaire veut répondre
désormais aux impératifs qui découlent d’une scolarité obligatoire prolongée
et de l’évolution de la pensée mathématique elle-même.
Il s’agit alors de faire en sorte que cet enseignement contribue au meilleur
développement de tous les enfants de six à onze ans, dans le but de donner
à tous les mêmes chances de succès dans le premier cycle secondaire et non
plus de les préparer directement à la vie active.
L’ambition essentielle de cet enseignement n’est plus en premier lieu
de faire acquérir des techniques de résolution de problèmes catalogués suggérés
par “la vie courante” . Les notions mathématiques liées à ces techniques
ne sont pas évidentes, cependant il paraît possible à ce niveau d’en assurer
une approche correcte et une compréhension réelle par les enfants. Il faut le
plus tôt possible leur donner une véritable formation qui leur permette, d’une
manière adaptée à leur âge, de dégager des concepts mathématiques et qui
leur assure la maîtrise d’une pensée mathématique disponible et féconde. Les
progrès dans la connaissance du développement psychologique de l’enfant
montrent d’ailleurs tout le bénéfice qu’il peut retirer d’un tel enseignement
pour l’ensemble de sa formation.
Ces connaissances mathématiques ainsi construites peu à peu se prolongeront
sans heurt au delà de l’école élémentaire, mais à ce niveau déjà, les
enfants pourront se rendre compte que l’univers mathématique n’est pas
clos sur lui-même et mesurer le pouvoir que leur donne l’outil mathématique
sur l’univers réel.
Depuis 1964, des expériences nombreuses ont été réalisées en particulier
autour des Écoles Normales, dans le cadre des recherches organisées par l’Institut Pédagogique National, elles permettent dès maintenant d’élaborer un
programme adapté à un enseignement rénové. Mais la mise en œuvre généralisée
d’un tel enseignement suppose que tous les maîtres aient pu bénéficier
d’une préparation appropriée et demande un certain délai. Aussi la sous-commission
est amenée à proposer des mesures provisoires immédiatement applicables.
Elles consisteraient à alléger le programme actuel de l’enseignement
élémentaire et à adopter une nouvelle rédaction de celui-ci. La sous-commission
a proposé cette rédaction à la commission pleinière, qui l’a acceptée ;
elle n’introduit à dessein aucune terminologie nouvelle.
D’autre part, les instructions actuelles (de 1945) devenant par le fait
même caduques, les maîtres pourraient s’inspirer avantageusement, surtout
pour les questions dont le point de vue a été rénové, des « commentaires »
présentés également par la sous-commission. Dans la rédaction du programme,
les trois niveaux, CP, CE (en deux ans) CM (en deux ans) sont conservés.
Pour chacun de ces niveaux, les notions numériques qui constituent
l’essentiel du programme sont présentées dans le paragraphe1. Les paragraphes
suivants proposent des thèmes d’activités plus divers : le paragraphe 2
concerne l’observation de l’espace et des objets « géométriques » ; le paragraphe
3 envisage la pratique des mesures dans une perspective expérimentale.
La matière de ces activités sera donc largement empruntée aux « disciplines
d’éveil )J.
Les activités désignées jusqu’alors sous le vocable de « calcul » ne constituent
qu’une partie de l’activité mathématique, il convient de désigner désormais
la matière du programme sous le terme “mathématique” .
La sous-commission espère que la nouvelle rédaction du programme et
l’allègement substantiel de celui-ci inviteront les maîtres à réfléchir sur le
contenu mathématique de leur enseignement. Ils y seront aidés par les commentaires,
ceux-ci ont été particulièrement détaillés à propos des questions dont
la présentation peut être avantageusement renouvelée ; pour faciliter leur étude,
ils ont été rédigés non pas par niveau, mais par thème du programme.
- 2. Programme (1945 modifié 1969)
- Cours préparatoire
Notion de nombre naturel. Nommer et écrire des nombres.
Comparer deux nombres. Somme de deux nombres. - Cours élémentaires 1re et 2e années
- 1) Les nombres naturels : nom et écriture.
Somme et différence de deux nombres ; pratique de l’addition et de la
soustraction.
Produit de deux nombres ; pratique de la multiplication.
Quotient exact de deux nombres ; division avec reste ; pratique de la division par un nombre d’un chiffre.
Calcul mental. - 2) Exercices d’observation et travaux sur des objets géométriques.
Tracés, découpages, pliages.
Cube, carré, rectangle, triangle.
Quadrillages. - 3) Mesures : exercices pratiques.
Lecture de l’heure. Usage du calendrier.
- 1) Les nombres naturels : nom et écriture.
- Cours moyen 1re et 2e années
- 1) Éléments de mathématique.
Nombres naturels et décimaux : nom et écriture.
Multiplication et division par la, 100, 1000 .....
Opérations et leurs propriétés ; suite d’opérations ; pratique des opérations ;
calcul mental.
Divisibilité des nombres naturels par 2, 5, 9.
Fractions considérées comme opérateurs. Produit de deux fractions.
Exemples de relations numériques. Proportionnalité. - 2) Exercices d’observation et travaux sur des objets géométriques.
bande, parallélogramme (et ses· cas particuliers), triangle ;
disque, cercle ;
parallélépipède. - 3) Mesures : exercices pratiques ;
longueur, aire, volume ;
temps, masse ;
expressions d’un résultat avec une unité convenablement choisie. Ordre
de grandeur. Encadrements.
- 1) Éléments de mathématique.
- Cours préparatoire
- 3. Commentaires
- 1. Nombres et opérations.
L’ordre dans lequel les rubriques sont énumérées ci-dessous n’est pas nécessairement
l’ordre chronologique de leur présentation dans les classes. Il appartiendra
à chaque maître d’organiser sa progression selon les possibilités des élèves et ses
préférences personnelles.- 1.Notion de nombre naturel
- 2. Nommer et écrire les nombres
- 3. Comparer deux nombres
- 4. Opérations - Propriétés - Pratique
- 5. Décimaux
- 6. Relations numériques : tableaux de nombres
- 9. Fractions.
- 1.1. Notion de nombre naturel
Le programme du C.P. a été réduit à :
l’élaboration du concept de nombre naturel ;
une initiation à la numération ;
l’apprentissage de l’addition des nombres naturels.
C’est en manipulant de multiples collections d’objets que les enfants
élaborent peu à peu la notion de nombre naturel. Il est essentiel de bien comprendre
que le nombre naturel n’est ni un objet, ni une propriété attachée
à des objets, mais une propriété attachée à des collections.
A l’École Maternelle, pour dégager la notion de couleur, qui est une
propriété d’objets, on pratique des exercices de classement portant sur des
objets variés dont la forme, la matière, la taille ... sont différentes, afin de
répartir ces objets selon leur couleur.
Dé telles activités devront être reprises dans les premières semaines
du Cours Préparatoire (les propriétés n’étant pas nécessairement des propriétés
d’ordre sensoriel).
La notion de nombre naturel comme propriété d’une collection apparaîtra
dans la mesure où l’on pourra établir une mise en correspondance
terme à terme entre collections. Cette correspondance est indépendante de
la nature et de la disposition des objets qui constituent les collections.
Exemples
1. Si on peut mettre en correspondance un à un les enfants de la classe
et les porte-manteaux, on conclut qu’il y a autant d’enfants que de portemanteaux
et autant de portemanteaux que d’enfants.
2. Deux enfants étalent sur leur table le contenu de leur trousse. Si
l’on peut mettre en correspondance un à un les objets d’une trousse et ceux
de l’autre (sans s’occuper de leur nature ni de leur disposition), on peut
conclure qu’il y a autant d’objets dans l’une des trousses que dans l’autre.
C’est quand on aura multiplié ces exercices que les enfants comprendront
que le nombre est une propriété qui s’attache à des collections, et ceci par
une démarche analogue à celle qui leur avait permis de comprendre à l’École
Maternelle que la couleur, par exemple, est une propriété qui s’attache à des
objets.
L’emploi systématique de la correspondance terme à terme permettra
de classer des collections et d’attribuer à chaque classe un nombre : ainsi,
la classe de toutes les collections qui ont autant d’objets que l’on a de doigts
dans une main définit le nombre naturel « cinq ». Cinq doigts, cinq enfants,
cinq fruits, etc... ne sont pas des nombres : le nombre cinq est une propriété
commune à l’ensemble des doigts d’une main, à un groupe d’enfants, au
contenu d’une coupe de fruits.
Dans le premier exemple, si la correspondance un à un est impossible,
il y a plus de portemanteaux que d’enfants ou plus d’enfants que de
manteaux. On insistera sur le sens des expressions : autant que, plus que, moins que. - 1.2. Nommer et écrire les nombres
Chaque nombre naturel peut être représenté par un signe. Nommer et
écrire un nombre naturel avec un nombre limité de signes constitue ce que
l’on désigne sous le terme « numération ».
L’activité de base est le groupement des objets d’une collection selon
un certain mode. Une telle activité s’impose d’elle-même dès que les collections
ont « beaucoup » d’objets.
Exemples de jeux de groupements préalables à la numération :
1er jeu : Dans une classe de vingt-sept enfants, on groupe les enfants quatre
par quatre. Cela fait :
six groupes de quatre enfants,
trois enfants non groupés.
2e jeu : On répète l’opération de groupements avec les groupes de quatre
enfants, cela fait :
un "grand groupe" formé de quatre groupes de quatre enfants chacun,
deux « groupes » de quatre enfants,
trois enfants non groupés.
Ces résultats peuvent, si on le désire, être consignés dans un tableau :

On pourra faire des exercices analogues en groupant par trois, par cinq,
par dix...
Si l’on choisit de grouper par dix, on retrouve la numération usuelle
(décimale) : les « groupes » sont des dizaines, les « grands groupes » des centaines
etc...
Ainsi, dans l’exemple précédent, le tableau devient :
C’est à la numération décimale seule que correspond la numération orale
habituelle : dans cet exemple 27 est lu vingt sept.
Au cours de ces exercices d’écriture, on rencontre fréquemment le zéro (0)
comme signe pour représenter la propriété d’une collection sans objet.
Il paraît raisonnable de ne pas dépasser cent au cours préparatoire et
dix mille au cours élémentaire. - 1.3. Comparer deux nombres
Emploi du signe « = »
Au cours de la scolarité, on verra qu’un nombre peut s’exprimer de différentes
façons. Exemple : 6 ; 2 X 3 ; 4 + 2 ; 8 - 2 ; 24/4 ; 24 : 4 sont des expressions
du même nombre.
Cela donne le droit d’écrire
6=6
6=2X3
2 X 3 = 4 + 2 etc...
Emploi des signes \( \neq ; > ; <\)
On utilisera avec profit ces signes dès l’école élémentaire :
\(3 \neq 4\)
3<4
\(2+3\neq4+2\)
3X2>5-1
18/3 < 7 X 2 etc... - 1.4. Opérations : propriétés, pratique
L’étude des nombres naturels comprend celle des deux opérations élémentaires
: l’addition, la multiplication, qui donnent à l’ensemble de ces
nombres sa structure algébrique propre.
Parmi les opérations qui se rattachent aux précédentes, on étudie également
la soustraction, la division exacte et la division euclidienne (avec reste
pouvant être différent de zéro).
« Sens » de ces opérations
Il faut que les enfants comprennent que l’addition, la multiplication,
etc... ne portent que sur des nombres.
Addition-Soustraction
Exemple 1 : On réunit dans une corbeille 8 pommes et 7 pommes ... Le
nombre de toutes les pommes est alors (8 + 7).
(8 + 7) est une première expression immédiate de la somme des nombres
8 et 7. Elle utilise un signe particulier, le signe « + » (plus). Les parenthèses
soulignent qu’il s’agit de l’expression d’UN nombre ; à ce point de vue il est
utile d’en faire usage dès l’école élémentaire.
L’addition est l’opération qui associe aux nombres 8 et 7 leur somme
(8 + 7).
Habituellement on cherche à désigner ce nombre (8 + 7) sans utiliser
le signe +. Le groupement des objets selon la numération décimale conduit
à écrire ce nombre 15 (quinze).
Alors (8 + 7) et 15 sont deux expressions d’un même nombre, ce qui
justifie l’égalité (8 + 7) = 15 que l’on écrit plus simplement :
8+7=15
c’est par abus de langage qu’on a pu écrire des expressions telles que
8 pommes + 7 pommes = 15 pommes
qui n’appartiennent en fait, ni au langage mathématique ni au langage usuel.
On n’écrit donc pas 8 pommes + 7 pommes = 15 pommes.
On écrit : le nombre de pommes est (8 + 7) :
8+7=15
ce qui permet de conclure en langage courant « la corbeille contient 15 pommes ».
Au lieu d’écrire (8 + 7) on peut choisir d’écrire (7 + 8).
Aux couples (8 ; 7) et (7 ; 8) l’addition associe le même nombre (elle est
commutative).
Remarquons que : 8 + 0 = 8, 0 + 8 = 8 ; 4 + 0 = 4 ; 0 + 0 = 0, etc...
Exemple 2 : Parmi 15 fruits, 8 fruits sont des pommes ... Le nombre des
fruits qui ne sont pas des pommes est alors celui qui complète l’égalité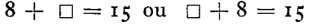
On cherche parmi les nombres (8 + 0), (8 + 1), ... celui qui est égal à
15. Le nombre cherché est (8 + 7). Le nombre qui doit remplacer le carré
est donc 7.
On peut aussi désigner directement le nombre par l’expression (15 - 8)
qui utilise le signe « - » (moins).
Ceci conduit à écrire : 15 - 8 =7.
La soustraction est l’opération qui associe aux nombres 15 et 8 leur
différence (15 - 8) (ou encore 7).
Au Cours Préparatoire, il suffit que les enfants sachent utiliser correctement
l’addition. La soustraction sera introduite au Cours Élémentaire.
Multiplication
Exemple : On réunit 7 collections qui comprennent 8 objets chacun.
Le nombre de tous les objets est alors :
(8 + 8 + 8 + 8 + 8 + 8 + 8) ou (7 + 7 + 7 + 7 + 7 + 7 + 7 + 7)
Par convention, ce nombre peut être écrit indifféremment :
(8 X 7) ou (7 X 8).
C’est le produit des nombres 8 .et 7.
Dans les expressions précédentes,le signe « X » se lit « multiplié par »
Les deux expressions (8 X 7) et (7 X 8) désignent le nombre de tous
les objets. On constate que ce nombre est 56 donc : (8 X 7) = 56 ou (7 X 8)
= 56 ce que l’on écrit plus simplement 8 X 7 = 56 ou 7 X 8 = 56.
La multiplication est l’opération qui associe à deux nombres leur produit.
Ainsi, aux couples (8 ; 7) et (7 ; 8) la multiplication fait correspondre le
même nombre
8 X 7 = 7 X 8 (la multiplication est commutative).
Remarquons que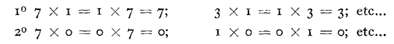
Tables
Aux tables traditionnelles, on préfèrera des tables de Pythagore construites
par les élèves avec des nombres divers (sans oublier les lignes et colonnes
qui comprennent 0 et 1).
Exemples :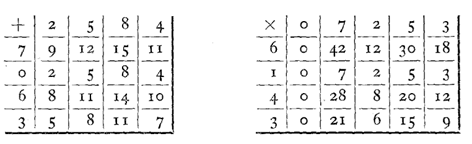
La construction de telles tables facilite l’apprentissage et la mémorisation
de sommes et de produits indispensables au calcul. On construira notamment
les tables d’addition et de multiplication dans lesquelles les nombres placés
en ligne et colonne sont ordonnés de 0 à 9.
Division exacte
Exemple : On a dénombré 56 objets en réunissant 7 collections qui comprenaient
chacune le même nombre d’objets.
Il est naturel de désigner ce nombre par un signe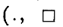
ou une lettre
quelconque) et d’écrire une égalité entre les deux expressions du nombre
de tous les objets.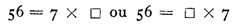
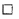
représente un nombre que l’on peut désigner directement par l’expression
(56 : 7) ou (56/7)
La division est l’opération qui associe aux nombres 56 et 7 leur quotient
exact (56 : 7).
Ce nombre s’écrit 8 d’où l’égalité (56 : 7) =8 que l’on écrit plus simplement
56 : 7 = 8.
Cet exemple montre que la division exacte peut intervenir à propos d’un
partage d’objets (lorsque les parts ont le même nombre). Mais son véritable
sens découle de sa liaison avec la multiplication ; les égalités :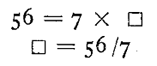
disent la même chose.
Remarque :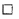
représente un nombre naturel parce que 56 est un multiple
de 7.
D’une façon générale, le quotient exact de deux nombres naturels n’existe
que si le premier est multiple du deuxième.
Il ne faut donc désigner un quotient à l’aide d’un des signes « :» ou
« / » que lorsque l’on sait que ce quotient existe.
Division euclidienne (division avec reste, ce reste pouvant être nul).
Exemple : On veut distribuer équitablement 17 cerises entre 3 enfants.
Existe-t-il un nombre x de cerises tel que chaque enfant reçoive x cerises et
qu’il n’en reste plus ?
Formons la suite des produits (3 X1) ; (3 X 2) ; (3 X 3) etc ... Aucun
de ces nombres n’est égal à 17 donc il est impossible de servir équitablement
les enfants en utilisant toutes les cerises
On constate que :
(3 X 5) < 17 < (3 X 6)
et aussi que 17 =(3 X 5) + 2
Cette dernière égalité montre que le plus grand nombre de cerises
l’on peut donner à chaque enfant est 5 ; 2 cerises ne sont pas, distribuées.
La division euclidienne de 17 par 3 fait correspondre au couple de nombres
(17 ; 3) le couple (5 ; 2).
5 est le quotient entier de 17 par 3 ;
2 est le reste de la division euclidienne de 17 par 3.
Remarque : Il est incorrect d’écrire 17 : 3 = 5 car 17 : 3 devrait représenter
un quotient exact, or \(5 X 3\neq 17\)
Par convention, on peut désigner le quotient entier de 17par 3 par l’expression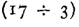
ce qui donne le droit d’écrire
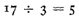
Suites d’opérations :
Additions successives - Somme de trois nombres.
Exemple : A partir des nombres 8, 7, 5, on calcule :
(8 + 7) c’est-à-dire 15,
puis (8 +7) + 5) c’est-à-dire (15 + 5).
On constate que ce nombre peut être obtenu par un autre mode de calcul,
sans modifier l’ordre des nombres donnés (8, 7, 5)
On peut, en effet, calculer (7 + 5) c’est-à-dire 12, puis (8 + (7 + 5))
c’est-à-dire (8 + 12).
La somme des trois nombres 8, 7, 5 s’écrit (8 + 7 + 5). On peut la
calculer de l’une ou l’autre des deux manières précédentes.
(Cet exemple illustre une propriété de l’addition : l’associativité).
Multiplications successives : Produit de trois nombres
Exemple : On calcule (5 X 6) puis [5 X 6) X 4) c’est-à-dire (30 X 4)
ou bien (6 X 4) puis (5 X (6 X 4] c’est-à-dire (5 X 24).
Les deux expressions ainsi écrites désignent en fait le même nombre
Ceci peut être constaté en revenant à des collections d’objets.
Le produit des trois nombres 5, 6, 4 s’écrit (5 X 6 X 4). On peut le
calculer de l’une ou l’autre des deux manières indiquées.
(Cet exemple illustre le fait que la multiplication est associative).
Addition et multiplication
Exemple : Calculer (2 + 5) puis (2 + 5) X 3) c’est-à-dire (7 X 3)
Peut-on obtenir le même résultat d’une autre façon ?
On constate que ce nombre est le même que la somme
(2 X 3) + (5 X 3) c’est-à-dire (6 + 15)·
(Cet exemple illustre une nouvelle propriété de ces opérations : la multiplication
est distributive par rapport à l’addition).
Le fait de pouvoir désigner et calculer un nombre de plusieurs façons
différentes, est donc une conséquence des propriétés essentielles de l’addition
et de la multiplication que nous venons de signaler au passage :
commutativité et associativité de l’addition et de la multiplication, distributivité
de la multiplication par rapport à l’addition.
Il n’est nullement question de vouloir nommer de telles propriétés au
niveau élémentaire. Mais il est important de faire en sorte que les enfants les
utilisent de façon naturelle et familière, parce qu’elles sont à l’origine de tous
les modes de calcul : calcul mental et techniques usuelles.
Techniques opératoires
Il est indispensable que les techniques usuelles concernant les opérations
soient parfaitement connues. Elles ne seront pas apprises par les enfants de
façon purement mécanique, mais découvertes par eux-mêmes comme synthèse
d’expériences suffisamment variées et nombreuses. - 1.5. Nombres décimaux
Les nombres décimaux sont introduits au cours moyen ; à ce niveau,
les enfants savent écrire et nommer les nombres naturels à partir de groupements
d’objets d’une collection (cf. § 1.2.).
Au lieu d’écrire le nombre de tous les objets, on peut chercher à écrire
le nombre des groupements d’une certaine espèce.
Exemple 1 : le nombre d’habitants de la France est cinquante millions. Si
l’on imagine une répartition des Français en groupements comprenant chacun
un million d’habitants, le nombre de ces groupements s’écrit 50. Il exprime
la population de la France, le million étant choisi comme unité.
Si les groupements choisis comprennent cent habitants, la population
s’exprime par le nombre qui s’écrit : 500 000.
Si les groupements ne comprennent qu’un seul habitant, la population
s’exprime par le nombre qui s’écrit : 50 000 000.
Exemple 2. La population de l’agglomération de Romorantin compte 10 850 habitants.
Le millier étant choisi comme unité, la population s’exprime par le
nombre décimal 10,850.
La virgule est utilisée pour repérer le rang du groupement choisi comme
unité.
D’autres exemples pourront être trouvés à l’occasion d’exercices de mesure
utilisant le système métrique.
On remarquera qu’à tout nombre naturel exprimant une mesure on peut
associer, par un changement d’unité convenable un nombre décimal et qu’à
tout nombre décimal on peut associer, par un changement d’unité, un nombre
naturel (et ce de diverses façons).
Les opérations sur les décimaux reviennent donc aux opérations de même
nom sur les nombres naturels associés.
Relations numériques : tableaux de nombres
Exemple : 1. On choisit une liste de nombres
3, 9, 14, 25, 17
A chacun de ces nombres on additionne 4.
On construit ainsi une deuxième liste de nombres déduite de la première
7, 13, 18, 29, 21
On peut disposer ces deux listes en utilisant un tableau mettant en évidence
la correspondance terme à terme
La consigne « soustraire 4 » fait correspondre à tout nombre de la deuxième
liste un nombre de la première liste.
Cas particulier : « Additionner. 1 -Soustraire 1 »
A chacun des nombres de la première liste, la consigne « additionner 1 »
fait correspondre son successeur dans la suite des nombres naturels (0, l, 2,
3, 4,·· .).
A chacun des nombres de la deuxième liste, la consigne « soustraire 1 »
fait correspondre son prédécesseur dans la suite des nombres naturels.
Pour construire des tableaux de nombres, on peut utiliser d’autres
consignes telles que « multiplier par ... » « diviser par .,. » (division exacte
quand elle est possible).
2. Connaissant la consigne qui fait passer de la première à la deuxième
liste, on peut chercher un élément manquant dans l’une ou l’autre de ces
listes, connaissant l’élément correspondant à l’autre :
Remarque : on s’aperçoit qu’aucun nombre ne correspond à 42 (42 n’est
pas multiple de 5).
3. Connaissant un couple d’éléments correspondants, trouver les consignes
de l’un des quatre types précédents (additionner ... ;’ soustraire ... ; multiplier
par ... ; diviser par ...) qui font passer d’une liste à l’autre.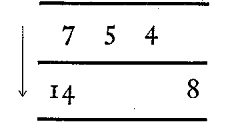
(deux consignes possibles : additionner 7 ; multiplier par 2).
4. Connaissant deux couples correspondants de deux listes, trouver la
consigne de l’un des 4 types précédents qui fait passer d’une ligne à l’autre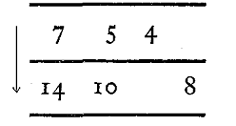
(la seule consigne possible est multiplier par 2).
Lorsque la consigne est « multiplier par » ou « diviser par », les exercices
sur les tableaux de nombres correspondent à l’étude de la proportionnalité.
Dans l’ensemble des problèmes traités au cours moyen, on rencontre les thèmes
suivants : recherche de
prix à payer pour une certaine longueur de ruban, connaissant le
prix pour une longueur déterminée de ce ruban ;
poids correspondant à un certain volume de matière homogène
sachant le poids pour un volume connu de cette matière ;
prix d’un terrain connaissant le prix de l’hectare ;
distance parcourue en un temps donné connaissant le temps mis
pour effectuer un trajet déterminé, dans le cas d’un mouvement uniforme ;
pourcentage ;
rendement ;
crédit ;
échelle ;
etc...
Il est essentiel de savoir qu’il s’agit d’un seul et même problème, qu’il
convient d’expliquer en termes nouveaux. D’une façon générale, tous les
problèmes traités au moyen de la « règle de trois » relèvent du modèle mathématique
précédent.
Exemples : 1) Pour une fête, des enfants font des colliers composés tous du
même nombre de perles. Un enfant a utilisé 45 perles
pour faire 3 colliers.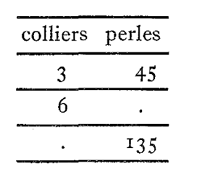
Le tableau ci-contre permet de répondre aux deux questions :
Combien faut-il de perles pour fabriquer 6 colliers ?
Combien de colliers peut-on fabriquer avec 135 perles ?
Il suffit en effet
1° de chercher la consigne qui fait passer de la première à la deuxième
colonne (c’est-à-dire « multiplier par 15 » (la situation étant une situation
« multiplicative », la consigne ne peut être « additionner 42 ll) ;
2° Calculer 6 X 15 ;
3° Calculer 135/15 ;
2) On sait que 5 centimètres sur une carte représentent 10 kilomètres
sur le terrain.
A quelle distance sur le terrain correspond une distance de 18 centimètres
sur la carte ?
A quelle distance correspond sur la carte une distance de 32 kilomètres
sur le terrain ?
Le tableau suivant permet de répondre aux questions
La consigne qui fait passer de 5 à 10 est « multiplier par 2 » ce qui permet
de trouver le correspondant de 18 dans la deuxième ligne soit (18 X 2)
c’est-à-dire 36 et le correspondant dans la première ligne de 32, soit (32/2)
c’est-à-dire 16.
On peut donner maintenant les réponses en langage courant :
18 centimètres sur la carte correspondent à 36 kilomètres sur le terrain,
32 kilomètres sur le terrain sont représentés par 16 centimètres sur la carte.
3) On considère une série de rectangles de même largeur mesurée par
le nombre 4 et de longueurs différentes.
Un quadrillage permet de déterminer les aires de ces rectangles en prenant
comme unité d’aire le carré de côté 1 (cf. 3, mesure).
Nous pouvons construire le tableau de correspondance entre la longueur
et l’aire de ces rectangles De façon générale si la longueur, l’unité
étant choisie comme il est dit plus haut, est x, l’aire (l’unité étant déterminée
comme plus haut) est 4 x.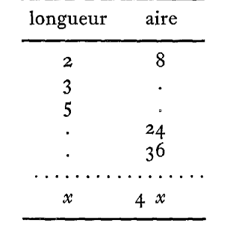
Nous pouvons constater sur les tableaux précédents les propriétés suivantes :
1°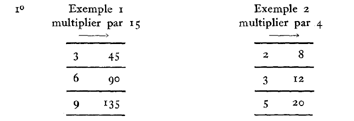
Remarquons que :
dans le 1er tableau 3 + 6 = 9 ; 45 + 90 = 135
dans le 2e tableau 2 + 3 = 5 ; 8 + 12 = 20.
De façon générale, à la somme de deux nombres de la première colonne
correspond la somme des nombres associés de la deuxième colonne.
Ceci peut être représenté par le tableau :
Au produit par y d’un nombre quelconque m de la première colonne correspond
le produit par y du nombre de la deuxième colonne associé à m.
Suites d’additions et de soustractions
Exemple 1
- 1. Nombres et opérations.
| 4 | 9 | 11 | ||
| 7 | 12 | 14 | ||
| 9 | 14 | 16 | ||
| --->add. 5 | --->add. 2 |
On peut passer directement de la première à la troisième colonne en
additionnant 7 à chacun des nombres de la première colonne.Suites d’additions et de soustractions.
Exemple 2
| 8 | 6 | 3 | ||
| 5 | 3 | 0 | ||
| 4 | 2 | |||
| 2 | ||||
| --->soustr. 2 | --->soustr. 3 |
On peut passer directement de la première à la troisième colonne en
soustrayant 5 à chacun des nombres de la première colonne (ce qui est possible
si ces nombres sont égaux ou supérieurs à 5)
(5 = 2 + 3)
Exemple 3
| 5 | 8 | 4 | ||
| 8 | 11 | 7 | ||
| 2 | 5 | 1 | ||
| --->add. 3 | --->soustr. 4 |
On peut passer directement de la première à la troisième colonne en soustrayant
1.
(1 = 4 - 3)
Exemple 4
| 5 | 9 | 6 | ||
| 8 | 12 | 9 | ||
| 2 | 6 | 3 | ||
| --->add. 4 | --->soustr. 3 |
On peut passer directement de la première colonne en additionnant 1
à chacun des nombres de la première colonne.
(1=4-3)
Suites de multiplications et de divisions exactes
Exemple 1
| 3 | 6 | 18 | ||
| 5 | 10 | 30 | ||
| 4 | 8 | 24 | ||
| --->mult. par 2 | --->mult. par 3 |
On peut passer directement de la première à la troisième colonne en multipliant
par 6.
Remarquons que les résultats de la troisième colonne auraient été les
mêmes si on avait d’abord multiplié par 3 puis si on avait multiplié le résultat
par 2
Exemple 2
| 36 | 12 | 3 | ||
| 24 | 8 | 2 | ||
| 48 | 16 | 4 | ||
| --->div. par 3 | --->div. par 4 |
On peut passer directement de la première à la troisième colonne en
divisant par 12.
Remarquons que les résultats de la troisième colonne auraient été les
mêmes si on avait d’abord divisé par 4 puis si on avait divisé le résultat par 3·
Exemple 3
| 1 | 10 | 5 | ||
| 7 | 70 | 35 | ||
| 0 | 0 | 0 | ||
| 4 | 40 | 20 | ||
| --->mult. par 10 | --->div. par 2 |
On peut passer directement de la première à la troisième colonne en
multipliant par 5 (10 est multiple de 2).
Exemple 4
| 4 | 12 | 1 | ||
| 12 | 36 | 3 | ||
| 24 | 72 | 6 | ||
| 16 | 48 | 4 | ||
| --->mult. par 3 | --->div. par 12 |
On peut passer directement de la première à la troisième colonne en
divisant par 4 (12 est multiple de 3).
Exemple 5
| 35 | 210 | 21 | ||
| 5 | 30 | 3 | ||
| 15 | 90 | 9 | ||
| 20 | 120 | 12 | ||
| --->mult. par 6 | --->div. par 10 |
Il n’est pas possible de passer directement de la première à la dernière
colonne en multipliant ou divisant par un nombre naturel :
6 n’est pas multiplie de 10 ;
10 n’est pas multiple de 6.
Fractions comme opérateurs
Par définition du symbole (6/10), dans l’exemple 5, on peut passer de la
première à la troisième colonne en multipliant chaque nombre par (6/10)
On dit que (6/10) est une fraction.
D’une façon générale, x et y désignant des nombres naturels, \(y \neq 0\)
multiplier par (x /y) revient à multiplier par x puis diviser le résultat par y.
Remarquons que [multiplier par (2/10)] est équivalent à [multiplier par 0,2]

On constate qu’à partir de la même première colonne, on obtient la même
troisième colonne
en multipliant par 7 puis en divisant le résultat par 4 ou
en divisant par 4 puis en multipliant le résultat par 7.
Dans les deux cas, on a multiplié par (7/4).
Remarquons que les calculs sont plus faciles dans l’exemple 6.2.
Opérateurs équivalents
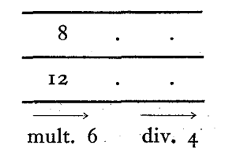
Exemple 7
Ce tableau peut être décomposé de la façon suivante
| 8 | ||||||
| 12 | ||||||
| --->mult. par 3 | --->mult.2 | --->div. 2 | --->div. 2 |
multiplier par 2 puis diviser par 2 est équivalent à mult (2/2), c’est-à-dire
(mult. 1).
Le tableau se réduit à
| 8 | |||
| 12 | |||
| --->mult. par 3 | --->div. 2 |
mult. (6/4) est équivalent à mult. (3/2).
Exemple 8
| 18 | |||
| 12 | |||
| --->mult. par 2/3 | --->mult. par 5/4 |
Par définition :
mult (2/3) est équivalent à la suite mult. 2, div. 3 ;
mult (S /4) est équivalent à la suite mult. 5, div. 4 ;
donc la suite mult. (2/3), mult. (5 /4) est équivalent à la suite mult. 2, div. 3,
mult. 5, div. 4.
On sait aussi que la suite div. 3, mult. 5 est équivalente à la
suite mult. 5, div. 3. La suite mult. (2/3), mult. (5/4) est donc équivalente
à la suite mult. 2, mult. 5, div. 3, div. 4 ; ce qui donne, en composant la suite,
mult. 10, div. 12 ou mult. (10/12).
Donc la suite mult. (2/3), mult. (5 /4) est équivalent à mult. (10 /12).
On peut constater que mult. (10/12) est équivalent à mult. (5/6) ;
donc la suite mult. (2/3), mult. (5/4) est équivalent à mult. (S/6).
Exemple 9
La suite mult. (2/3), mult. (3/2) est équivalent à la suite mult. 2, div. 3,
mult. 3, div. 2 ; div. 3, mult. 3 est une suite équivalente à mult. 1.
La suite précédente se réduit donc à la suite mult. 2, div. 2, elle-même
équivalent à mult. 1.
donc la suite mult. (2/3), mult. (3/2) est équivalente à mult. 1.
Dans le langage courant, on trouve des expressions telles que un quart
d’heure, un demi-litre, avoir parcouru les trois quarts du chemin ....L’emploi
de ces expressions qui utilisent le vocabulaire des fractions donne lieu à des
calculs numériques où l’on retrouve les fractions comme opérateurs sur les
nombres entiers naturels.
-* 2. Exercices d’observation et travaux sur des objets géométriques
Ces exercices trouvent naturellement leur place dans les activités d’éveil.
L’espace physique et les objets qui le peuplent fournissent une matière sur
laquelle la pensée mathématique a bien des occasions de s’exercer. Ces exercices
doivent, en même temps aider l’enfant à s’adapter à ce milieu. Ils font
appel, non seulement à l’observation mais aussi à l’activité manuelle qui
soutient, complète l’observation et l’étude des situations et des choses. L’enfant
doit acquérir le goût de travaux manuels : tracer, dessiner, plier, découper
pour construire : l’emploi des instruments (règle, équerre, compas ...) pour
la réalisation de ces constructions développera l’habileté et le soin.
On se devra de proposer aux enfants des thèmes et des buts d’activité
à leur mesure et conformes à leur intérêt.
Il y aura souvent avantage à réaliser ces exercices en équipes.
Les démarches mathématiques porteront, comme dans le domaine
numérique sur la découverte de propriétés, les classements selon telle ou telle
propriété, l’étude de relations sur un objet ou entre des objets. On reconnaît :
que deux lignes droites sont perpendiculaires ou forment un angle droit
par un pliage convenable ou à l’aide de l’équerre ;
que deux lignes droites sont parallèles à l’aide de la règle et de l’équerre ;
qu’un polygone découpé dans du carton épais et rigide est convexe par
exemple en l’entourant d’un élastique et constatant que cet élastique est en
contact avec tous les sommets.
Pour un polygone, on peut s’intéresser aux propriétés suivantes : convexité,
nombre de côtés, nombre de sommets, longueur de côtés, existence de
côtés perpendiculaires, existence de côtés parallèles, etc...
Les enfants ayant construit différents polygones, ils pourront les classer
selon l’une ou l’autre de ces propriétés : ainsi, s’il s’agit de quadrilatères
ils distingueront par exemple, les parallélogrammes et parmi ceux-ci les rectangles,
les losanges. Ils découvriront ainsi que les carrés sont les quadrilatères
qui ont la propriété d’être à la fois des rectangles et des losanges.
Pour un polyèdre (tétraèdre, cube, parallélépipède, prisme, dodécaèdre
etc...) on pourra s’intéresser à la nature des faces, à leur nombre ainsi qu’à
celui des sommets et des arêtes etc... Dans ce but, les élèves à l’occasion du
travail manuel construiront de tels objets géométriques, en carton par exemple.
- 3. Mesures : exercices pratiques
A l’école primaire, l’idée de mesure sera toujours intimement liée à
la pratique, à l’activité manuelle, à l’expérience, à l’étude du milieu.
Le rôle du maître consistera à offrir aux enfants un vaste champ d’expériences les amenant à ressentir le besoin de mesurer : longueurs à comparer,
charges à évaluer, temps à estimer.
Pour exprimer une mesure, il faut choisir une unité : la mesure est alors
un nombre.
Jusqu’au cours élémentaire, on ne connaît que les nombres naturels ;
à partir du cours moyen, on peut utiliser les nombres décimaux. Une unité
de mesure étant choisie, on pourra trouver un encadrement d’une mesure.
Les unités seront d’abord celles que proposeront les enfants. La nécessité
de la communication des résultats des mesures amènera à choisir, pour
tous les élèves de la classe, pour tous les groupes d’enfants travaillant en équipe,
la même unité. On arrivera ainsi .peu à peu à l’utilisation des unités légales.
Une mesure étant un nombre, les opérations sur les nombres seront
naturellement utilisées dans les exercices sur les mesures.
Exemples :
1) On met bout à bout deux règles dont les longueurs, l’unité étant le centimètre, sont 12et 5, pour former une barre.
On n’écrira pas
12 cm + 5 cm = 17 cm ;
mais : le centimètre étant l’unité, la longueur de la barre est (12 + 5)
12 + 5 = 17 ;
le centimètre étant l’unité, la longueur de la barre est 17 ;
ou, en langage courant, la longueur de la barre est 17 centimètres.
2) Aire (mesure de la surface) d’un rectangle.
On construit un rectangle dont les côtés ont pour longueur 5 et 3 (l’unité
étant le centimètre).
Le rectangle se décompose naturellement en (5 X 3) carrés qui ont tous
1 centimètre de côté. Si on choisit un de ces carrés (que l’on appelle centimètre
carré) comme unité d’aire, l’aire du rectangle est (5X 3)
5 X 3 = 15
Le centimètre carré étant l’unité, l’aire du rectangle est 15 ou, en langage
courant, l’aire du rectangle est 15 centimètres carrés.
Annexes
N.D.L.R. - En annexe au texte précédent, il nous paraît intéressant de présenter :
ANNEXE 1. Projet de programme adopté par la commission « Recherche et Réforme »
de l’A.P.M.E.P. à partir d’un projet élaboré par le Service de la Recherche Pédagogique
de l’Institut Pédagogique National. Il nous paraît indispensable de faire connaître à
tous ceux qui s’engagent ou s’engageront dans la « première étape » les perspectives ouvertes
par celle-ci.
Perspectives.
L’enseignement de notions mathématiques au niveau élémentaire a un double
objectif : favoriser une bonne structuration mentale, procurer aux enfants un outil
intellectuel utilisable dans les situations les plus diverses qu’ils rencontreront au
cours de leur existence.
Dans cette perspective l’acquisition de ces notions ne peut être faite par un
enseignement dogmatique. Il est indispensable que les enfants tirent de leur propre
expérience les notions sur lesquelles ils pourront bâtir peu à peu des structures
mathématiques cohérentes.
A chaque étape, la pratique d’activités convenablement choisies conduit à
la formation de l’esprit et à la découverte de techniques. Cette découverte résulte
de la compréhension et de l’utilisation préalables des notions mathématiques sous-jacentes.
En particulier, des jeux dont les règles sont, soit proposées par le maître,
soit inventées par les enfants, constituent un moyen efficace d’introduire ces notions
mathématiques.
A tous les niveaux, les enfants découvrent et utilisent diverses représentations
pour :
décrire des situations ;
organiser des informations puisées dans le contexte de la vie scolaire,
familiale, sociale (en particulier des « « matériaux » peuvent être trouvés dans l’étude
de la langue et dans les matières d’éveil).
1. Rubriques sur lesquelles
porteront les activités mathématiques
pratiquées au
niveau élémentaire.
| Ces notions ne peuvent être raisonnablement explicitées avant le : | |
| 1. Logique liaison avec un travail sur des ensembles |
C.P - et, non C.E. - ou C.M. - « si .. alors » - « tout » - « pas tout » « rien » - « pas rien » |
| 2. Relations | C.P. travail sur des couples C.E. partitions composition de relations C.M. applications- ordre, équivalence |
| 3. - Notion de cardinal | C.P.
Activités pré-numériques correspondances terme à terme autant que, plus que, moins que (en utilisant les correspondances terme codage | - 4. Codage de cardinaux : numération.
Codage d’ordinaux (numérotation). |
C.P.
Groupements suivant certaines bases (3, 4, 5, 2 ....) Notion d’échange Codage numérique du résultat de groupements et d’échanges décodage comparaison de cardinaux en utilisant des codes. CE Changement de base CM ordre sur les codes de cardinaux jeux utilisant des processus récursifs introduction de la notation exponentielle numérotation |
5·Opérations sur les cardinaux
(en liaison avec les opérations
sur les ensembles) Techniques opératoires (comme application de la découverte des propriétés des opérations et de l’utilisation la numération de position). |
C.P :
addition CE : soustraction multiplication CM : division A tous niveaux : calcul mental |
6. - Nombres à virgule | C.M : en utilisant différentes bases de numération opérations sur les nombres à virgule | 7. - Relations numériques. |
C.E.1 - « « machines » à additionner et
soustraire
C.E.2 : « « machines » à multiplier et diviser CE : chaînes de machines réduction de chaînes chaînes équivalentes CM : être multiple de être diviseur de découverte de la notion de nombre premier congruences applications linéaires |
7. - Relations numériques. |
C.E.1 - « « machines » à additionner et
soustraire
C.E.2 : « « machines » à multiplier et diviser CE : chaînes de machines réduction de chaînes chaînes équivalentes CM : être multiple de être diviseur de découverte de la notion de nombre premier congruences applications linéaires |
8. - Algébrisation de situations conduisant à certaines structures mathématiques. |
C.P : activités préparatoires : jeux combinatoires C.E. exemples concrets de structures construites sur des ensembles finis CM : « dictionnaires » (isomorphime ) |
9. - Organisation de l’espace |
C.P :
repérage sur des réseaux topologie-labyrinthes, intérieur, extérieur, ouvert, fermé, frontière à droite de, à gauche de, au-dessous de, au-dessus de, à l’avant de, à l’arrière de C.E : déplacement sur un réseau codage et décodage de déplacements relations d’incidence « « borde », « est adjacent à », « est sur » etc. jeux sur des graphes avec flèches C.M. reproduction d’un dessin d’un réseau sur un autre transformations : symétries, translations, homothéties |
10. - Mesure |
C.E. (fin) : travaux pratiques entrant dans le
cadre des activités d’éveil (conduite
d’une expérience, compte rendu
d’une expérience, étude du milieu) C.M : mesure sur fond de quadrillage |
11. - Représentations |
C.P. : Schématisation de situations par des
diagrammes, ensembles de flèches,
tableaux C.E : Exploitation de schémas C.M. : Arbres |
- 2. Présentation du libellé du programme
- 1°. Dans l’approche d’un concept, il y a différentes étapes telles que :
sensibilisation par des activités diverses ;
familiarisation à l’aide d’exemples et de contre-exemples suffisamment
nombreux ;
représentations diverses et prise de conscience ;
imagination d’autres situations analogues ;
explication éventuelle. - 2° Un concept mathématique étant toujours lié à d’autres concepts, se réfère
à plusieurs rubriques au sein desquelles le travail doit donc être mené simultanément. - 3° Il s’ensuit pour les maîtres l’obligation de suivre le rythme des enfants.
Aussi les étapes ne peuvent-elles être fixées de façon précise pour chaque niveau.
C’est pourquoi le programme présente :- a) Une liste de rubriques dont l’ordre n’est pas significatif, ce qui laisse aux
maîtres une grande liberté dans le choix et la conduite des activités à proposer aux
élèves. - b) Une information à propos de chacune de ces rubriques concernant l’explicitation
éventuelle aux différents niveaux, de qui implique aux niveaux précédents
les étapes préliminaires de sensibilisation, familiarisation, etc.
En effet, l’explicitation prématurée et apportée de l’extérieur peut contrarier
la compréhension.
- a) Une liste de rubriques dont l’ordre n’est pas significatif, ce qui laisse aux
- 1°. Dans l’approche d’un concept, il y a différentes étapes telles que :
ANNEXE 2. Nouveau programme et nouvelle organisation pour la formation des MAITRES
Nous publions ici le texte du rapport adopté par la Commission ministérielle sur
l’Enseignement des mathématiques, le I6 juin I969 :
La formation initiale en mathématique
des maîtres de l’enseignement élémentaire.
- 1. La mathématique comme instrument de culture
La mathématique
en ce qu’elle est un outil de raisonnement,
en ce qu’elle constitue une méthode de pensée et d’action,
grâce au rôle privilégié qu’elle joue dans l’intelligence que nous avons du réel de quelque nature qu’il soit,
est un des éléments essentiels de la culture de l’homme contemporain.
Le bagage intellectuel de chacun doit donc comporter un minimum de notion
fondamentales de mathématique. Par ailleurs, ce bagage ne doit pas consister, si
l’on désire qu’il soit réellement moyen de culture, uniquement en une connaissance
formelle de certaines structures mathématiques de base, il doit permettre de comprendre le rôle particulier joué par les mathématiques dans l’appréhension du monde
dans lequel nous vivons et la maîtrise d’un certain nombre de ses phénomènes. Dans
cette perspective, il est nécessaire d’abord de mathématiser des situations réelles.
De leur comparaison se dégagera la notion de structures isomorphes puis de structure
abstraite.
Ceci justifie déjà, pour tout futur maître de l’enseignement élémentaire,la
nécessité d’une solide formation mathématique au niveau de l’Université : celui qui
a une responsabilité dans la formation de l’esprit des enfants doit, plus que tout
autre, disposer pour lui-même de ce bagage minimum sans lequel il serait un sous-développé
intellectuel dans le monde de demain. - 2. La mathématique dans la formation professionnelle du futur
maître
Dans le cadre de la réforme de l’enseignement des mathématiques, une importante mutation de l’enseignement au niveau élémentaire est nécessaire. Cette nécessité s’impose tant sur le plan des contenus que sur le plan des méthodes : les expériences entreprises depuis 5 ans montrent que l’enseignement élémentaire prend
toute sa valeur de formation de l’esprit, donnant à chacun - quel que soit le contexte
socio-cu1turel dans lequel il vit - son développement optimum
lorsqu’il permet de prendre conscience des possibilités de création, de maîtrise
des situations proposées ;
lorsqu’il donne l’occasion de constater que plusieurs situations diverses en apparence, relèvent en fait d’un même modèle, ont même structure ;
lorsqu’il donne un moyen d’organiser les informations éparses et d’en tire
parti.
Par leur nature même, les mathématiques sont un moyen de choix pour atteindre
de tels objectifs. Mais il est bien évident que ces objectifs ne seront réalisés qu’à
la seule condition d’utiliser des méthodes
suscitant l’initiative des élèves ;
développant leurs capacités d’invention ;
acceptant des solutions diverses (même si elles ne sont pas celles qui apparaissent
les plus simples à l’adulte) ;
permettant à chacun par un travail individualisé de progresser au rythme qui
lui est propre.
Or, ce changement de méthode (faire découvrir et non transmettre des connaissances
d’une manière pré-organisée) nécessite pour le maître de dominer de façon
très sûre la matière qu’il enseigne : il n’est pas possible de tirer parti d’une suggestion
d’un élève si l’on ne voit pas de façon immédiate les prolongements possibles de cette
suggestion. Le maître ne doit donc pas recevoir seulement une formation lui donnant
la possession des bases mathématiques des notions qu’il doit faire acquérir à ses
élèves mais aussi une formation telle qu’il domine les prolongements de ces notions
(c’est ainsi que dans le programme proposé certaines notions telles que celle de produit
scalaire, de continuité et de limites pourraient paraître inutiles dans la perspective
où l’on considèrerait qu’il suffit que le maître connaisse ce qu’il doit enseigner).
Un maître n’aura de liberté vis-à-vis de ce qu’il enseigne et en conséquence ne
pourra accorder une autonomie à ses élèves qu’à la condition de dominer la matière
enseignée. Cela nécessite en particulier une réflexion sur la mathématique elle-même
En effet, dans une perspective d’enseignement, l’acquisition des notions fondamentales
de base est insuffisante : le maître ne doit pas être seulement quelqu’un qui sait
calculer, bien résoudre des problèmes, qui sait reconnaître dans une situation telle
ou telle structure, il doit être capable d’une réflexion sur la mathématique qu’il
connaît, avoir pris conscience des relations que les structures mathématiques entretiennent
entre elles : les différentes rubriques du programme ne doivent pas être
perçues comme juxtaposées. Une telle réflexion permettra en particulier au maître,
quelle que soit la classe dans laquelle il enseigne, d’avoir pleinement conscience de
la place du jalon qu’il est en train de poser, elle pourra s’appliquer, par exemple,
aux propriétés des structures construites sur \(\mathbb{N}\),\(\mathbb{Z}\), \(\mathbb{Q}\) bien qu’elles ne figurent pas
explicitement au programme. - 3. Organisation de l’enseignement
L’Enseignement Supérieur doit assumer la responsabilité de la formation
théorique.
Une coopération étroite doit exister entre le professeur de l’École Normale
chargé de la formation professionnelle et le professeur de l’Enseignement Supérieur
chargé de la formation théorique. En particulier, les professeurs d’École Normale
devraient pouvoir participer aux cours faits à l’Université afin de pouvoir reprendre
avec leurs élèves des applications des notions théoriques présentées et préparer
leur insertion dans l’enseignement élémentaire.
De même, les responsables de l’Enseignement Supérieur devraient pouvoir
assister - ou mieux participer à des classes ou à des équipes de travail de maîtres
déjà en exercice. - 4. Remarques sur le programme
Ce programme a été élaboré, compte tenu du fait de l’origine actuelle des élèves
(Terminale A). Il est conçu comme une formation initiale permettant de tirer le
parti le plus fructueux d’une formation continue ultérieure.
En particulier aucune place n’a été faite à une approche de la pensée informatique
dont nous savons pourtant qu’elle est nécessaire à la formation des maîtres.
Il faut toutefois remarquer que la situation actuelle est transitoire : le nouveau
programme des classes de deuxième cycle fournira dans trois ans des étudiants déjà
bien familiarisés avec une partie non négligeable du programme proposé. Il faudra
tenir compte de cet acquis sans quoi le programme proposé actuellement n’apparaîtrait
pas comme apportant des notions nouvelles et perdrait une partie de son intérêt ;
il sera donc nécessaire de revoir ce programme d’ici là :
1°afin de reprendre les rubriques actuelles et d’en modifier éventuellement le
contenu ;
2° afin d’envisager l’introduction de rubriques nouvelles - telles que des
notions d’informatique. - 5. Programme de mathématique pour la formation initiale des
maîtres de l’enseignement élémentaire
Le programme est rédigé pour 2 heures hebdomadaires d’enseignement assuré
par l’Université et l heure et demie hedbomadaire d’enseignement assuré par l’École
Normale pendant 2 ans de 32 semaines chacun.
Compte tenu des 24 semaines consacrées aux stages d’observation, au stage en
situation et au stage à l’étranger, cela fait donc 3 heures hebdomadaires assurées
par l’Université pendant les 40 semaines de présence effective des étudiants.
Le programme est rédigé de façon succincte de manière à ce que le responsable
ait une grande liberté pour l’organisation de son enseignement. Afin d’obtenir une
véritable formation, il sera nécessaire de ne pas se contenter d’un enseignement
magistral. Le travail consistera à fournir les connaissances et des applications de
celles-ci et à s’assurer que les connaissances sont effectivement acquises.
- 1. Logique et ensembles finis
Ensembles finis. Cardinaux. Parties d’un ensemble fini.
Relation. Relation d’équivalence ; ensemble quotient ; partition d’un ensemble
fini.
Applications et dénombrements associés.
Connecteurs logiques ; opérations logiques et opérations sur les ensembles ;
algèbre de Boole finie.
Notions sur l’utilisation des quantificateurs. - 2. Ordres
Préordre.
Ordre partiel. Treillis.
Exemples d’ordres totaux. - 3. Algèbre
Monoïde ; relation d’équivalence compatible ; monoïde quotient ; monoïde
ordonné.
Groupe ; définition ; groupe opérant sur un ensemble ; groupes ordonnés ; groupes
cycliques ; générateurs d’un groupe.
Exemples d’homomorphisme de groupes.
Anneaux ; anneaux d’opérateurs. Corps.
Analyse des structures de \(\mathbb{N}\),\(\mathbb{Z}\), \(\mathbb{Q}\).
Systèmes de numération, anneau ordonné des nombres à virgule.
\(\mathbb{Z}\). - 4. Algèbre linéairebr/>
Espace vectoriel de dimension finie. Base. Sous-espace.
Application linéaire, matrices, exemples de calcul sur les n X p matrices notamment
pour \(n \leq 3\) et \(p \leq3\).
Somme directe et projections.
Produit scalaire et norme associée.br/>
Notion d’espace affine.br/> - 5. Fonctions numériques
Réflexion sur les propriétés fondamentales de \(\mathbb{R}\) (la construction de \(\mathbb{R}\) ne sera
pas traitée).
Application linéaire.
Continuité et limites de fonctions numeriques.
Exemples de fonctions numériques (notamment fonctions en escalier, fonctions
affines par morceau). - 6. Mesure et Probabilités
Mesure définie sur une famine de parties d’un ensemble ; additivité ; encadrement.
Dans les cas finis, algèbre des événements ; notion de probabilité.
- 1. Logique et ensembles finis
- 6. Moyens à mettre en oeuvre pour la formation initiale des maîtres
- 1° L’Enseignement Supérieur devant assumer la responsabilité de la formation
théorique, il faut donc que soient créés des postes de maîtres-assistants en quantité
suffisante pour que le travail correspondant constitue une partie du service normal
du personnel que l’assurera. Cela correspond à 1/2, service de maître-assistant par
École Normale, soit 85 postes. - 2° Le temps de travail consacré par le professeur d’École Normale à la mise
au point d’une collaboration efficace entre l’École Normale et l’Université (participation
au cours, élaboration d’exercices d’application des notions théoriques) doit
faire partie du Service des professeurs d’École Normale : cela nécessiterait, dans les
conditions actuelles, la création d’une quarantaine de postes de professeurs agrégés.
Ce problème serait d’ailleurs en partie résolu si les classes de baccalauréat étant
supprimées dans les Écoles Normales, tout le personnel enseignant de mathématique
était affecté à la formation professionnelle de tous les futurs maîtres de l’enseignement
du premier degré.
- 1° L’Enseignement Supérieur devant assumer la responsabilité de la formation
ANNEXE 3.
Bibliographie - Documentation
Les Collègues qui mettront en pratique les recommandations de la Commission
Ministérielle pourront souhaiter une information mathématique complémentaire
ou confronter leurs travaux avec ceux d’autres Collègues engagés comme eux dans
la mise en oeuvre de la réforme.
Lire cette annexe 3 en entier
Supplément au « Bulletin de l’A.P.M.E.P. » n°269 - Juillet-Août 1969
Printed in France
Le Directeur de la publication : G. WALUSINSKI
FD • Imp. Alençonnaise, B. P. 57, 61-Alençon • Dépôt légal 1969 : 8.818 • C.P.P.P. 35.996
<redacteur|auteur=13>































