Quelques propos sur les fonctions en Seconde.

Sommaire

Résumé
Introduction
1. État des lieux
2. Une progression
3. Cinq activités
Bibliographie

Groupe « fonctions » de l’Irem de Strasbourg [1]

Résumé

: Un groupe de recherche dont le nom comporte le mot « fonctions » doit
naturellement s’intéresser à la notion de fonction. Celui de l’Irem de Strasbourg s’est
penché sur l’introduction de cette notion importante en classe de seconde et sur son
interaction avec les autres points du programme. Après avoir analysé le niveau des élèves
en début d’année il propose une progression et des activités pour cette classe.

Introduction

La notion de fonction est centrale au lycée. Un élève de fin de seconde doit être habitué
à utiliser les différents aspects de cette notion. En effet les exigences des programmes
de première et terminale imposent un certaine maîtrise conceptuelle, graphique et
calculatoire de la notion de fonction et de ses propriétés.

1. État des lieux

Étant donné qu’une première approche a été faite au collège, il nous a semblé
important de faire le bilan des acquis des élèves en début de seconde. Pour ce faire, un
test a été donné à des élèves de divers lycées du Bas-Rhin (Lycée de Barr, Lycées
Pasteur, Marc Bloch et international de Strasbourg). Sept classes étaient concernées
(223 élèves). La durée du test était de vingt minutes et il s’est déroulé en début
d’année, avant que la notion de fonction n’ait été abordée.
Énoncé

- Q1.1. La société Rentacar loue des véhicules au tarif suivant : 23 € de prise en
  charge et 0,30 € par kilomètre. Soit x le nombre de kilomètres parcourus, exprimer le
  prix à payer P(x) en fonction de x.
- Q1.2. Imaginer une situation concrète permettant d’obtenir l’expression F(x) = 5x.
- Q2.1. f est la fonction affine \( x \mapsto 3x - 5\), représentée par la droite (d). Calculer
  l’image de \(-\frac{1}{3}\) par f .
- Q2.2. Le point M de coordonnées (3 ; 5) est-il sur la droite (d) ?
- Q3. Parmi les fonctions suivantes, indiquer celles qui sont affines :
  \(f_{1} : x \mapsto 5x \)

\(f_ {2} : x\mapsto \frac{2x}{3} + 1\)

\(f_ {3} : x\mapsto \frac{2}{3x} + 4\)

\(f_ {4} : x\mapsto 2 x^{2} + 3\)

\(f_ {5} : x\mapsto 3-5x\)

\(f_ {6} : x\mapsto \sqrt{5}x-2\)

Bilan par question

Pour la question Q1.1, le taux de
réussite dans les classes est compris
entre 62% et 95%, et pour la question
Q1.2 entre 20% et 47%.

	bonne réponse	mauvaise réponse ou pas de réponse
Q.1.1	78	22
Q.1.2	38	64

Dans la deuxième question,7% des élèves interrogés produisent une réponse où aucune
expression de fonction n’apparaît (pas de variable) et 34% ne répondent pas.
L’énoncé
de Q1.2 a sans doute surpris beaucoup d’élèves mais le mauvais score peut aussi
s’expliquer par une non compréhension de la dépendance entre deux grandeurs
variables liées.

	bonne réponse	mauvaise réponse ou pas de réponse
Q.2.1	49	51
Q.2.2	22	78

Pour la question Q2.1, le taux de
réussite dans les classes est compris
entre 26% et 60 %.
13% des élèves débutent le calcul mais ne le terminent pas, 14% font un mauvais
calcul et 21% ne répondent pas. Mises à part les inévitables erreurs de calcul, il en
sort que le mot « image » est mal interprété par la moitié des élèves.
Pour la question Q2.2, 17% des élèves ont une démarche correcte utilisant un calcul
et répondent de manière cohérente à la question ; 5% font une représentation graphique
correcte et répondent à la question.Les 78% de mauvaises réponses se décomposent
en : 6% où la droite est mal tracée, 38% où la réponse est fausse (mauvaise démarche
de calcul ou justification incohérente dans la plupart des cas) et enfin 33% sans
réponse.
On peut constater que le lien entre le calcul et la représentation graphique n’est fait
que dans 17% des cas. Ce score qui peut, a priori, paraître très faible s’explique par
le fait qu’au collège l’accent n’est pas mis sur ce point. Il appartient donc à
l’enseignant de développer cet aspect en classe de seconde.

Q.3	% de bonnes réponses	f1	f2	f3	f4	f5	f6
		41	75	23	25	41	64

Le taux de non réponse varie entre
5% (pour \(f _2\) et \(f_ 5\)) et 11% (pour \(f_ 1\)
et \(f _3)\).
On peut noter que 4% des élèves reconnaissent en \(f _1\) une fonction linéaire, sans
préciser si elle est affine ou non.
En croisant les réponses aux différentes questions on constate que :

Seuls 2% des élèves répondent correctement aux six questions (4% si on se limite
aux cinq dernières fonctions). Ce très faible taux de réussite s’explique sans doute
en partie par la non reconnaissance de la forme « ax + b » dès que a et b ne sont
plus entiers (naturels). C’est particulièrement remarquable pour \(f _6\), où un élève sur trois n’arrive pas à identifier \(a= \sqrt{5}\) et b=-2
65% des élèves disent que les fonctions \(f _2\) et \(f_ 3\) sont toutes les deux affines. La
distinction entre 2x/3 et 2/(3x) n’est pas perçue dans cette situation.
Enfin 34% des élèves affirment que les fonctions affines sont les cinq dernières.
Pour eux, il semblerait que affine soit synonyme de non linéaire.

Quelles conséquences pour l’enseignement en seconde ?

Il ne s’agit évidemment pas de remettre en cause le travail fait par les enseignants en
classe de troisième : ils ont leurs propres objectifs et trop peu d’heures pour les
atteindre. Trois axes peuvent être dégagés en ce qui concerne le travail des élèves en
seconde.
Tout d’abord, il est indispensable de continuer à travailler la reconnaissance de
forme. Cet aspect du travail n’est évidemment pas spécifique aux chapitres portant
sur les fonctions. Si ce point est négligé en classe de seconde, les élèves ne
dériveront \(\frac{x^{2}}{2}\) qu’en utilisant la dérivée d’un rapport, ou encore développeront
(x − 1)(x + 1) et calculeront son discriminant pour trouver les racines.
Ensuite, dans les chapitres traitant des fonctions, il faut particulièrement insister
sur le lien entre l’aspect géométrique (point sur une courbe) et l’aspect analytique
(coordonnées vérifiant une équation de la courbe). Ce lien, qui semble tellement
évident aux enseignants, n’est pas du tout perçu par une majorité d’élèves arrivant
au lycée. Sans cette base, fondatrice de la géométrie analytique et indispensable
pour aborder l’analyse au lycée, les élèves sont rapidement perdus et en viennent
naturellement à considérer les mathématiques comme des recettes de cuisine.
Enfin, dans le chapitre « fonctions affines », un travail sur les diverses manières
de construire une droite à partir de son équation est indispensable. Ce n’est pas
parce que ce point figure au programme de la classe de troisième que les élèves le
maîtrisent de manière suffisante. Sans ce travail, les notions de tangentes et
d’asymptotes ne pourront pas être mises en place dans les classes de première et
de terminale.

2. Une progression

Comme nous l’avons déjà précisé, la notion de fonction est centrale en classe de
seconde. La possibilité de travailler la partie algébrique du programme en liaison avec
les fonctions permet d’étaler l’introduction de cette notion sur plusieurs mois.
L’importance et la richesse des contenus imposent un fractionnement en plusieurs
chapitres, mais une approche « en spirale », c’est-à-dire un retour fréquent sur les
parties déjà traitées, permet une meilleure appropriation des notions par les élèves.
Nous préconisons, pour ce faire, un découpage en quatre chapitres : généralités,
variations, fonctions affines, fonctions de référence. Dans la présentation qui suit,
nous proposons également pour chaque chapitre une liste d’activités, servant à
introduire ou à travailler les savoir-faire techniques. Cette liste n’est pas exhaustive
mais constitue plutôt un socle minimum. Pour les deux premiers chapitres, nous ne
donnons pas de plan ; les notions nouvelles sont introduites dans les activités et
définies si nécessaire à ce moment.

Chapitre 1 : Généralités sur les fonctions

Activités d’approche
Travailler sur les expressions « en fonction de ».
Reconnaître et manipuler les différentes écritures d’une même expression.
Déterminer l’expression d’une fonction issue d’une situation géométrique ou
autre.

Ces différentes activités seront l’occasion d’introduire ou préciser les notions
suivantes : fonction, variable, ensemble de définition, expression algébrique, tableau
de valeurs, image, antécédent, courbe représentative, équation de courbe.

Activités d’appropriation
Calculer des images « à la main » et avec une calculatrice. Différencier valeurs
exactes et approchées.
Résoudre des équations en lien avec le calcul d’antécédents.
Représenter graphiquement une fonction à partir de son expression algébrique.
Travailler le lien entre les différents registres d’une même fonction. Ce point sera
détaillé dans une activité présentée dans le paragraphe 3.2.
Vérifier si un point appartient ou non à une courbe définie à l’aide d’une équation.
Lire graphiquement des images et des antécédents. Résoudre graphiquement des
équations de la forme f (x) = k ou f (x) = g (x).
Utiliser une calculatrice graphique.

Chapitre 2 : Variations et extremums d’une fonction

Activités d’approche
Étudier des problèmes géométriques ou autres pour introduire la problématique du
chapitre.
Placer des informations dans un tableau de variations.
Travailler la signification de phrases comportant un ou deux quantificateurs
universels.

Ces activités sont destinées à introduire progressivement les tableaux de variations et
les définitions d’extremum et de croissance sur un intervalle.

Activités d’appropriation
Résoudre graphiquement des inéquations de la forme \(f (x) \leq k\).
Construire un tableau de signes à l’aide d’une lecture graphique.
Relever des informations dans un tableau de variations.
Travailler la cohérence entre tableau de variations et courbe.
Obtenir des inégalités à partir des variations d’une fonction.
Utiliser la définition pour obtenir le sens de variations d’une fonction affine

Chapitre 3 : Fonctions affines

1. Représentation graphique d’une fonction affine. Coefficient directeur et ordonnée
à l’origine.
2. Variations des fonctions affines.
3. Signe de ax + b.
4. Caractérisation des fonctions affines.

Activités
Reconnaître si une fonction est affine ou non à l’aide de son expression algébrique.
Construire une droite à partir de la donnée du couple (a ; b). Déterminer
graphiquement un coefficient directeur.
Construire une droite à partir de l’image de deux valeurs bien choisies.
Déterminer le coefficient directeur et l’équation réduite d’une droite à partir des
coordonnées de deux de ses points. Déterminer l’expression d’une fonction affine
connaissant les images de deux nombres.
Déterminer l’image d’un nombre par une fonction affine connaissant les images
de deux autres nombres. Reconnaître si une fonction est affine ou non à l’aide de
la propriété caractéristique : l’accroissement des images est proportionnel à celui
de la variable.
Déterminer le signe de ax + b et appliquer ce résultat à la résolution des
« inéquations-produit ».

Chapitre 4 : Fonctions de référence

1. Fonction carré. Variations et courbe. Application aux équations et inéquations de
type \(x^2 = a\) et \(x^2 < a\)
2. Fonction inverse. Variations et courbe. Application aux équations et inéquations
du type 1/x = a et 1/x > a.
3. Cercle trigonométrique et fonctions sinus et cosinus.

Activités

Encadrer des expressions simples où figurent des fonctions de référence
(enchaînement de fonctions).
Utiliser les propriétés de la fonction carré pour justifier des extremums.
Établir un lien entre propriétés algébriques de f (x) et propriétés géométriques des
courbes (symétries, variations, ...). On revient à cette occasion sur des points
étudiés dans les chapitres précédents.

Voici un diagramme récapitulatif où sont précisés les liens avec d’autres parties du
programme de seconde.

3. Cinq activités

- 3.1. Réfléchir à l’expression « en fonction de … »

Pour introduire la notion de fonction et mettre en évidence cette relation particulière
de dépendance entre deux quantités, il est bon de la présenter sous différents aspects :
tableau, graphique, texte, construction géométrique, … Pour un élève, il est difficile
de faire la différence entre la variable et la quantité qui lui est associée. Cette difficulté
est en grande partie liée au fait que l’ordre de ces deux quantités dans l’énoncé de la
phrase en français est différent de celui dans la notation \(x \mapsto f (x)\). Commencer par ce
travail permet de prévenir, pour un certain nombre d’élèves, la confusion entre x
et f (x).
Sur les exemples présentés, pour les cas qui correspondent à des fonctions, les notions
d’image et d’ensemble de définition peuvent être travaillées. Ceci peut être fait
oralement. En effet, comme pour une langue étrangère, il ne suffit pas à un élève de
lire et d’écouter pour s’approprier le vocabulaire mathématique (ici celui lié aux
fonctions), il doit aussi « parler ce langage » pour pouvoir ensuite l’écrire. Il faut
prendre le temps de l’assimilation du vocabulaire avant d’y ajouter des notions plus
techniques et théoriques.

Énoncé.

Dans le langage courant, on utilise souvent des termes qui expriment une relation de
dépendance ou un lien entre deux quantités. Mais cette dépendance ne traduit pas
toujours une relation fonctionnelle, au sens mathématique, entre les deux quantités.

En effet, il faut savoir qu’en sciences, on dit qu’une quantité y s’exprime en fonction
d’une quantité x lorsque, à chaque nombre x possible, on peut associer une seule
valeur de y. On note alors \(x \mapsto y\) et x est appelé la variable.
Par exemple, l’affirmation « la taille de Marguerite s’exprime en fonction de son âge »
est vraie car à chaque âge on associe une seule taille. On a âge \(\mapsto\) taille et les âges
« possibles » sont des nombres positifs. En revanche, lorsqu’on regarde le relevé
suivant :

Âge (en année)	14	14,5	15	15,5	16	16,5	17	17,5	18	18,5
Poids (en kg)	40	42	40	40,5	42	56	63	62	60	60
Taille (en m)	1,50	1,50	1,52	1,55	1,60	1,64	1,69	1,70	1,72	1,72

on se rend compte que l’affirmation « la taille de Marguerite s’exprime en fonction de
son poids » est fausse, car, par exemple, au poids 40 kg correspondent plusieurs
tailles.

Dire pour chacune des sept affirmations suivantes, si elle est vraie ou fausse, et dans
le cas où elle est vraie la symboliser sous la forme « … \(\mapsto\) … » et donner les valeurs
« possibles » de la variable :
1. Le montant de la facture d’eau s’exprime en fonction de la consommation.
2. Le nombre de personnes venant à la piscine municipale non couverte s’exprime
en fonction de la température extérieure.
3. L’aire d’un disque s’exprime en fonction de son diamètre.
4. D’après le tableau suivant, la consommation de carburant de la voiture étudiée
s’exprime en fonction de sa vitesse :

Vitesse (en km/h)	70	130	60	110	50	90
Consommation (en l/100km)	5,9	10,5	5,5	8,1	5,2	6,3

5. D’après le tableau suivant, la température d’une salle de classe s’exprime en
fonction du nombre d’élèves dans la salle :

Nombre d’élèves	15	24	30	21	35	30
Température(en °C)	19	19,3	19,8	19,3	20,7	20,1

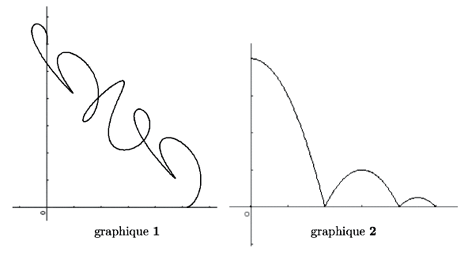
D’après le graphique 1, la hauteur d’un ballon lâché qui se dégonfle étudié ici
s’exprime en fonction de son déplacement horizontal.

7. D’après le graphique 2 la hauteur d’une balle qui rebondit étudiée ici s’exprime en
fonction du temps.

Bilan.

Cette activité a été difficile pour la plupart des élèves et leur a laissé sur le
moment un sentiment de confusion qui leur a fait demander plus d’exercices de ce
type ; ils n’avaient pas l’impression d’avoir compris. Cependant, il ressort qu’il vaut
mieux ne pas s’attarder trop sur ce type d’activité et y revenir ensuite, car elle se
trouve éclairée sous un jour nouveau à la suite du travail sur les fonctions. Cela ne
signifie pas pour autant qu’elle n’a pas sa nécessité car, par le questionnement qu’elle
a instauré, elle participe à la compréhension des activités qui la suivent.

- 3.2. Différents registres pour une fonction

Appréhender le concept de fonction nécessite d’articuler différents registres dans
lesquels une fonction peut être traduite. Il est donc nécessaire de faire travailler aux
élèves ces différents registres (algébrique, graphique, symbolique, tableaux) et de
donner des exercices ayant pour objectif le passage d’un registre à un autre. Dans
chacune des trois situations de cette activité, une fonction est explicitée dans un
registre. Il s’agit de la décrire dans les trois autres. Pour cela l’élève est amené à
construire une stratégie de résolution, le travail ne se faisant pas de façon linéaire.

Bilan.

Les élèves qui sont « à l’aise » en calcul algébrique ont trouvé ces activités
assez faciles. Pour les autres, cela a été l’occasion de revenir sur le sens de la
formalisation dans ce type de calcul : « \(x^2\) représente le carré du nombre x » d’où la
nécessité d’utiliser des parenthèses lorsque x est négatif. Pour ces derniers, le passage
par des exemples est indispensable avant d’aborder le calcul « direct » de l’image d’un
réel par une fonction.
La troisième situation de l’activité a été l’occasion d’une confrontation entre les
différentes stratégies possibles :
Les « laborieux » qui réinvestissent le travail fait avant, en construisant quatre
courbes avant de les comparer à celle donnée. Parmi ceux-là, certains savent déjà
utiliser la fonction graphique de leur calculatrice mais ils ont souvent plus de mal
à choisir entre la deuxième et la troisième expression lorsqu’ils ne s’arrêtent pas
dès la deuxième courbe tracée.
Les « efficaces », peu nombreux, qui arrivent à éliminer rapidement certaines
expressions avant de reprendre une stratégie « laborieuse ».
Pour cette dernière situation un bilan de la stratégie a été dégagé :
On ne peut pas conclure positivement à partir d’une ressemblance (on peut rétroprojeter
la courbe d’équation \(y = 0,5 x^{2}- x + 3, 999\)).
On peut conclure négativement dès qu’il y a dissemblance.

- 3.3. Des carrés dans un carré

Une fois la notion de fonction introduite, on la met en œuvre sur des exemples
simples, et sur lesquels on peut successivement greffer les notions et techniques
nouvelles ou à revoir.
Dans cette activité, nous proposons l’étude d’une situation géométrique qui permet
également de travailler les calculs avec les nombres rationnels ou irrationnels, les valeurs exactes ou approchées d’un nombre, le développement et les identités
remarquables, et pour des valeurs bien choisies, la résolution algébrique d’équations.
En traitant plusieurs activités de ce type, il est possible de ne pas faire de chapitres
séparés pour les notions algébriques rencontrées.
Cette activité peut être reprise dans la partie du programme relevant de l’ordre, pour
étudier l’aire maximale de ce carré, les variations, les résolutions graphiques
d’inéquations.
L’étude faite dans les trois premières questions ne permet pas de répondre à la
question : « Le carré peut-il avoir une aire égale à 20 ? » ; la résolution algébrique de
cette équation étant trop délicate à ce niveau, l’utilisation de la représentation
graphique de la fonction va s’imposer comme méthode de substitution. C’est une
occasion d’utiliser la calculatrice graphique (question 4).

Remarques :

1. Il est possible d’utiliser les TICE pour compléter l’approche faite à la question 1.
2. L’étude de cas particuliers est nécessaire en début d’année pour que l’élève
s’approprie la situation. De plus, c’est une habitude à prendre dans le cas de recherche
de problèmes.

Énoncé.

ABCD est un carré de côté 5. L, M, P et Q sont respectivement les points
des segments [AB], [BC], [CD] et [DA] tels que AL = BM = CP = DQ. On admet
que le quadrilatère LMPQ est un carré (une figure accompagne cet énoncé) et on
se pose les questions suivantes :
Ce carré a-t-il une aire constante ? Peut-il avoir une aire égale à 20 ?
On pose AL = x.

- - 1)
    a) Sur une feuille à petits carreaux, faire la figure pour x = 1, en prenant pour
    unité le centimètre, et estimer à l’aide du quadrillage l’aire de LMPQ. Calculer
    alors l’aire de LMPQ.
    b) Mêmes questions pour x = 2.
  - 2)
    a) Quelles sont les valeurs possibles pour x ?
    b) Exprimer l’aire du carré LMPQ en fonction de x.
  - 3)
    a) On note f la fonction qui à x associe l’aire de LMPQ.
    b) Quelles sont les images de 1 et 2 par f ?
    c) Calculer, lorsque c’est possible, les images par f de 2,5 ; 5 ; 7 ;\(\sqrt3\) ;\(5-\sqrt2\)
  - 4)
    a) Afficher sur l’écran de la calculatrice la représentation graphique de la
    fonction f .
    b) Peut-on construire un carré dont l’aire vaut 20 ?

Bilan.

C’est une activité qui permet aux élèves d’être immédiatement actifs. Le fait
que l’aire du carré LMPQ puisse s’obtenir de deux façons différentes les étonne. En
général ils ne font cette constatation qu’après avoir traité la question 2.b, en comparant avec les autres. Pour les convaincre que 7 n’a pas d’image, il faut souvent
leur demander de faire la figure dans ce cas-là. Lorsque cet exercice est l’occasion de
leur première utilisation de la calculatrice graphique, ils trouvent cet outil plutôt
sympathique et performant. Le réglage de la fenêtre d’affichage est cependant perçu
comme quelque chose de pénible, mais il leur permet de mieux prendre conscience de
ce qu’est l’ensemble de définition de la fonction. Si on leur indique l’utilisation de la
touche « trace » pour contrôler (du moins de façon approchée) leurs calculs de la
question 3.c, c’est ensuite seuls qu’ils finissent l’exercice.

- 3.4. Équations de courbe

La notion d’équation de courbe est, comme il a été dit dans l’introduction, essentielle
à la compréhension de la géométrie analytique. Pourtant il n’est pas rare de trouver
dans des copies de Terminale que l’équation de la tangente T est
T(x) = f ’(a) (x - a) + f (a)
ou même simplement
f ’(a) (x − a) + f (a).
Ceci prouve que, même à ce niveau, la notion d’équation de courbe n’est pas
assimilée.
Un travail spécifique en seconde devrait permettre d’en améliorer la compréhension.
C’est l’objectif des quatre énoncés de cette activité. Comprendre ce qu’est une
propriété caractéristique est au cœur de ce travail ; par ailleurs il permet de faire
remarquer aux élèves la différence, mais aussi le lien qu’il y a entre les deux phrases :
« Tracer la courbe d’équation 3x- 2y + 5 = 0 » et « Résoudre l’équation à deux
inconnues 3x - 2y + 5 = 0 ». Ce travail nécessite sans doute de parler d’équations
équivalentes.
Travailler en binôme pour le premier énoncé permet :
d’obtenir plus de points d’un même ensemble sans que le travail devienne trop
fastidieux ;
à chaque élève de se confronter à plus d’équations ;
des échanges fructueux lorsque les élèves confrontent leurs points de vue.

Énoncé 1 (à faire à deux élèves). — On considère les six relations suivantes :

\(x^{2} +y^{2} = 25 \)

\(3x + 2y - 5 = 0\)

\( xy = 1\)

\(y = x^{2}\)

\( x = y^{2}\)

\(3x-5 = 0\)
Chacun des deux élèves choisit une relation (pas la même !) et fait le travail
suivant :
Soit (O, I, J) un repère orthonormal d’unité 1cm. On considère les points

\( A( 2 ; -0,5) ; B( -\frac{5}{2} ; \frac{25}{4} ) ; C ( \sqrt {13} ; 2\sqrt3) ; D ( \frac{5}{3} ; \frac{3}{5}) ; E(1,21 ; - 1,1 ) ; F(\frac{5}{3} ; - 8) \)

1) Parmi ces points, quels sont ceux dont les coordonnées vérifient la relation
considérée ? Les placer dans le repère.
2) Placer également dans ce repère dix autres points dont les coordonnées vérifient
la relation considérée.
Les deux élèves échangent leur travail puis chacun trouve et place dix points
différents des précédents dont les coordonnées vérifient la relation considérée.
Les deux élèves ensemble étudient les deux travaux et doivent émettre une
conjecture quant à l’ensemble de tous les points dont les coordonnées vérifient la
relation considérée.

Énoncé 2 (d’après un exercice du livre de seconde AXIALE-Hatier édition 2004, page
105).

Phrases :
a. Chaque point a pour abscisse 1.
b. La somme des coordonnées de chaque point est nulle.
c. L’ordonnée de chaque point est égale à l’inverse de son abscisse.
d. Le produit des coordonnées de chaque point vaut −1.
e. L’abscisse de chaque point est égale à son ordonnée.
f. L’ordonnée de chaque point vaut −1.
g. Le carré de l’abscisse de chaque point est égal à son ordonnée.
h. La somme entre le carré de l’abscisse et l’ordonnée de chaque point est nulle.

1) Chacune des phrases de a. à h. caractérise une des courbes de 1. à 8. Relier
chaque phrase à sa courbe.
2) Donner deux équations de chacune des courbes.
3) Si la courbe tracée représente une fonction f , donner l’expression de f en fonction
de x.

Énoncé 3 (d’après un exercice du livre de seconde AXIALE-Hatier édition 2004, page
104).

Pour chaque groupement de points donnés par leurs coordonnées, placer ces points
dans un repère orthonormal d’unité 2 cm (un repère pour chaque groupe) et chercher
celui qui semble s’écarter des autres. Trouver un critère pour décider si un point est
un « intrus » ou non.

Groupe 1. \( A(1 ; 1) ; B(4 ; 2) ; C(2 ; \frac{1}{2}) ; D(\frac{3}{4} ; \frac{4}{3}) ; E (\frac{1}{2} ; 2 ) ; F (\frac{1}{3} ; 3 ) ; G ( 3 ; \frac{1}{3}) ; H ( 5 ; \frac{1}{5}) ; I ( \frac{1}{8} ; 8 ) ; J ( \frac{1}{5}, 5)\)

Groupe 2 . \( A(-2,5 ; -4) ; B(2 ; 5) ; C(1,5 ; 4) ; D (0 ; 1) ; E (2 ; 1) ; F (-1 ; -1) ; G ( \frac{1}{2}) ; 2) ; H (-3 ;-5) ; I ( -\frac{1}{2} ; 0 ) ; \)

Groupe 3. \( A(3 ; 4) ; B(4 ; 3) ; C(5 ; 0) ; D(-4 ; -3) ; E (3 ; - 4) ; F (0 ; 5 ) G ( - 3 ; -4) ; H (- 3 ;4) ; I ( 4 ; -3 ) ; J (8 ; 3) ; K ( - 4 ; 3 )\)

Énoncé 4. Parmi les courbes suivantes, définies par une de leurs équations,
reconnaître :
a) celles qui sont des droites. Donner alors leur équation réduite et les tracer.
b) celles qui représentent une fonction. Définir alors cette fonction.

\(C_1 : 3x + 2y + 10 = 0 \)

\(C_2 : 3 x^{2} + 2y + 10 = 0\)

\( C_3 : 3x + 2y^{2} + 10 = 0\)

\( C_4 : 3x + 10 = 0\)

\( C_5 : 2y + 10 = 0\)

\( C_6 : 3xy = 10\)

\( C_7 : 2x = 3y - 4 \)

\( C_8 : 8y- x^{3} = 0\)

Bilan. Les élèves ont constaté que le choix des valeurs ne pouvait se limiter ni à des
entiers, ni à des nombres positifs. Le travail se fait réellement sur l’équation ; il ne
se limite pas à un simple calcul de f (x) une fois x choisi. La stratégie à utiliser dépend
de la situation. Ils se sont également rendus compte qu’on pouvait trouver si une
courbe représente ou non une fonction sur son équation et donc sans la « voir ».

3.5. À la découverte des variations

Pour illustrer notre point de vue sur les variations de fonctions nous avons choisi une
activité dans laquelle les élèves doivent tracer la courbe représentant les variations
d’une distance en fonction de l’abscisse curviligne d’un point mobile.
Le premier des objectifs est que les élèves constatent que, dans chaque cas, il suffit de
déterminer les couples de nombres (x ; f (x)) pour certains points particuliers, le reste
du tracé de la courbe se trouvant « intuitivement ». Une fois cet objectif atteint, il
semble naturel d’introduire un tableau de variations pour décrire la situation.
Dans un deuxième temps, on peut demander aux élèves de décrire certaines des
situations par des phrases du type : « quand x augmente entre 0 et 5, f (x) diminue »
Ceci constitue un premier pas vers la définition formelle de la croissance (et
décroissance) d’une fonction sur un intervalle. En fin de chapitre, les définitions
(données à l’aide d’inégalités) seront appliquées à des exemples simples (fonctions
affines).

Il nous semble indispensable de débuter cette activité en classe, pour s’assurer de la
bonne compréhension de l’énoncé. L’indication d’une unité de longueur peut aider
certains élèves, ainsi que la visualisation à l’aide d’un logiciel de géométrie
dynamique. On peut demander aux élèves les plus rapides de préciser sur quels
intervalles chacune des fonctions est affine et de donner l’expression de f (x) sur ces
intervalles.

Énoncé. Sur chaque figure, on a représenté un chemin allant de A à B, le point M
se déplaçant sur ce chemin de A vers B. On définit x comme la longueur de la partie
de chemin de A à M et f (x) comme la distance CM. Dans chaque cas, construire la
représentation graphique de f . On ne demande pas forcément un tracé précis.

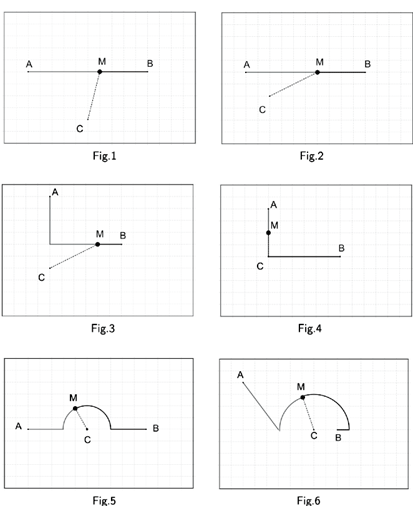
Bilan. Avec plus ou moins de difficultés, d’autonomie et de temps, tous les élèves
arrivent à obtenir des allures de courbes assez honnêtes. L’activité a plu et laisse une
image facilement réactivable. Elle constitue un bon support pour l’introduction des
définitions formelles des variations et des extremums.

Par la suite, dans l’étude d’un problème où la fonction est introduite à partir d’un
support géométrique, certains élèves donnent d’eux-mêmes des indications sur les
variations de la quantité à exprimer avant de chercher son expression analytique.

Bibliographie

[1] L.-M. BONNEVAL (2006), Pour des fonctions qui fonctionnent, Bulletin de
l’APMEP 462, 88–104.
[2] S. COPPÉ, J.-L. DORIER, Y. ILYAS (2007), De l’usage des tableaux de valeurs et
des tableaux de variations dans l’enseignement de la notion de fonction en France
en seconde, Recherches en didactique des mathématiques 27, 2, 151–186.
[3] GROUPE DE LIAISON COLLÈGE-LYCÉE, BASSIN SUD DES DEUX SÈVRES (2005), La
notion de fonction de la classe de sixième à la classe de seconde, Bulletin de
l’APMEP 458, 317–330.
[4] A. MAKHLOUF (Éd.) (2004), Regards et perspectives sur l’enseignement de
l’analyse. Actes du colloque de Mulhouse 8-9 mars 2002, IREM de Strasbourg.