1. Un article de Etienne Ghys et Jos Leys sur le site Image des Maths  [1]

Dans la rubrique « l’objet du mois » de février 2013, Étienne Ghys et Jos Leys
présentent sur le site « Images des Maths » un joli dessin qui ne peut qu’inspirer un
professeur de mathématiques . Voici le début de cet article :

Vous vous souvenez du théorème de Pythagore ?

Le carré de l’hypoténuse
Est égal, si je ne m’abuse
À la somme des carrés
Construits sur les autres côtés .

Partons d’un triangle rectangle très spécial puisqu’il est aussi isocèle. Le théorème
de Pythagore dit précisément que l’aire du grand carré est égale à la somme des
aires des deux petits carrés.

On a bien sûr envie de faire avec chacun des petits carrés ce qu’on a fait avec le grand, comme ceci :

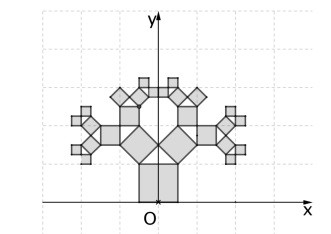
Et on recommence. On obtient un arbre :

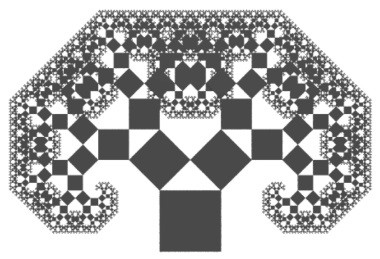
2. L’arbre pythagoricien, un outil pour introduire les suites en classe de Première

Cet arbre nous plonge visiblement dans le monde des suites géométriques. Il est
abordé en classe de Première, et sert d’entrée en matière dans un monde beaucoup
plus vaste : celui des suites. Il accompagne les premières grandes découvertes des
élèves : découverte de « l’infini », de la notion de limite, de l’usage du raisonnement
par récurrence. C’est dans ce contexte que les élèves découvrent par exemple qu’une
somme infinie de termes peut être finie et les antiques paradoxes de Zénon sont
aujourd’hui encore une source sûre d’étonnement extrêmement féconde.
Cet arbre montre un dessin et ce dessin questionne immédiatement. Il offre une
situation riche et motivante.

Citons en d’autres :

La courbe de Von Koch et le triangle de Sierpinski sont devenus des classiques :

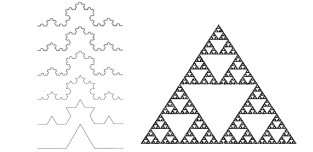
Le document d’accompagnement des programmes de 2001 en proposait plusieurs :

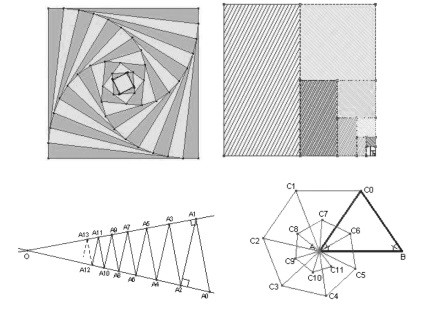
Toute activité de ce type commence par un moment où les élèves s’approprient
l’objet : on dessine à la main quelques étapes pour comprendre le mode de
construction.
Que faire ensuite ? Il s’agit de poser la bonne question : le professeur a toujours
derrière la tête au moins un objectif et l’activité des élèves pour le remplir va
dépendre pour l’essentiel de la question posée.
Bien sûr, on peut n’en poser aucune, et on aura un problème ouvert, qui peut conduire
à tout … ou à rien. Ce type d’activité est certes tentant, mais il demande beaucoup
de temps, denrée rare ; ce n’est pas forcément la meilleure solution.
On peut aussi découper en multiples étapes la marche vers le but, pour que chacun
avance sans encombre, mais les élèves risquent fort de s’ennuyer.
La solution dépend des contraintes du contexte : de quelle plage de temps dispose-t-
on ? Les élèves sont-ils motivés et suffisamment confiants en eux-mêmes pour
chercher en autonomie ? Sont-ils trop nombreux pour que le professeur assure un
suivi individuel des recherches ? Peut-on compter dans cette classe sur des avancées
intéressantes ? L’expérience montre que ce type de situation motive les élèves et que
les idées, en général, ne manquent pas.

Revenons à l’arbre pythagoricien.

La situation est riche et peut être exploitée dans plusieurs directions : la récursivité
en algorithmique, une application des nombres complexes, …

Nous choisirons ici la mise en place des formules donnant le terme général et la somme des n premiers termes d’une suite géométrique et aussi une occasion d’introduire le vocabulaire des suites : suite croissante (le nombre de carrés de
chaque dessin), suite décroissante (l’aire des carrés ajoutés à chaque étape), suite
majorée (la « hauteur » de l’arbre). L’arbre pythagoricien sera alors une activité de
découverte dont les retombées seront l’institutionnalisation des premiers éléments de
base du cours sur les suites.

Dans une classe active et motivée, on peut se permettre de poser une question un peu
« lointaine ». Ici, elle pourrait être, après dessin de l’étape 2 : si on continue, est-ce
que le dessin va forcément sortir de la feuille ?

Dans une classe moins autonome, la question risque de décourager et le
questionnement doit paraître plus abordable pour avoir une chance de motiver les
élèves. Un dialogue avec la classe peut aider à affiner l’analyse du dessin de cette
étape 2 : il y a là des carrés de tailles différentes. Combien de carrés en tout ?
Combien de sortes de carrés ? Combien de chaque taille ? De quelles tailles, si on
commence à un carré de côté 1 ? (La leçon de Socrate sur la duplication du carré dans
le Ménon n’est pas loin, bien sûr… C’est peut-être une occasion de l’évoquer si les
circonstances s’y prêtent !)

Le questionnement pourrait alors se poursuivre par : répondre à ces questions à la vingtième étape puis à l’étape n.

C’est le moment d’utiliser un tableur : le nombre de carrés de chaque sorte donne la
suite des puissances de 2 et le nombre total de carrés est l’occasion d’aborder la
somme de ces puissances. L’intérêt du tableur est de faire apparaître une formule : il
y aura toujours dans la classe un élève assez observateur pour constater que le
nombre de carrés à l’étape n est égal au nombre de nouveaux carrés à l’étape n + 1, diminué de 1.

Ainsi il semble bien que : \(1 + 2 + 2^2 + 2^3 + … + 2^n = 2^{n+1} - 1.\)
On peut le prouver directement par récurrence. On peut aussi faire calculer et simplifier le produit (\(1 + a + a^2 + a^3 + … + a^n \)) (a - 1) pour obtenir une formule plus générale.

On s’intéressera alors à la taille des carrés. Ce ne sera pas si facile ! Mais les souvenirs de collège aidant, les élèves finiront par calculer les côtés des premiers
carrés, puis celui du vingtième, puis celui du n-ième.

C’est l’occasion de faire apparaître une deuxième suite géométrique et celle-ci est décroissante. Pourquoi décroissante ? Parce que sa raison est comprise entre 0 et 1.
Voici encore une pierre à l’édifice.

On peut alors répondre à la première question de l’article : « montrez qu’à chaque étape de la construction, l’aire de l’arbre augmente d’une même quantité, égale à l’aire du carré initial. » Voici donc une suite arithmétique : la somme des aires des carrés successifs.

La moisson est déjà abondante, et on peut s’arrêter là si le temps est compté.

Pour poursuivre l’étude, on pourra choisir de calculer la « hauteur » de l’arbre. La suite obtenue n’est ni géométrique ni somme des termes d’une suite géométrique,
mais les élèves pourront déjà utiliser leurs premiers acquis ; ils trouveront le double de la somme des termes d’une suite déjà utilisée pour donner les côtés des carrés :
1 + 1 + 1/2 + 1/2 + 1/4 + 1/4… Ils vont ici découvrir ce qui plonge toujours bien des élèves dans la stupeur : une suite croissante peut être bornée.

On peut poursuivre en évaluant la « largeur » de l’arbre : on aura besoin ici de considérations géométriques, et bien que l’homothétie et la similitude aient disparu des programmes, les élèves sauront d’eux-mêmes, sans doute, exploiter l’autosimilitude .

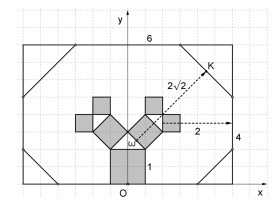
Si on considère le carré le plus à droite de l’étape
no 3, il engendre un arbre « couché » dont la « 
hauteur » est la moitié de celle de l’arbre total. La
« hauteur » de cet arbre est donc 2.
La largeur totale de la feuille minimale est 2 fois
la « hauteur » de l’arbre couché, plus la somme
des diagonales des deux carrés de l’étape 1, soit
une largeur de de 6.

On peut, pour affiner l’étude, passer à un peu de géométrie analytique pour couper au plus près dans le rectangle obtenu les deux coins supérieurs. Prenons le carré de droite de l’étape 2 ; il engendre un arbre oblique qui se déduit de l’arbre total par une rotation de \(\frac{-\pi}{4}\) suivie d’une homothétie de rapport \(\frac{1}{\sqrt 2}\) et d’une translation qu’il n’est pas nécessaire de préciser. La « hauteur » de cet arbre est donc \(2\sqrt 2\). Si on appelle \(\omega\) le milieu de sa base, ses coordonnées dans le repère de la figure sont \(\left( \frac{1}{4},\frac{5}{4} \right)\) ; Le point K de la figure ci-dessus a donc pour coordonnées \(\left( \frac{1}{4}+2,\frac{5}{4}+2 \right)\) ,
soit \(\left( \frac{9}{4},\frac{13}{4} \right)\) . Et on peut découper le coin supérieur droit selon la droite d’équation \(x+y=\frac{11}{2}\)

Finalement on peut enlever en haut deux coins rectangles isocèles de côtés de l’angle droit égaux à \(\frac{3}{2}\) .

En utilisant la demi-largeur du même arbre oblique, qui est \(\frac{3}{\sqrt 2}\), on voit que la figure est au-dessus de la parallèle à (\(\omega\)K), située en-dessous à la distance \(\frac{3}{\sqrt 2}\) , ou, si on compte la distance parallèlement à Oy, à la distance 3, ce qui, puisque (\(\omega K\)) a l’équation \(y = x + 1\), revient à enlever le coin situé sous la droite \(y = x - 2\).

Puisqu’une feuille 4 \(\times\) 6 contient l’arbre tout entier, on en déduit comme l’annoncent les auteurs dans leur article : « à partir d’une certaine étape les carrés de l’arbre finissent par se chevaucher . » Bien sûr, puisque la somme des aires des carrés est
infinie ! Et notre vocabulaire s’élargit : voici une suite bornée (l’aire en vert) et une suite non bornée (la somme des aires des carrés).

On peut évidemment pousser plus loin le jeu et déterminer par exemple la position
des extrémités des cornes spiralées qui sont de part et d’autre du tronc (assez facile)
ou essayer de voir à quelle étape l’arbre commence à se recouvrir lui-même…

Mais quel que soit le temps disponible et le niveau de la classe, l’objectif sera
largement atteint et la récolte suffisamment abondante pour ramasser les morceaux
et mettre en place les premiers éléments de cours prévus !

Merci à Étienne Ghys et Jos Leys pour ce bel objet qui s’avère riche et efficace.

Complément à cet article :
un programme en Amiens-Python dû à Bernard Langer, permettant de construire l’arbre pythagoricien.

<redacteur|auteur=500>