Énoncés des nouveaux problèmes

Problème 509-1
Soit f,g : \(\mathbb R^*_+ \rightarrow \mathbb R\) deux fonctions intégrables sur \(\mathbb R^*_+\). Montrer que la fonction

$$(x,y) \mapsto \frac{f(x)g(x)}{x+y}$$

est intégrable sur \(\mathbb R^*_+ \times \mathbb R^*_+\) et trouver la meilleure constante C>0 telle que

$$ \left | \iint_{]0,+\infty[ \times ]0,+\infty[} \frac{f(x)g(x)}{x+y} dxdy \right |\le C \sqrt{\int_{]0,+\infty[} f(x)^2 dx}\sqrt{\int_{]0,+\infty[} g(y)^2 dy}$$

voir l’article où est publiée une solution

Problème 509–2 (Michel Lafond)
On appelle couple moyen tout couple d’entiers naturels (a, b) avec 0 < a < b tels que leur moyenne arithmétique \(m=\frac{a+b}{2}\) leur moyenne géometrique \(g=\sqrt{ab}\) et leur moyenne harmonique \(h=\frac{2ab}{a+b}\) soient des entiers naturels. Par exemple, (a, b) = (10, 40) est un couple moyen puisque m = 25, g = 20, h = 16.
(1) Trouver tous les couples moyens.
(2) Montrer que si (a, b) est un couple moyen dont les moyennes valent m, g, h, alors (m - g, m + g) est un couple moyen.
(3) Si (a, b) est un couple moyen, la moyenne quadratique \(q=\sqrt(\frac{a^2+b^2}{2}\) peut-elle être entière ?

Problème 509–3 (Michel Lafond)
Si n est un entier supérieur ou égal à 3, on pose \(A=2 \sin\left ( \frac{\pi}{n} \right )\). Dans le plan muni d’un repère orthonormé, on définit la suite de points \((M_k(x_k,y_k))_{k \in \mathbb N}\) par

$$M_0(1,0)$$

et pour k ≥ 1 (attention aux indices),

$$x_k=x_{k-1}-Ay_{k-1} \ \ \ \ \ \ \ \ \ y_k=y_{k-1}-Ax_k.$$

Par exemple, pour n = 8, voici les 9 premiers points de la suite :

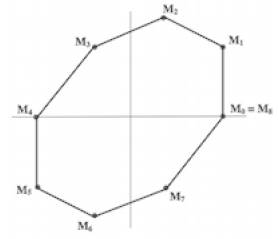
(1) Montrer que cette suite de points est périodique de période n.
(2) Montrer que tous les points de la suite sont situés sur une même ellipse.
(3) Montrer que l’aire du polygone (\(M_0M_1…M_{n-1}\)) est comprise entre \(\pi - \frac{\pi^3}{6n^2}\) et \(\pi\)

Solutions des problèmes antérieurs

Problème 501–2 (Michel Lafond, Dijon)

Soit \(c \in \mathbb{N}\) et K la suite définie par

$$K_0= 0, K_1= 1\ \text{ et pour } n \ge 2 \ \ K_n= (c - 2)K_{n-1}- K_{n-2}+ 2.$$

Montrer que si c est un carré parfait, alors tous les \(K_n\)
sont des carrés parfaits.

Solutions de Michel Bataille (Rouen), Maurice Bauval (Versailles), Jean-Claude Blanchard (Brunoy), Hélène Brion (Clamart), Richard Choulet (Caen), Bernard Collignon (Coursan), Clement Durringer, Michel Lafond (Dijon), Pierre Renfer (Saint Georges d’Orques).

Problème 502–1 (Gauthier Gidel, Alexandre Benchaouine, Benoît Joly)
Soit \(n \in \mathbb N\)* , \(x_1, …, x_n\) des réels strictement positifs et \(p_1, …, p_n\) des réels strictement positifs de somme 1. Pour tous les réels S et t vérifiant, pour tout \(i \in [1]\),

$$S \le \sqrt{x_i} \le S+t$$

montrer que

$$\frac{1}{\sum_\limits{i=1}^{n} \frac{p_i}{x_i} } \le \sum_\limits{i=1}^{n} p_i x_i \le \frac{1}{\sum_\limits{i=1}^{n} \frac{p_i}{x_i} } + t^2$$

Solutions de Michel Lafond (Dijon) et Pierre Renfer (Saint Georges d’Orques).

<redacteur|auteur=500>