Claude Gachet

Trois situations « courantes » pour lesquelles nous avons envisagé des modèles
accessibles aux élèves :
 * La réfraction de la lumière vue comme une course entre deux rayons.
 * Les marées : comment connaître la hauteur d’eau à une heure donnée ?
 * Répartition des barrettes sur le manche d’une guitare : présentée comme recherche
d’une unité commune.
Le but de cet atelier était de présenter des situations, à partir de véritable questions
pouvant servir à rendre opérationnelles des connaissances mathématiques acquises,
voire éventuellement à introduire ces connaissances. Dans chaque exemple le
minimum de renseignements est donné ; en souhaitant que chacun en prenant
connaissance de la situation exprime le besoin de tel ou tel renseignement ; charge
au responsable de fournir ces renseignements s’ils apparaissent nécessaires après
discussion.

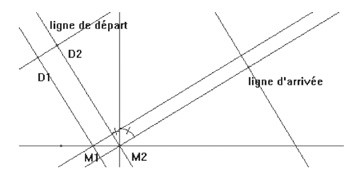
La première situation présentait une course entre deux concurrents suivant deux
trajets parallèles jusqu’à une ligne puis repartaient en suivant à nouveau des trajets
parallèles. La question était de savoir si les trajets étaient équitables.

Il s’avère que les trajets suivis sont de même longueur si et seulement si « l’angle
d’incidence est égal à l’angle de réflexion ».

Le deuxième aspect partait de la même idée mais cette fois les concurrents couraient
dans le sable jusqu’à la ligne qu’ils franchissaient avant de courir dans l’herbe (donc
avec des vitesses différentes).

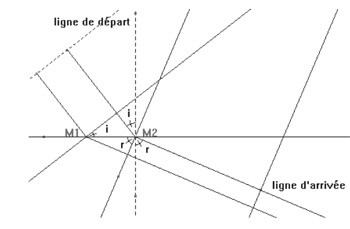
Là encore nous retrouvons l’égalité des trajets, égalité en temps cette fois, si et
seulement si \( \frac{sin (i)}{v_{1}} = \frac{sin (r)}{v_{2}}\)

Ces lois de la réflexion et de la réfraction sont au programme de physique de
seconde.

N’entrent en jeu dans cette étude que des notions de géométrie vues en Troisième.

Pour aller plus loin dans ce domaine vous pouvez visiter le site Académie de
Grenoble Planète Maths.

La deuxième situation demandait s’il était possible de rentrer dans le port de La
Rochelle en cet après-midi du 26 octobre aux environs de 16 heures dans une
embarcation nécessitant 4 mètres de hauteur d’eau.

Les participants ont demandé les données utiles : heures et amplitudes des marées de
ce jour.

L’idée était de tester plusieurs propositions de modèles pouvant venir naturellement ; par exemple un modèle affine par morceaux, un modèle sinusoïdal, un modèle en
créneau, …

Bien sûr le temps ne nous a pas permis de tous les étudier ; par contre, en classe il
serait utile de le faire faire aux élèves. Nous avons pris plus de temps pour mettre en
place le modèle sinusoïdal ; la recherche des paramètres, amplitude, phase, et
pulsation, est intéressante à faire en classe.

Enfin nous avons comparé ce modèle avec ce que donne la « règle des douzièmes »
très utilisée en navigation. Cette règle dit que pendant la première heure la mer monte
de 1/12 de son amplitude totale, pendant la deuxième heure elle monte de 2/12,
pendant la troisième heure elle monte de 3/12, puis à nouveau 3/12, puis 2/12, puis
1/12 (la marée durant environ 6 heures on arrive ainsi à la pleine mer). Durant la
descente on se retrouve avec la même répartition.

Placer ces « points » sur la même représentation graphique que ceux que donnaient
les autres modèles (à l’aide d’une calculatrice graphique) est instructif :

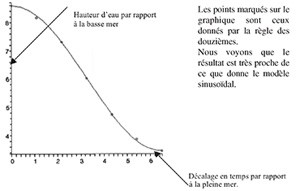
Les points marqués sur le
graphique sont ceux
donnés par la règle des
douzièmes.
Nous voyons que le
résultat est très proche de
ce que donne le modèle
sinusoïdal.

La troisième situation partait de l’observation de ce qui se passe lorsqu’une corde
de guitare entre en vibration.

On a constaté en déplaçant un doigt juste posé sur la corde (sans pression afin que la
corde ne touche pas les barrettes-frettes) qu’il y avait deux positions, l’une située au
tiers de la longueur, l’autre située à la moitié, pour lesquelles la corde conservait un
son qui n’était pas un bruit désagréable. D’où la mise en évidence de deux écarts
naturels dus à la présence d’harmoniques). Le premier est celui que l’on a dans la
chanson « là-haut sur la montagne » entre le « là » et le « haut » ; il est caractérisé
par le rapport 1/2. Le second est celui que nous avons dans « frère jacques » entre le
« frè » et le « vous » de dormez-vous . il est caractérisé par le rapport 2/3 (la longueur
de corde restante est égale à 2/3 de la longueur de corde initiale.

Une autre constatation : un écart entre deux notes (jouées sur une même corde) est quantifié par le rapport des longueurs de la corde qui entre en vibration. Cette notion
d’écart peut être « contrôlée » à l’aide d’une chanson chantée à différentes hauteurs.

Deux écarts « mis bout à bout » en donnent un troisième qui sera caractérisé par le
rapport \( \frac{L_3}{L_1}= \frac{L_3}{L_2}x \frac{L_2}{L_1}\).

Donc ajouter deux écarts se traduit par faire le produit des
rapports associés (on peut aussi se reporter à la loi de Weber-Fechner).

La question posée est alors de trouver un « écart standard », qui puisse servir
d’« écart unité » ; c’est à-dire-un écart qui « mis bout à bout » avec lui-même
plusieurs fois puisse donner les deux écarts découverts plus haut.

Nous pouvons traduire cela par la recherche d’un rapport q et de deux exposants n et
m tels que \(q^n\) soit égal à 2/3 et \(q^m\) soit égal à 1/2.

Ce problème a-t-il une solution ? Une petite étude arithmétique nous dit que non.
Reste à voir si nous pouvons trouver une solution approchée. Le tableau ci-dessous
nous éclaire :

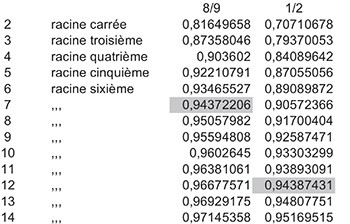
Les deux cases grisées donnent
des valeurs assez proches. Donc
si nous prenons q = 0,9438 nous
aurons à l’enchaîner 7 fois pour
retrouver l’écart correspondant à
2/3, et 12 fois pour retrouver
celui correspondant à 1/2.

Autre approche : on a \(q^{n}= 2/3\) et \(q^m = 1/2\) donc \(q^{2n-m}= \frac{8}{9}\) ; on s’aperçoit vite que
8/9 ne peut pas servir d’écart unitaire, mais que sa racine carrée convient
approximativement.

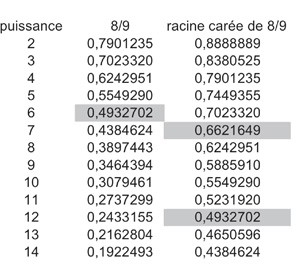
Nous voyons dans la seconde colonne que
0,5 est bien approximativement une
puissance de 8/9 ; mais pas 2/3.
Par contre dans la troisième colonne nous
trouvons approximativement 1/2 et 2/3.
Donc \(\sqrt{\frac{8}{9}} \) convient approximativement
comme écart unité.
Il admet 0,943 comme valeur approchée.

Il faut 7 écarts-unité pour obtenir le premier écart naturel, et 12 écarts-unité pour
obtenir le second écart naturel. C’est effectivement le nombre de barrettes que nous
comptons sur le manche de la guitare ; l’écart unité trouvé est le demi-ton.

Ces considérations peuvent paraître hermétiques mais si on prend le temps de
travailler sur les enchaînements d’écarts on constate vite qu’ils se traduisent par des
produits de rapports. D’autre part les logarithmes peuvent beaucoup simplifier les
choses puisqu’ils transforment ces produit en sommes ; alors la recherche d’une
« unité » devient représentable sur une droite.

Je tiens à remercier chaleureusement tous les participants à cet atelier pour leur
spontanéité et leur indulgence.