par la Commission de Réflexion
sur l’Enseignement des Mathématiques ( CREM)

Les textes présentés ici [1] prolongent les deux rapports d’étape de la CREM :
Informatique et enseignement des mathématiques et Formation des maîtres.
Ils se
situent dans la perspective de travaux pratiques de mathématiques, de nature
algorithmique conduits assez largement (mais non exclusivement) sur ordinateur et
abordables au lycée pour la plupart. Leur conception illustre par quelques exemples
choisis la possibilité de développer des activités en algorithmique sous la direction
d’un professeur de mathématiques.

Table des matières
 1. Qu’est-ce qu’un algorithme ?
 2. Nombres et arithmétique
 3. Jeux de chiffres et mathématiques expérimentales
 4. Algèbre et géométrie
 5. Analyse : intégration numérique
 6. Statistique et probabilités : les aiguilles de Buffon
 7. Graphes : recherche de la distance entre deux sommets
 8. Quelques algorithmes abordables au Lycée

Les principes qui sous-tendent ce document sont les suivants :
 Le point de vue constructif et expérimental confère aux objets mathématiques une
existence concrète dès lors qu’on les manipule ou les anime sur ordinateur. C’est
l’occasion d’une découverte personnelle par l’élève de « phénomènes »
mathématiques, propre à susciter l’intérêt de bon nombre d’entre eux. Ce point de
vue offre un éclairage transverse à différentes parties du cours de mathématiques et
en renforce tout naturellement le message.
Ainsi, voir l’algorithme d’Euclide « tourner » éclaire la notion abstraite de
coefficients de Bézout ; trouver soi-même les bonnes approximations \( \frac{22} {7}\) et \( \frac{355} {113}\) de
\(\pi\) par l’algorithme des fractions continues est une expérience valorisante
– l’humanité a mis plusieurs siècles à les dégager –. Expérimenter avec \( \sqrt{2}\) ou le
nombre d’or permet à l’élève de découvrir des phénomènes facilement explicables
dans le cadre du programme de terminale (le point fixe d’une homographie).
Voir
l’algorithme de Newton et une méthode d’itération converger (ou diverger) place, par
le calcul, l’élève en prise directe sur des problèmes de nature mathématique déjà abordés dans le cours (quand et pourquoi y a-t-il convergence ?). Simuler forme à
l’interprétation de données statistiques de toute nature, illustre concrètement des
points de statistique et probabilités récemment introduits dans les programmes, et
peut même servir de point de contact avec d’autres disciplines (simulation de la
désintégration radioactive par exemple).
 Le type d’activité proposé correspond à une initiation douce à l’insertion de
l’informatique dans l’activité scientifique. Il convient d’éviter que l’ordinateur soit
perçu comme une boite noire « fournissant des réponses forcément justes » et
« raisonnant à notre place » pour peu que l’on sache presser les bons boutons. Les
activités d’algorithmique proposées indiquent tout au contraire à l’élève la possibilité
d’une utilisation critique et réfléchie de l’informatique.
Les activités d’algorithmique doivent ainsi être conduites dans la perspective de
l’acquisition par l’élève de quelques concepts et principes fondamentaux. Un
ordinateur se programme, un programme est la traduction en langage formalisé d’un
algorithme, un algorithme est un procédé de calcul enraciné dans les mathématiques.
<br<Nous revenons ci-dessous sur ces points.
 Il importe d’éviter soigneusement l’ajout d’un chapitre supplémentaire
d’algorithmique aux programmes. Les thèmes type développés ci-après sont conçus
pour être « dans le programme » (les quelques incursions en limite de programme ou
hors programme ne sont mentionnées qu’en tant qu’options abordées sous l’angle
expérimental ou comme activités d’éveil mathématique). Cette partie de
l’enseignement de mathématiques n’a ainsi aucunement prétention à couvrir
l’ensemble de la discipline informatique. Ce qui est proposé ici constitue une voie
implantable assez rapidement avec les moyens humains disponibles et des volumes
horaires nécessitant une adaptation des programmes plutôt qu’une véritable
révolution.
Il convient cependant de ne pas sous-estimer la nécessité d’adapter la formation des
professeurs à ces objectifs. Cela suppose un effort certain de formation continue ainsi
qu’une inflexion de la formation initiale des professeurs qui doit s’enrichir [2] d’une
initiation aux concepts de l’algorithmique et aux bases logiques de la
programmation.

1. Qu’est-ce qu’un algorithme ?

Un algorithme, tel que défini par l’Encyclopedia Universalis, consiste en la
spécification d’un schéma de calcul sous forme d’une suite d’opérations
élémentaires obéissant à un enchaînement déterminé. On sait que le nom vient de
celui de Al Khwarizmi [780-850], dont le livre inspiré de la tradition indienne décrit
(entre autres choses) les méthodes de calcul effectif pour les opérations sur les entiers
exprimés en base 10.
De grands mathématiciens classiques, de Newton à Euler et Gauss, ont déjà une pensée largement algorithmique, bien avant même que
l’informatique ne soit inventée.
Le point de départ, l’algorithme, est ainsi une méthode de calcul qui, considérée avec
assez de précision, pour des données sous une forme bien spécifiée à l’avance, pour
des opérations qui sont effectives, conduit en un nombre fini d’étapes à un résultat lui
aussi sous une forme bien spécifiée à l’avance. La description d’un algorithme
s’exprime donc dans le langage mathématique usuel, tout en bénéficiant de sa
souplesse. Le passage d’une notion intuitive de « procédé de calcul » à une
description algorithmique nécessite un premier effort de réflexion logique et de
formalisation qui possède une valeur éducative certaine car indépendante des
technologies du moment.

La précision logique de l’expression prépare enfin efficacement à l’écriture d’un
programme, lequel est vu comme la transcription de l’algorithme dans un langage
particulier directement interprétable par l’ordinateur.

Plus précisément, les algorithmes décrits ci-dessous reposent sur une base
minimale [3] qui est la suivante :
 la notion de variable et d’affectation (a := b ; a ← b ; b → a) ;
 les conditions, si… alors… sinon ;
 les connecteurs logiques de base, et, ou, non ;
 les itérations ou « boucles » pour, tant que ;
 quelques notions simples sur les tableaux, matrices (ces dernières vues comme
tableaux de nombres) ;
 la procédure ou fonction en tant que mode de structuration des programmes.

Dans cet esprit, les textes qui suivent décrivent essentiellement des algorithmes. Le
niveau de précision des commentaires et des descriptions montre assez que la
traduction dans un langage de programmation donné (de la calculatrice au microordinateur)
est immédiate, dès qu’ont été acquises quelques règles syntaxiques de
base du système sous lequel on doit pratiquer. Nous avons choisi de présenter des
algorithmes classiques, tous accessibles quant à leur contenu mathématique, à un
élève de lycée.

On verra sur ces exemples qu’il ne s’agit pas de se limiter aux seules primitives de
base d’un langage de programmation existant. On se permettra aussi de travailler
dans un environnement contenant un certain nombre de fonctions ou procédures
clairement répertoriées. Le partage de programmes sur Internet ainsi que l’existence
de très nombreux logiciels et systèmes aux fonctionnalités étendues (MATLAB et la
version publique SCILAB, les systèmes de calcul formels comme MAPLE, DERIVE, PARI ou MATHEMATICA, les nombreuses bibliothèques multiprécision)
autorisent cette démarche.

Bibliographie.

On trouvera dans le chapitre 1 du célèbre livre de Donald Knuth, The
Art of Computer Programming [4], une discussion sur l’origine du terme et sur les
différents sens qui lui ont été prêtés au cours du temps. On peut voir cette annexe
comme une incitation à lecture de ce livre et de ceux que nous avons pillés [5].

Sur
l’aspect expérimental en mathématiques, on pourra consulter les pages du site
Internet du Center for Experimental and Constructive Mathematics de Vancouver au
Canada.

Sur l’histoire des mathématiques, une référence Internet est le site The
MacTutor History of Mathematics archive de l’université de St Andrews en Écosse.

Le point de vue historique en algorithmique est traité de manière inspirante par
l’ouvrage Histoires d’algorithmes [6]

2. Nombres et arithmétique

Les algorithmes les plus connus et pratiqués sont sans doute ceux qui traitent des
quatre opérations sur les nombres entiers. Dans la tradition et l’enseignement ils sont
étroitement liés au système de numération décimale. L’ouvrage de Al Khwarizmi
décrivait à la fois le système de représentation décimale des entiers et la façon
d’effectuer les opérations.

Évaluer les performances ou l’efficacité d’un algorithme (sa complexité) n’a de sens
que si l’on a bien précisé la structure des données (format des entrées et sorties). Par
exemple, un algorithme d’addition de deux entiers ne sera pas le même suivant que
les entiers sont représentés en base 10 ou en base 2 (on pourrait même distinguer
suivant la façon effective dont la suite des chiffres est représentée : liste, tableau, …).
On conçoit également que de nombreux algorithmes ont pour but la conversion d’une
représentation à une autre d’un objet : par exemple, passer de la représentation d’un
entier en base 10 à celle en base 2 et inversement.

Ces conversions, souvent non triviales, sont quelquefois masquées par la vision
polymorphe que nous avons des objets mathématiques. Les mettre en évidence peut
clarifier certains aspects de ces objets.

Par exemple, supposons donné l’algorithme d’addition de deux entiers exprimés en
base 10. Un nombre décimal est représenté comme un « nombre à virgule » appelé
par les informaticiens « flottant ». Comment obtenir un algorithme d’addition des
décimaux ?

On commence par écrire l’algorithme de conversion qui, à partir de la
représentation « nombre à virgule », fournit la représentation du décimal comme produit d’un entier par une certaine puissance de 10 (et inversement). Ajouter 1,37 et
0,978 1 se ramène alors à ajouter \(9 781x10^{-4}\) et \(137x10^{-2 }\) également représenté par
\(13 700x10^{-4}\), ce qui donne, en utilisant l’addition des entiers, \(23 481x10^{-4}\) et
finalement, après une dernière conversion 2,348 1.

On constate que le pas essentiel pour passer de l’addition des entiers à celle des
décimaux est un algorithme de conversion entre deux représentations des dits
nombres décimaux.

On peut être aussi tenté de représenter un entier par sa décomposition en produit de
facteurs premiers. Cette structure de données est très avantageuse lorsqu’il s’agit de
calculer le pgcd de deux entiers ou plus généralement d’étudier les questions de
divisibilité. Cependant, on paiera le prix fort au moment d’effectuer l’addition de
deux entiers : il faudra factoriser le résultat pour qu’il soit sous la forme requise. Il
s’avère que c’est en général coûteux.

Finalement, compte tenu de ces considérations sur le coût de la factorisation,
l’algorithme d’Euclide est efficace pour calculer le pgcd de deux entiers à partir – par
exemple – de leur représentation décimale. On peut en donner des variantes adaptées
au format des entrées et sorties.

 2.1. Algorithme d’Euclide

L’existence du plus grand commun diviseur de deux entiers, le théorème de Bézout
sont des résultats importants qui sont étudiés au cours du programme de terminale S
(spécialité mathématiques). L’algorithme d’Euclide est non seulement l’outil pour
effectuer des calculs effectifs mais son étude a priori permet de mettre en évidence
des propriétés arithmétiques et de démontrer ces énoncés.

 2.1.1. Division euclidienne des entiers

On part de la procédure suivante, écrite dans un langage presque réel.
(l’expression x ← y signifie que la valeur de la variable x est remplacée par la valeur
de la variable y au moment de l’opération ; le résultat de la procédure est la dernière
expression calculée).
Procédure Division euclidienne
Entrées : a ≥ 0, b > 0, entiers.
Sorties : r, q, entiers.
Initialisation : j := 0, \(\alpha := a.\)
Tant que α ≥ b faire (α, j) ← (α − b, j + 1).
retourner (r, q) ← (α, j).
Il s’agit bien sûr de l’algorithme « naïf » de division par soustractions successives.
Cet algorithme démontre que la division est réductible à la soustraction. Raisonner
sur son fonctionnement met en évidence sur un exemple simplissime l’interaction
entre propriétés des objets mathématiques abstraits, la correction et la terminaison
d’un algorithme, et l’efficacité (ou complexité) du calcul. Que peut-on en tirer ?
 1. Cette procédure produit-elle un résultat ? Autrement dit est-ce que l’algorithme
décrit ici s’arrête dans tous les cas au bout d’un nombre fini de pas ? On voit que oui et que le nombre de pas est majoré par a. En sortie, on obtient deux
entiers r et q qui vérifient a = bq + r avec 0 ≤ r < b.
 2. Tous les résultats intermédiaires et donc le résultat final (reste et quotient) sont
des entiers. Les seules opérations mises en jeu sont la comparaison de deux
entiers et la soustraction \(\alpha-b\) lorsque \(b\leq\alpha\). La division euclidienne est donc
une opération sur les entiers et uniquement sur les entiers.
 3. La procédure décrite ici semble indépendante de la façon dont on a représenté
les entiers, en particulier de la base de numération. Ce n’est qu’en partie vrai.
Il faut disposer, outre d’une façon de représenter les entiers, d’algorithmes
permettant de comparer et de soustraire des entiers qui, eux, peuvent dépendre
de la représentation des entiers choisie.
 4. Lien avec la divisibilité : dans le pas élémentaire de l’algorithme
\((\alpha, j) \leftarrow(\alpha-b, j + 1)\)
l’ensemble des diviseurs communs à \(\alpha \) et b est un invariant. L’ensemble des
diviseurs communs à \(\alpha \) et b est donc l’ensemble des diviseurs communs à r et b.
 5. On peut également remarquer que la sortie (r, q) est l’unique solution au
problème de la décomposition a = bq + r avec 0 ≤ r < b, tandis que q est
l’unique solution au problème bq ≤ a < b(q + 1). En particulier on peut noter
que ce dernier problème est équivalent à celui de la division euclidienne de a
par b.
 6. En revanche, on constate que l’algorithme qui produit le seul reste de la
division de a par b est simplement :
Procédure Reste modulo b.
Entrées : a ≥ 0, b > 0, entiers.
Sortie : r, entier.
Initialisation : \(\alpha := a\)
Tant que \(\alpha \geq b\) faire \(\alpha \leftarrow \alpha-b\).
retourner \(r \leftarrow \alpha\)
 7. Comment accélérer l’algorithme de division euclidienne ? On peut essayer de
télescoper plusieurs étapes élémentaires. On peut voir comment on le met en
œuvre dans l’algorithme de division en base 10 pratiqué à l’école. On constate
sur cet exemple précis qu’il y a une différence notable entre savoir exécuter un
algorithme sur tout exemple et écrire la procédure correspondante. Surtout, on
s’aperçoit à cette occasion que l’algorithme soustractif de départ a une
complexité exponentielle (!) en le nombre de chiffres des opérandes, alors que
l’algorithme dérivé dépend de manière simplement polynomiale de ce même
nombre de chiffres.
 8. Évaluer les différentes complexités : les majorer, les minorer. Pour cela il faut
définir les opérations élémentaires et leur coût. Elles sont ici la comparaison de
deux entiers et la soustraction. On estimera la complexité de l’algorithme de
division en fonction de la taille des entrées (valeur absolue, nombre de chiffres
de l’écriture, …).
Signalons que cet exercice n’est pas qu’un exercice d’école. Les ordinateurs
fournissent des primitives de calcul opérant sur des entiers bornés par \(2^{32}\) ou \(10^{15}\) (par
exemple). Si l’on veut dépasser ces limites, il est nécessaire de programmer.
Les
programmes correspondant peuvent être écrits par l’élève ou utilisés plus ou moins
silencieusement à partir de ce qui est disponible sur Internet et dans les logiciels
existants. Voir par exemple le calculateur Pari/Gp issu de l’université de Bordeaux
qui est un logiciel libre.
FIG. 1 – Une calculatrice multiprécision (ici Gp) cache de fait
une bibliothèque d’algorithmes et de programmes sur les entiers.

De tels logiciels ne servent d’ailleurs pas qu’aux mathématiciens : comme l’on sait,
des millions de transactions électroniques sont chaque jour protégées par le système
cryptographique RSA [7]) qui repose sur la manipulation arithmétique d’entiers
comportant plusieurs centaines de chiffres binaires.

EXERCICE : Écrire les procédures d’addition, soustraction, multiplication et division
en base 10 pour des entiers pouvant aller jusqu’à 1000 chiffres décimaux (par
exemple). Un « grand entier » pourra être représenté par un tableau de nombres entre
0 et 10. Réaliser à partir de là une implantation de « grands flottants ».

2.1.2. Algorithme d’Euclide : calcul du pgcd

Donnons une forme de l’algorithme d’Euclide :
Procédure Algorithme d’Euclide
Entrées : a ≥ 0, b ≥ 0, entiers.
Sortie : pgcd(a, b), entier.
Initialisation : α := a, β := b
Tant que α ≥ 0 et β ≥ 0 faire
si β = 0 retourner α et sortir
si 0< β ≤ α faire (α, β) ← (α − β, β)
si 0≤ α < β échanger (α, β) ↔ (β, α)

 1. Pour chaque entrée l’algorithme s’arrête au bout d’un nombre fini de pas. En
écrire une version utilisant la procédure « Division euclidienne ». Là encore la
procédure porte sur les entiers et seulement sur les entiers. Il suffit de savoir les
comparer et les soustraire (cf. 2.1.1.2).
 2. On remarque que l’ensemble des diviseurs communs à α et β est conservé par
les étapes élémentaires tout au long de la procédure, ce qui prouve l’existence
du plus grand commun diviseur, c’est-à-dire d’un entier dont les diviseurs sont
les diviseurs communs à a et b.
Remarquer aussi que le résultat de la procédure est une combinaison de a et b
à coefficients entiers (Bézout). (voir 3 ci-dessous).
 3. Comment produire cette combinaison linéaire ?
On remarque qu’il suffit d’écrire chaque résultat intermédiaire comme une
combinaison linéaire de a et b, en commençant par les relations triviales
a = 1.a + 0.b, b = 0.a + 1.b.
On écrit donc une forme de l’algorithme d’Euclide étendu en tenant compte de
ces simples observations
Procédure Algorithme d’Euclide étendu
Entrées : a ≥ 0, b ≥ 0, entiers.
Sortie : pgcd(a, b), u, v, entiers.
Initialisation :
α := a, β := b ;
λ := 1, μ := 0 ;
ρ := 0, σ := 1
Tant que α ≥ 0 et β ≥ 0 faire
si β = 0 retourner (α, λ, μ) et sortir
si 0 < β ≤ α faire (α, β, λ, μ, ρ, σ) ← (α − β, β, λ − ρ, μ − σ, ρ, σ)
si 0 ≤ α < β échanger (α, β, λ, μ, ρ, σ) ↔ (β, α, μ, λ, σ, ρ)

 4. Suivant les sorties souhaitées, on peut raffiner ou simplifier les algorithmes
présentés. Par exemple, partant d’un couple d’entiers (a, b) premiers entre eux,
on cherche à calculer le seul coefficient u d’une relation de Bézout au + bv = 1,
i.e. l’inverse de a modulo b. On voit d’ailleurs qu’à partir de ce dernier calcul,
il est facile de récupérer v.
 5. Importance de la structure des données. Supposons que a et b soient deux
entiers écrits en base 2. On peut calculer leur pgcd à l’aide de la procédure
définie ci-dessus. Cependant on peut utiliser la remarque suivante : la puissance
de 2 qui divise un entier est le nombre de zéros consécutifs à droite de son
écriture en binaire.
Donnons un exemple : calculons le pgcd des deux entiers qui en binaire
s’écrivent [101001100] et [111000]. La plus grande puissance de 2 qui divise
leur pgcd est [100]. Quitte à diviser les deux nombres par [100] on est ramené
au calcul du pgcd de [1010011] et [1110], nécessairement impair. C’est donc le
pgcd de [1010011] et [111], donc celui de la différence [1010011] − [111] et
[111], soit encore [1001100] et [111]. Le pgcd étant toujours impair, on se
ramène à [10011] et [111], etc.
Partant de là, on écrit donc une variante (binaire) de l’algorithme d’Euclide.
Estimer sa complexité dans le pire des cas [8].

 2.2. Développement en fraction continue
L’algorithme d’Euclide, convenablement prolongé aux nombres réels, conduit à une
représentation d’un réel par une suite d’entiers qui fournit également une suite de
rationnels qui converge vers le réel donné. L’approximation rationnelle obtenue est la
meilleure possible.
On part de l’algorithme de division euclidienne que l’on tente d’appliquer
maintenant à deux réels a et b.
Procédure Parties entière et fractionnaire
Entrées : a ≥ 0, b > 0, réels.
Sorties : r, réel, q, entier.
Initialisation : j := 0, α := a
Tant que α ≥ b faire (α, j) ← (α − b, j + 1).

 1. Si la forme de l’algorithme est la même, il y a une différence importante à
noter : il nous faut maintenant disposer d’algorithmes permettant de comparer
deux réels et de les soustraire. Tout dépend des réels que l’on considère et de la
forme sous laquelle on se les donne !
Par exemple, il est simple de comparer\(\sqrt{2}\) et 1 en se ramenant à leurs carrés.
Mais de quelle définition de \(\pi\) part-on pour comparer 3,14159265358979324
et \(\pi\) ? On voit donc que cet algorithme dépend complètement de la structure des
données.

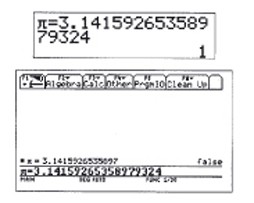
FIG. 2 – Test d’égalité sur une calculatrice numérique du commerce (haut)
et sur une calculatrice symbolique (bas)

 2. Si a > 0 est un réel, la donnée des parties entières des \(a^{10k}\), k ∈ N est
équivalente à la donnée de la suite des approximations décimales de a, elle-même
équivalente à la donnée de \(\alpha\). Le calcul des parties entières des\(a^{10k}\),
k ∈ N peut être vu comme une conversion entre deux façons de donner le réel
\(\alpha\) (l’autre étant par exemple le résultat d’un algorithme, une solution précisée
d’une équation, etc.).
 3. On peut de même imiter l’algorithme d’Euclide de la manière suivante :

Procédure Fraction continue
Entrées : x ≥ 0, réel.
Sorties : \(a_{n}\), n ∈ N, suite d’entiers.
Initialisation : j := 0, \(\alpha\) := x
Tant que \(\alpha \)∉ N faire
\( a_{j}\) := Partie entière \( (\alpha), (\alpha, j)\leftarrow (\frac{1} {\alpha-a_{j}}, j+1\))

On fait les mêmes remarques que pour le calcul des parties entière et
fractionnaire. Ici, l’exécution de la procédure Fraction continue ne s’arrête que
pour les nombres rationnels (le développement en fraction continue de a/b a
pour coefficients les quotients successifs de l’algorithme d’Euclide appliqué à
(a, b)). Pour les autres nombres (voire même pour les rationnels), il faut
préciser à l’avance le nombre de coefficients souhaités. La procédure devient
donc :

Procédure Premiers coefficients du développement en fraction continue
Entrées : x ≥ 0, réel ; N, entier.
Sorties : \(a_{0}\), …, \(a_{n}\), entiers.
Initialisation : j := 0, \(\alpha \) := x
Tant que j ≤ N et α ∉ N faire

\( a_{j}\) := Partie entière \( (\alpha), (\alpha, j)\leftarrow (\frac{1} {\alpha-a_{j}}, j+1\))

Inversement, la donnée d’une suite d’entiers détermine un nombre réel
(indépendamment de toute base de numération).

 4. Un nombre quadratique (i.e. racine d’une équation du second degré à
coefficients entiers) a un développement en fraction continue périodique (au
moins à partir d’un certain rang). Pour en calculer tous les coefficients, il faut
connaître une estimation a priori de la période.

 5. À partir des coefficients du développement en fraction continue, déterminer les
réduites du développement : elles donnent les meilleures approximations
rationnelles du nombre réel.
Un exemple : Jean-Pierre demande à Michel de penser à une fraction dont
numérateur et dénominateur ont (en base 10) trois chiffres chacun et n’ont pas
de facteur commun évident (2, 3, 5). Michel choisit une fraction, détermine le
quotient approché soit 0,3670520231 et le montre à Jean-Pierre qui calcule les
coefficients de son développement en fraction continue :

[0, 2, 1, 2, 1, 1, 1, 2, 3, 1, 390563]
(que penser du dernier de ces coefficients ?)

et les réduites :

\([0, \frac{1}{2}, \frac{1}{3} ,\frac{3}{8}, \frac{4}{11},\frac{7}{19},\frac{11}{30},\frac{29}{79},\frac{98}{267},\frac{127}{346},\frac{49601599}{135135065}]\)

Parmi les réduites Jean-Pierre choisit celle dont les termes ont le bon nombre
de chiffres, et retrouve la fraction 127/346, bien sûr !

On illustre ici la propriété des réduites : une réduite p/q approche x à moins de
\(1/q^{2}\). Il faut donc fournir un quotient approché à moins de \(10^{-7}\) pour avoir une
chance raisonnable. On voit aussi sur l’exemple considéré que la marge est
parfois étroite : 98/267 est aussi une réduite et elle approche le quotient à \(10^{-5}\)
près environ.
Expérimenter et tester la sensibilité à la précision du quotient approché.

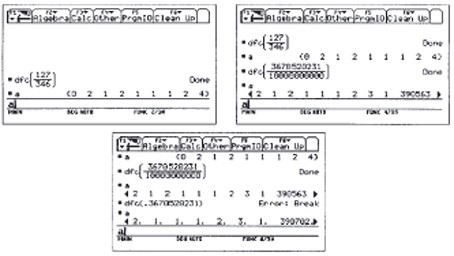
FIG. 3 – Calcul exact (haut). Calcul approché en virgule flottante (bas)

2.3. Arbre de Stern-Brocot

Les fractions irréductibles apparaissent naturellement aux sommets d’un arbre binaire
complet. Les branches infinies de cet arbre représentent les réels.
On part de la liste succinte suivante :

\(\frac{ 0 } {1},\frac{1} {1},\frac{1} {0}\)

En insérant entre deux éléments de cette liste la fraction qui a pour numérateur la
somme des numérateurs et pour dénominateur la somme des dénominateurs, on
conserve l’ordre.

À la première étape, on trouve donc :
\(\frac{0} {1},\frac{1} {2},\frac{1} {1},\frac{2} {1} , \frac{1 } {0 }\)

puis, en recommençant :
\(\frac{0} {1},\frac{1} {3},\frac{1} {2},\frac{2} {3} , \frac{1 } {1 } , \frac{3} {2},\frac{2} {1},\frac{3} {1},\frac{1} {0} , \)

Pour se souvenir de la construction, on décide que chaque fraction est la descendante
des deux fractions entre lesquelles on l’a insérée : elle a ainsi un ancêtre de droite et
un ancêtre de gauche. On doit donc convenir que 1/1 a 0/1 pour ancêtre de gauche et
1/0 pour ancêtre de droite.

L’arbre de Stern-Brocot traduit ces relations de filiation ; ses premières branches,
près de la racine 1/1, sont ainsi disposées :

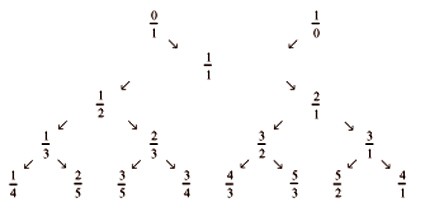
Chaque élément de l’arbre est une fraction dont les coefficients sont les sommes des
coefficients des deux ancêtres les plus proches, l’un à droite et l’autre à gauche.

Pour formaliser la construction :
Si m/n est une fraction à un sommet de l’arbre, son père (ancêtre direct) est soit à
droite, soit à gauche. Une façon de décrire l’arbre est de donner le père de chaque
fraction (le cas de 1/1 est exceptionnel : elle a deux ancêtres que l’on peut considérer
comme directs).
Un nœud n/m a deux fils, l’un à droite, l’autre à gauche, que l’on construit de la
manière suivante : le fils de gauche (resp. de droite) est obtenu en combinant n/m
avec l’ancêtre de gauche (resp. de droite) le plus proche de n/m.

Procédure Parcours de l’arbre de Stern-Brocot. On se donne une suite de directions
gauche (G) ou droite (D) à partir de la racine 1/1 ou d’un autre nœud de l’arbre et on
écrit la liste des fractions rencontrées dans ce parcours.

Remarque : toutes les fractions qui apparaissent aux noœuds de l’arbre sont
irréductibles. Il est très facile de le vérifier : si m′/n′ est un fils de m/n, alors mn′ − m′n = ±1. C’est vrai pour 1/1 et ses deux parents et c’est une propriété
héréditaire. De plus la structure de l’arbre étant compatible avec l’ordre, en deux
nœuds différents figurent des fractions différentes.

Toute fraction irréductible a/b est un nœud de l’arbre : pour le voir, il faut insérer a/b
entre deux éléments de l’arbre de profondeur au plus k. Si la conclusion n’en découle
pas immédiatement, recommencer la comparaison avec les fractions de profondeur
au plus k + 1…

L’arbre de Stern-Brocot est donc un arbre binaire complet dont les nœuds sont les
rationnels positifs.

Procédure Suite de Farey d’ordre N. Écrire la suite ordonnée des fractions
irréductibles inférieures à 1 (par exemple) et de dénominateur au plus égal à N.
On construit le sous-arbre (fini) de l’arbre Stern-Brocot formé des fractions
inférieures à 1 et de dénominateur borné par N. Deux éléments consécutifs
m/n < m′/n′ de cette suite sont toujours tels que m′n − mn′ = 1.
L’arbre de Stern-Brocot est infini. Chacune de ses branches infinies représente un
réel (non rationnel) x dont les meilleures approximations rationnelles sont les nœuds
de la branche considérée. Le lien avec le développement en fraction continue de x est
facile. Inversement, tout réel est associé à une branche de l’arbre, issue de la racine,
finie ou infinie.

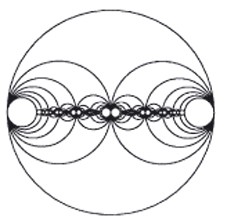
FIG. 4 – Cercles ayant pour diamètres les élements consécutifs de l’arbre de Stern-Brocot
(jusqu’à profondeur 6) : la division récursive de chaque disque
en deux sous-disques reflète la structure binaire de l’arbre,

Noter que les problèmes « métriques » (les irrégularités de distribution visibles sur
la Fig. 4) suscités par ces questions sont liés à l’un des problèmes ouverts les plus
importants des mathématiques, la célèbre Conjecture de Riemann.

3. Jeux de chiffres, un exemple de mathématiques expérimentales

De nombreux logiciels, notamment les systèmes de calcul formel, permettent de
calculer des nombres en grande précision. Il en découle la possibilité d’explorer
expérimentalement certaines propriétés des nombres rationnels ou réels ainsi que de
vérifier concrètement de nombreuses propriétés mathématiques. La réflexion sur
1’expérience suggère souvent en retour de nombreuses questions mathématiques
intéressantes.

3.1. Calculs multi-précision

Demandons à notre petite calculatrice de déterminer \(\alpha=\frac{1} {81}\) . On trouve :

\(\alpha \mapsto 0,01234567\),

et l’apparition successive des chiffres 0, 1, 2, 3, … surprend. Le motif se continue-t-il
 ? Le nombre \(\alpha=\frac{1} {81}\) pourrait-il coïncider avec la constante

C = 0,012345678910111213141516 …

formée de la concaténation des représentations des entiers ? De fait non : tout nombre
rationnel possède un développement décimal qui est ultimement périodique. (Ce fait
s’établit par un peu de réflexion sur le le fonctionnement de l’algorithme de division
enseigné à l’école primaire : les restes partiels dans la division entière \(a\div b\) sont en
nombre borné par b, donc le développement doit « cycler ».) Or la propriété d’ultime
périodicité n’est pas partagée par la constante C (pourquoi ?). Donc, il est avéré que
C est une constante irrationnelle – on l’appelle constante de Champernowne – et en
particulier, que \(\alpha\) ≠ C. D’ailleurs, avec une bonne trentaine de chiffres significatifs,
on trouve

\(\alpha\) = 0.012345679012345679012345679012345 …

Que la représentation de \(\alpha\) contienne les chiffres dans l’ordre, du moins au début,
mérite cependant explication. Qu’y a-t-il de particulier ? Le dénominateur 81 est un
carré, \( 81 = 9^{2}\). Or \(\frac{1} {9} = 0,111111111111111111...\)

On peut donc attaquer le développement décimal de \(\frac{1} {81}\) par l’élévation au carré de
0.1111… Ceci suggère de réfléchir aux produits (donnés par un petit programme
d’une ligne) :

\((11)^{2}= 121\)

\((111)^{2}= 12321\)

\((1111)^{2}= 1234321\)

\((11111)^{2}= 123454321\)

\((111111)^{2}= 12345654321\)

\((1111111)^{2}= 1234567654321\)

\((111111111)^{2}=12345678987654321\)

\((1111111111)^{2}=12345678900987654321\)

\((11111111111)^{2}= 1234567890120987654321\)

\((111111111111)^{2}= 123456789012320987654321\)

Certains motifs apparaissent qui se justifient par une réflexion sur l’algorithme de
multiplication entière (balayage d’un parallélogramme rempli de chiffres 1).
Cependant, le statut des retenues sur de très grands nombres peut être difficile à
gérer.

3.2. Nombres et séries

On peut emprunter une autre voie, moins élémentaire, mais plus fertile. Réexaminons
l’identité :

\(\frac{10} {9}= 1,11111111111111111111...\)
qui se réécrit :

\(\frac{1} {1- \frac{1} {10}} \)=\( 1 +\frac{1} {10}+\frac{1} {10^2}+....\)

Il n’est pas difficile d’y voir une spécialisation de

\(\frac{1} {1- x} =1+x+x^2+x^3+.... \)

obtenue comme limite de la somme d’une progression géométrique finie.

Admettons
qu’on puisse dériver un tel développement. Alors,

\(\frac{1} {{(1- x)}^2} =1+2x+3x^2+4x^3+.... \)

qui donne en \(x = \frac {1} {10}\)

\( \frac{100}{81} = 1 + \frac{2}{10}+ \frac{3}{100 }+ .... +\frac{8}{10^7}+ \frac{9}{10^8}+ \frac{10}{10^9}+ ...\)

et le développement de \(\alpha\) est bien expliqué par quelques majorations élémentaires.
On est passé de l’arithmétique à l’analyse.

Dès lors, sur ce même principe, on peut fabriquer les entiers par tranches de deux
chiffres,

\( \frac{1}{9801} = 0.00 0102 03 04 05 06 07 080910111 21314151617181920 2122 23 24 25 26 27 28 29 30 3132 33 34 35 36 37 38 39\ldots..... \),

ce qui se continue jusque vers la deux-centième décimale (prendre \(x=\frac{1}{100} \)). Ou
encore les puissances de 2 sur tranches de quatre chiffres,

\( \frac{1}{9998}=0.00010002 0004 0008 0016 0032 0064 0128 0256 05121024...\),

voire même les nombres de Fibonacci (1, 1, 2, 3, 5, 8, 13, …), sur tranches de trois
chiffres, par exemple :

\( \frac{1000}{99899}= 0.001 001002 003 005 008 013 021 034 055 089....\),

dont l’explication est instructive.

EXERCICE : Chercher une approximation rationnelle de la constante C de
Champernowne valable avec 3 000 chiffres significatifs mais dont le numérateur et
le dénominateur n’ont pas plus de 20 chiffres ; la vérifier sur ordinateur. (Au delà de
leurs aspects ludiques, de telles approximations servent à établir la transcendance
de C.)

3.3. Rationnels et périodes

On a donc vu que \(\alpha= \frac{1}{81}\) est périodique, la longueur de la période (012345679)
étant 9. Quelle est en général cette longueur ? Par exemple, l’approximation célèbre
du nombre \(\pi\) donne

\( \frac{355} {113}= 3.141592920353982300884955752212389380530973.....\),
sans motif apparent, et l’on ne connaît guère à ce point qu’une borne supérieure de
113 sur la longueur de la période. (En augmentant la précision des calculs on voit
apparaître le motif répété 141592… en les positions 113, 225, 337, etc.).
D’abord, lorsqu’on développe la fraction irréductible a/b, on peut supposer a < b,
puis se débarrasser des facteurs 2 et 5 au dénominateur. Par exemple :

\( \frac{1} {25x17}= \frac{1} {100}x\frac{100} {25}x \frac{1} {17}\)

Donc, à un décalage près (le facteur 1/100), le développement de la fraction est
obtenu en multipliant par 4 (= 100/25) le développement de 1/17. On peut
expérimenter et trouver empiriquement les périodes de diverses fractions. Par
exemple, des longueurs de période sont :

\( \frac{5} {13}\mapsto6\)

\( \frac{8} {13}\mapsto 6\)

\( \frac{9} {17}\mapsto 16\)

\( \frac{13} {17}\mapsto 16\)

\( \frac{6} {19}\mapsto 18\)

\( \frac{4} {21}\mapsto 6\)

On peut multiplier les exemples et tenter d’obtenir un modèle plausible de ce que l’on
observe.

Cette partie donne lieu à divers problèmes de programmation : (i) écrire un
programme qui détermine la longueur de période de 1/b pour b quelconque (ceci doit
partir d’une implantation de l’algorithme de division) ; (ii) tabuler ces valeurs pour b
impair et non multiple de 5 pris dans [3 ; 99] ; (iii) étant donnée une suite de chiffres
de longueur L dont on sait que la période est de longueur au plus m, déterminer cette
période.

Une idée consiste à examiner les valeurs de b qui sont des nombres premiers. Une
seconde idée consiste, à l’inverse, à synthétiser une fraction décimale dont le
développement est connu, comme par exemple

\(0.24681357 24681357....=24681357x 10^{-8}+24681357 x10^{-16}\ldots =24681357 x \frac{1}{ 10^{-8}-1} = \frac {2742373 } { 11111111 }\)

On peut alors faire la jonction avec le « petit » théorème de Fermat et l’ordre
multiplicatif de la base 10 dans le groupe multiplicatif de \( \frac{\mathbb {Z}}{b \mathbb {Z}}\). Il en résulte par
exemple que la longueur de la période est un diviseur de b-1 lorsque b est premier.

À l’arithmétique et l’analyse succède, si l’on veut tirer dans cette direction, un peu
de théorie des groupes élémentaire.

3.4. Ramanujan

Revenons à l’analyse. La question est maintenant de savoir ce que vaut la constante
de Ramanujan :

\(R = \frac {9} {10}.\frac {99} {100}.\frac {999} {1000}\)

(Ramanujan (1887-1920) est un célèbre mathématicien indien autodidacte dont les
découvertes ne cessent d’étonner). La première question qui se pose est celle de
l’existence. Appelons \(R\ _{n}\) le produit obtenu en ne retenant que les n premiers termes.
On trouve :

\(R_{1}= 0.90000000000000000000000000000000000000000000000000\)

\(R_{2}=0.89100000000000000000000000000000000000000000000000\)

\(R_{3}=0.89010900000000000000000000000000000000000000000000\)

\(R_{4}=0.89001998910000000000000000000000000000000000000000\)

\(R_{5}=0.89001108890010900000000000000000000000000000000000\)

\(R_{6}=0.89001019888902009989100000000000000000000000000000\)

\(R_{7}=0.89001010988800021098899001090000000000000000000000\)

\(R_{8}=0.89001010098789911210898790101009989100000000000000\)

\(R_{9}=0.89001010009788901112108878890111198998990010900000\)

Ceci suggère bien que la suite des \(R_{n}\) converge puisque les chiffres se stabilisent. La
preuve par comparaison avec la série géométrique est alors facile et l’on vérifie au
passage que \(R_{n}\) est une approximation correcte jusqu’aux environs du n-ième chiffre.

Dans ces conditions, un système multiprécision nous donne facilement accès aux 100
premiers chiffres de R : il suffit de prendre un peu plus de 100 termes et d’effectuer
les calculs à un peu plus de 100 chiffres significatifs :

\(R=0.890010099998999000000100009999999989999900000000 001000000999999999999899999990000000000000010000000100 00000000\)...

La surprise est que ce nombre ne contient que les chiffres 0, 1, 8, 9.
Quelle peut donc
être la loi ?
L’idée de base est de chercher une représentation par soustraction, en permettant des
chiffres négatifs. Par exemple

\( 0.9 = 1 - \frac{1} { 10} \)

\( 0.89 = 1 - \frac{1} { 10}- \frac{1} { 10^{2}}\)

On trouve alors

\(R = 1 - 10 ^ {-1} - 10 ^ {-2}+10 ^ {-5}+10 ^ {-7} - 10 ^ {-12}- 10 ^ {-15}\)

En fait le nombre R est le cas particulier du produit infini,

\(R(x) = (1 -x) (1-x^{2})(1-x^{3})\)......

pris en \(x =10^{-1}\).

Un petit calcul (à la main ou sous un système de calcul formel)
convainc alors que le produit R(x) développé commence par :

\(1- x-x^{2}+ x^{5}+ x^{7} - x^{12} - x^{15}+x^{22}+ x^{26}..\)

On peut d’ailleurs vérifier numériquement l’hypothèse en évaluant le produit

\(R’ = \frac{99} { 100} x \frac{999} { 1000} x\frac{999 999} { 1000 000}\)

lequel ne comprend encore que les chiffres 0, 1, 8, 9 et correspond à \(R(10^{-2})\). On
pourra en particulier chercher à deviner la loi du développement de R(x).
Nous découvrons ici, par le biais de l’analyse et des calculs multi-précision, un
théorème qui remonte à Euler – le célèbre « théorème pentagonal » –. Les exposants
qui y figurent (1, 2, 5, 7, 12, 15, 22, 26, …) sont connus sous le nom de nombres pentagonaux et sont de la forme \(\frac{1} {2}k(3k\pm1)\).
De fait le théorème pentagonal exprime
l’identité

\(\prod_{j\geq1}(1-x^{j})=1 + \sum_{k\geq1}(-1^{k}) ( x^{\frac{k(3k-1)}{2}} +x^{\frac{k(3k+1)}{2}} )\)

Cette identité est le point de démarrage de la théorie des fonctions elliptiques,
laquelle, après deux siècles d’extrêmes raffinements, a permis à Andrew Wiles de
démontrer en 1994 le « grand » théorème de Fermat.

FIG. 5 – Les systèmes de calcul formel (ici MAPLE)
permettent des calculs tant formels qu’en multi-précision.

La preuve du théorème pentagonal est élémentaire, que ce soit par l’algèbre ou la
combinatoire. (Voir : Louis Comtet, L’analyse combinatoire , P.U.F., Paris, 1970.) La
développer au lycée serait sans doute trop demander. On pourra tout au moins faire
sentir aux élèves que ce théorème met en jeu les propriétés des partitions d’entiers
(ce sont les décompositions additives, du genre 19 = 1 + 1 + 1 + 3 + 5 + 8). Par
exemple, partant d’une réflexion sur la distributivité touchant au sens profond du
développement de

\({(a+b)}^m, {(1+x)}^m, \prod_{j=1}^{n}(1+x^ {j})\)

on se convainc facilement qu’on engendre sous différentes formes tous les choix
possibles parmi m. De là, on voit facilement que les polynômes
engendrent certaines partitions d’entiers en sommants distincts. On peut alors
interpréter les polynômes

\(Q_{m}(x) : =\prod_{j=1}^{m}(1+x^ {j})\)

engendrent certaines partitions d’entiers en sommants distincts. On peut alors
interpréter les polynômes

\(Q’_{m}(x) : =\prod_{j=1}^{m}(1-x^ {j})\)

puis l’énoncé d’Euler en termes de partitions. On pourra observer au passage que
1/R(x) engendre toutes les partitions d’entiers (pour lesquelles il est autorisé de
répéter les sommants).

Les représentations des nombres recèlent bien des secrets. Les mathématiques, même
les plus avancées, ne nous apprennent rien quant au développement décimal de \(\pi\) ou
de\(\sqrt{2}\) . Par exemple, on ne sait exclure actuellement l’hypothèse  [9] qu’à partir d’un
certain rang ces développements ne contiendraient que des chiffres 5 et 6 (!). De
telles propriétés sont cependant hautement improbables puisque ces nombres sont
connus à plusieurs milliards de chiffres (grâce à des algorithmes très astucieux) : tout
indique que, statistiquement, les chiffres qui les composent ont toute l’apparence du
hasard (par exemple, la fréquence de chaque chiffre fluctue autour de \(\frac{1} {10}\)) .

Pour finir sur une note plus positive, voici deux phénomènes curieux, mais bien
expliqués. D’abord la constante de Borwein,

\(B :=4\sum_{k=1}^{500 000} \frac{(-1)^{k-1}} {2k-1}\)

si elle n’approche \(\pi\) qu’au millionième environ (ce qui est attendu), elle partage
néanmoins avec \(\pi\) bon nombre de ses premières décimales :

B = 3.14159065358979324046264338326950288419729139937510305097495

\(\pi\) = 3.14159265358979323846264338327950288419716939937510582097494.

(L’explication fait appel aux propriétés d’approximation des sommes par les
intégrales ; cf. Amer. Math. Monthly, 96 : 8, 1989, p. 681-687.) Sur un tout autre
registre, Ramanujan a découvert la constante

\(e^{\pi\sqrt{163}}= 262537412640768743,9999999999992500725....\),

qui comporte un nombre hautement inhabituel de 9 après la virgule, et est donc
presqu’entière. La justification, par contre, nécessite de l’analyse complexe et de la
théorie des nombres – formes modulaires et réduction des formes quadratiques – qui
sont loin d’être élémentaires (voir J.-P. Serre, Cours d’arithmétique, P.U.F, 1970).

Lire la deuxième partie