Des pavages aux polyèdres de Platon [1]

Une fois encore, nous vous proposons donc des activités expérimentées par nos amis belges,
en les remerciant vivement de nous le permettre.

I. Calcul de l’angle intérieur d’un polygone régulier

1. De quoi a-t-on besoin

Matériel (cf. Annexe) :
Les fiches 28 et 29.

Prérequis :
Les premiers éléments de calcul littéral.
La somme des angles d’un triangle quelconque.

2. Comment s’y prendre

Dans la section précédente, nous nous sommes rendu compte avec des triangles
équilatéraux, des carrés, des hexagones et, a contrario, des pentagones ou des
heptagones, qu’il était nécessaire de connaître les valeurs des angles intérieurs des
polygones réguliers, pour justifier l’existence ou l’inexistence d’un pavage régulier.
Afin d’aller plus loin dans l’étude et, le cas échéant, d’aborder des pavages non
réguliers, le professeur propose aux élèves de calculer les valeurs de ces angles
intérieurs.

Quelle est la valeur de l’angle intérieur d’un polygone régulier à trois côtés ? À quatre côtés ? À cinq côtés ?

Les élèves connaissent bien la valeur de l’angle intérieur d’un polygone régulier à
trois côtés, puisqu’il s’agit du triangle équilatéral dont l’angle vaut 60°. Celui à 4
côtés est le carré, son angle intérieur est connu également : il vaut 90°. Par contre les
élèves ne connaissent pas la valeur de l’angle intérieur du polygone régulier à 5
côtés, le pentagone.

Afin de ne pas s’engager dans des calculs fastidieux propres à chaque polygone, le
professeur propose aux élèves d’établir une formule générale valable quel que soit le
nombre de leurs côtés. Cette formule permettra de déterminer l’angle intérieur d’un
polygone régulier à n côtés.

Pour y arriver, il existe plusieurs méthodes, dont une consiste à décomposer le
polygone régulier en triangles, en partant d’un sommet et en le reliant à tous les
autres sommets qui ne lui sont pas adjacents (figures 19 et 20). Le professeur
distribue la fiche 28 et réalise la démarche avec les élèves.

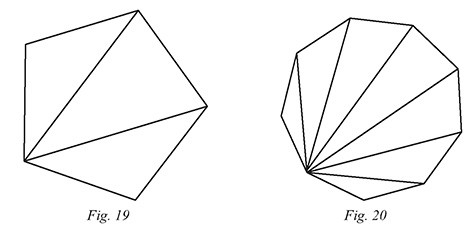
Combien de triangles peut-on ainsi former dans un polygone régulier à n côtés ?

On remarque que le nombre de triangles contenus dans le polygone vaut toujours le
nombre de ses côtés moins 2, on formera donc (n − 2) triangles.

Quel lien existe-t-il entre les angles des triangles et les angles du polygone régulier ?

Si on additionne tous les angles des triangles qui composent le polygone, on obtient
la somme des angles intérieurs de ce dernier. Cette somme vaut donc le produit de
180° par le nombre de triangles. Comme on sait qu’un polygone régulier à n côtés
est composé de (n − 2) triangles, on peut dire que la somme de ses angles vaut
180° × (n − 2).

Somme des angles intérieurs du polygone = (n − 2) × 180°.

Quelle est alors la valeur d’un seul angle intérieur d’un polygone régulier à n côtés ?

Lorsqu’un polygone est régulier, tous ses côtés sont égaux, ainsi que tous ses angles.
La valeur d’un angle vaut donc la somme des angles intérieurs du polygone divisée
par le nombre de ses côtés.

Conclusion : si n est le nombre de côtés d’un polygone régulier, l’angle intérieur a
de ce polygone vaut

$\alpha = \frac{(n-2)x 180}°{n} $

Vérifions, à l’aide de cette formule, qu’il n’y a pas plus de trois pavages réguliers du plan.

Le professeur demande aux élèves de remplacer le n de la formule par le nombre de
côtés du polygone utilisé et d’en déduire $ \alpha $.
Prenons le cas, par exemple, des triangles équilatéraux,

$\alpha = \frac{(3-2)x 180°}{3} = \frac{180°}{3}= 60$°
ce qui correspond bien à la valeur connue des élèves.

Pour les pentagones,

$\alpha = \frac{(5-2)x 180}{5} = \frac{3x180°}{5}= 108$°

Pour former un pavage régulier, il faudrait un nombre entier de pentagones en chaque
nœud. Ce qui veut dire que 108 devrait être diviseur de 360. Or,
3 × 108 = 324 < 360 et 4 × 108 = 432 > 360.
On ne peut donc pas construire de pavage régulier à l’aide de pentagones.
Les valeurs des angles sont répertoriées dans un tableau, dans lequel on fait figurer
le calcul qui permet de déterminer si les polygones peuvent former ou non un pavage
régulier.

n	$\alpha$	somme des angles en un nœud	pavage possible
3	60	6 × 60° = 360°	oui
4	90	4 × 90° = 360°	oui
5	108	3 × 108° < 360°	non
6	120	3 × 120° = 360°	oui
7	128	3 × 128° > 360°	non

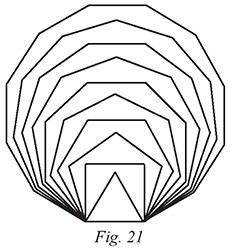
Par l’illustration de la figure 21, le professeur
peut facilement montrer aux élèves que la
valeur de l’angle intérieur d’un polygone ne
cesse d’augmenter avec le nombre de ses
côtés. La démarche est donc bien finie
lorsqu’on a vu que trois fois la valeur de
l’angle d’un heptagone dépasse 360°.

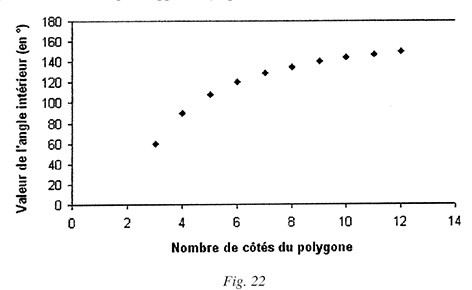
À l’aide de la formule trouvée, le professeur peut proposer aux élèves de construire
le graphe de la valeur de l’angle intérieur du polygone régulier en fonction du
nombre de ses côtés (figure 22). Ce genre de graphe peut être facilement réalisé à
l’aide de l’assistant graphique du tableur Excel. On peut y voir que la courbe est
croissante, que les amplitudes des angles augmentent avec le nombre des côtés et que
cette augmentation est de plus en plus minime. La valeur de l’angle intérieur d’un
polygone régulier à 53 côtés sera de ce fait juste un peu plus grande, à quelques
centièmes de degrés près, que celle d’un polygone régulier à 52 côtés. Le professeur peut également demander aux élèves quelle est la limite de ces amplitudes, et ensuite
de prolonger la suite pour que celle-ci vienne donc « lécher » l’horizontale passant
par l’ordonnée 180 qu’on appelle asymptote.

On peut également montrer algébriquement que si n augmente, alors $\alpha$ augmente.
On a

$}\alpha= 180\frac{n-2}{n}=180x(\frac{n}{n}-\frac{2}{n})= 180x (1-\frac{2}{n}) $

Si n augmente, alors la fraction $\frac{2}{n} $ diminue (car, pour un même numérateur, un
dénominateur plus grand donne une fraction plus petite).

Si la fraction $\frac{2}{n} $ diminue, alors $(1-\frac{2}{n})$ augmente (car on retranche de 1 une
quantité plus petite).

Si $(1-\frac{2}{n})$ augmente, alors $180 x(1-\frac{2}{n})$ augmente (car on multiplie 180° par un
nombre plus grand), donc $\alpha$ augmente.

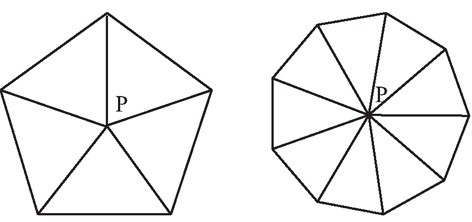
Le professeur peut ensuite proposer aux élèves de déterminer eux-mêmes la
formule à partir d’un autre découpage

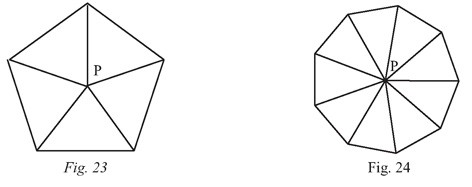
(figures 23 et 24). Il leur distribue la
fiche 29.

Retrouve la formule de l’angle intérieur d’un polygone régulier à partir de cette nouvelle décomposition.

Le professeur laisse les élèves travailler seuls en les guidant de temps en temps si
nécessaire.

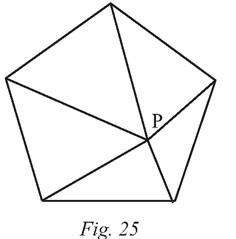
Remarque. – Le point P est ici situé au centre des
polygones afin de faciliter la visualisation. Il faut
cependant être conscient du fait que le raisonnement
est le même pour n’importe quel point P intérieur au
polygone (figure 25).

Les élèves doivent commencer par compter le nombre de triangles obtenus au moyen
de cette découpe. Cette fois, il y a autant de triangles que de côtés du polygone. Il y
aura donc n triangles dans un polygone à n côtés.

Que vaut la somme des angles des triangles ? Correspond-elle encore à la somme des angles intérieurs du polygone ?

La somme des angles des triangles vaut n × 180°.
Mais ici, la somme des angles des triangles ne correspond pas à celle des angles
intérieurs du polygone. En effet, les angles autour du point P, dont la somme vaut
360° puisqu’il s’agit d’un tour complet, sont excédentaires.
Si on additionne tous les angles des triangles, puis qu’on retire les angles en P, on
obtient la somme des angles du polygone. Cela veut dire que l’on doit multiplier 180°
par le nombre de côtes, puis retrancher 360° pour obtenir la somme des angles du
polygone :
n × 180° − 360°.
La valeur d’un seul angle intérieur du polygone vaut alors

$\alpha = \frac{(nx180)-360}{n} $

Cette formule est-elle équivalente à la première ?

Si les élèves n’y pensent pas, le professeur peut leur proposer de mettre 180° en
évidence. Ils obtiennent alors la formule de départ :

$\alpha= \frac{(nx180)-(2x180)}{n}= \frac{180)x(n-2)}{n} $

3. Prolongements possibles

Il est intéressant de montrer aux élèves que la formule de la somme des angles des
polygones réguliers est valable pour tous les polygones convexes quelconques. Par
exemple, si la somme des angles d’un hexagone régulier (figure 26)

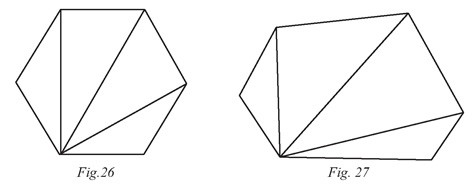
vaut 720°, c’est
également le cas pour l’hexagone quelconque de la figure 27, puisque le découpage
en triangles donne le même résultat.
[La brochure du CREM explore ensuite des pavages semi-réguliers]

4. Échos des classes

La deuxième partie de cette activité se révèle assez difficile pour les élèves. En effet,
ils se focalisent sur la formule trouvée et essaient de s’adapter à la nouvelle
décomposition. Il est alors extrêmement important que le professeur les amène à se
poser les bonnes questions, c’est-à-dire celles qui permettent de mener une démarche
semblable à la première.

Nous proposons donc une fiche détaillée (fiche 30, cf. annexe), sur laquelle se
trouvent des questions intermédiaires. Une de ces questions est : « Que vaut la
somme des angles des triangles ? Correspond-elle encore à la somme des angles
intérieurs du polygone ? ». Cette question est très difficile pour les élèves et nécessite
souvent une explication complémentaire. Voici une proposition qui peut débloquer la
situation en permettant de la visualiser.

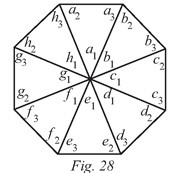
On propose de numéroter (ou de symboliser) les
angles de chaque triangle (figure 28). On demande
aux élèves de dire ce qui va être additionné si on
calcule la somme des angles de tous les triangles.
Ici : $a_1 + a_2 + a_3 + b_1 + b_2 + b_3 + \ldots+ h_1 + h_2 + h_3.$
On demande encore aux élèves si en effectuant ce
calcul on obtient exactement la somme des angles du
polygone. Les élèves se rendent compte qu’on a certains angles en trop, les angles situés au centre, additionnés $a_1 + b_1 + \ldots + h_1$ et
dont la somme vaut 360°.

II. Les polyèdres platoniciens [2]

1. De quoi s’agit-il ?

Les élèves découvrent les cinq polyèdres réguliers par une manipulation.

2. Enjeux

Connaître les cinq polyèdres réguliers et leurs propriétés.

Compétences dans le domaine des mathématiques :
Reconnaître, comparer des solides.
Construire des solides avec du matériel varié.

3. Activité de découverte

De quoi a-t-on besoin ?
Matériel :
Une grande quantité de polygones réguliers en carton, tous à côtés égaux entre eux,
et du papier collant ; ou bien les mallettes de Polydron.

Prérequis :

La séquence précédente.

Comment s’y prendre ?

Le professeur propose aux élèves de repartir d’une tentative de pavage régulier
impossible, au moyen des pentagones.

Comment faire pour assembler trois pentagones ? Comment « supprimer le trou » ?

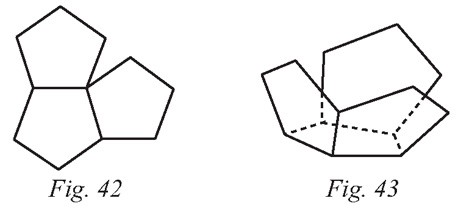
La solution consiste à passer du plan à l’espace. En effet, si on relève les pentagones
autour du nœud, celui-ci devient un sommet et les côtés coïncident alors
parfaitement. La forme obtenue est une sorte de coupelle composée de trois
pentagones autour d’un sommet. On peut alors ajouter un autre pentagone sur un des
côtés (figure 43), et ainsi de suite.

Est-il possible de continuer l’assemblage, de manière à avoir trois pentagones en chaque sommet ?

Les élèves ajustent les pentagones en tenant compte de la consigne. L’assemblage
réalisé semble se refermer ; les élèves construisent en fait un solide dont toutes les
faces sont des pentagones réguliers, qui se réunissent par trois autour de chaque
sommet. Ce solide existe effectivement.

Le professeur demande aux élèves de décrire leur construction.
 « Ce n’est pas un pavage car on ne travaille plus dans le plan, mais dans l’espace. »
 « C’est un volume, un solide. »
 « Il a des faces, des arêtes et des sommets. »
 « Toutes ses faces sont identiques, ce sont des pentagones réguliers. »

Le professeur leur propose d’affiner leur description par une analyse précise des
caractéristiques de ce solide. Il leur demande tout d’abord d’en compter les faces : il
y en a douze. Il leur demande s’ils se souviennent du nom du polygone à douze
côtés : le dodécagone. Il leur explique que le préfixe dodéca vient du grec $\delta\epsilon\kappa\alpha$ - $ \delta\upsilon\o$
qui signifie douze. Il est alors naturel de l’utiliser pour nommer le solide étudié. Le
professeur explique aux élèves que ce solide est particulier. En effet, il est composé
de faces identiques qui sont des polygones réguliers, présentes en même nombre
autour de chaque sommet. On appelle ce genre de solide un polyèdre [3]régulier.

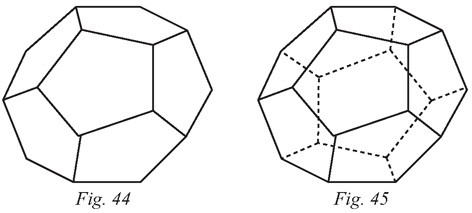
Celui-ci sera donc le dodécaèdre régulier (figures 44 et 45).

Afin de poursuivre l’analyse, le professeur propose aux élèves de déterminer le
nombre d’arêtes et de sommets du dodécaèdre. Pour cela, ils peuvent développer une
stratégie de comptage afin de faciliter le calcul et d’être sûr de ne pas en oublier.

Pour compter le nombre de sommets : on sait que chaque face du dodécaèdre contient
5 sommets (figure 46) et il y a 12 faces. On obtient donc 12 × 5 = 60 sommets. Mais
chaque sommet appartient à 3 faces (figure 47), nous en avons alors compté trois fois
trop. Il faut donc diviser 60 par 3, ce qui nous fait 20 sommets.

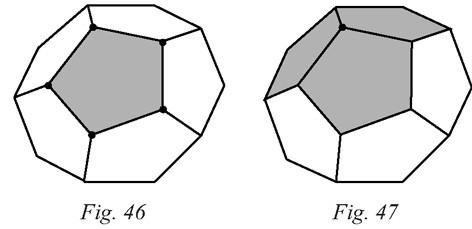
Pour compter le nombre d’arêtes :

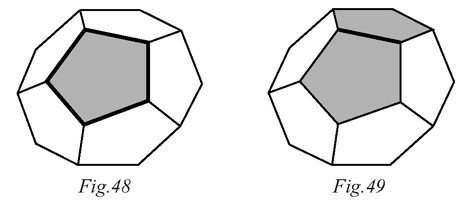
par le même raisonnement, en chaque face, il y a
5 arêtes (figure 48), cela fait donc à nouveau 60 arêtes. Mais chaque arête est
comptée deux fois car elle appartient à 2 faces (figure 49). On divise donc 60 par 2
et on obtient 30 arêtes.

On peut également déterminer le nombre d’arêtes en partant du nombre de sommets,
plutôt que du nombre de faces. On sait qu’il y a 20 sommets. De chaque sommet
partent 3 arêtes

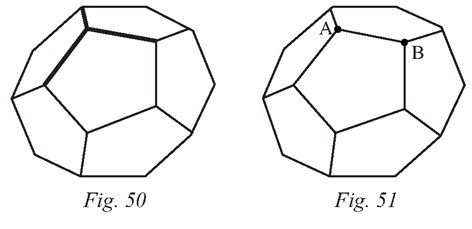
(figure 50), ce qui fait 60 arêtes. Or, les arêtes ont été comptées deux
fois car celle qui part de A vers B est la même que celle qui part de B vers A (figure
51). On divise donc 60 par 2, ce qui nous donne bien 30 arêtes.

Récapitulons : Le dodécaèdre a 12 faces (qui sont des pentagones), 20 sommets et 30
arêtes.

Remarque. — On peut également construire le dodécaèdre

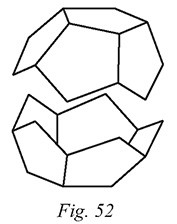
régulier en assemblant deux moitiés de celui-ci, comme le
montre la figure 52. Chaque moitié est facilement obtenue
en assemblant cinq pentagones tout autour d’une « base ».

Essayons de déterminer combien il existe de polyèdres réguliers, à l’aide de la méthode qui vient d’être mise au point.

Pour une meilleure systématisation de l’activité, le professeur propose aux élèves de
commencer par utiliser des triangles équilatéraux, et d’envisager d’en disposer un
certain nombre, le plus petit possible, en chaque sommet du futur solide. Les élèves
se rendent vite compte qu’on ne peut obtenir un volume en n’ayant qu’un seul
polygone en chaque sommet, ni même en n’en ayant que deux. Il faut donc minimum
trois faces pour obtenir un sommet.

En disposant trois triangles équilatéraux autour d’un sommet, les élèves obtiennent
une pyramide, dont ils n’ont plus qu’à refermer la base. Ce qui donne le polyèdre
régulier ci-dessous.

On l’appelle tétraèdre régulier car il a 4 bases (le préfixe tétra vient du grec $\tau\epsilon\tau\rho\alpha$
qui signifie quatre). Le tétraèdre régulier possède 4 faces (qui sont des triangles
équilatéraux), 4 sommets et 6 arêtes.

Afin d’être systématique, le professeur demande aux élèves de réaliser, si possible,
la construction suivante, en disposant non pas trois mais quatre triangles autour d’un
sommet. Les élèves obtiennent à nouveau le « toit » d’une pyramide, à base carrée
cette fois. En complétant les sommets afin qu’ils soient tous composés de quatre
triangles équilatéraux, ils obtiennent un autre polyèdre régulier, qui a huit faces.

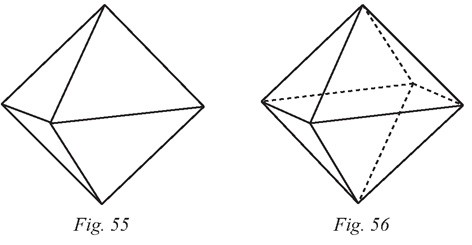
On l’appellera donc l’octaèdre régulier (du grec okta qui signifie
huit).

L’octaèdre régulier possède 8 faces (qui sont des triangles équilatéraux), 6 sommets
et 12 arêtes.

En suivant la même démarche, les élèves assemblent 5 triangles équilatéraux autour
de chaque sommet. Cette construction est plus fastidieuse, le professeur devra donc
être bien attentif et guidera les élèves qui s’embrouillent. Une fois réussie, la
construction donne lieu à un quatrième solide

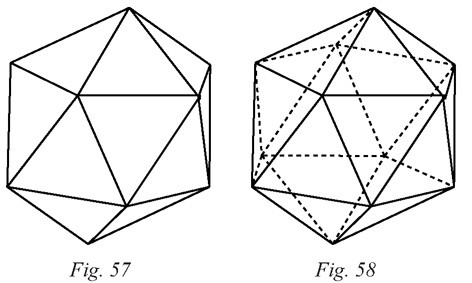
. Celui-ci est
constitué de 20 faces, on l’appellera donc icosaèdre régulier (le préfixe icosa vient
du grec et signifie vingt).

Pour dénombrer les sommets et arêtes, il est à nouveau nécessaire de passer par une
stratégie numérique car, vu la complexité du solide, il est assez difficile de les
compter « à vue ».

Pour les sommets : chaque face possède 3 sommets (figure 59), ce qui donne
3 × 20 = 60 sommets. Or chaque sommet est entouré de 5 faces (figure 60), il faut
donc diviser 60 par 5. On a donc 12 sommets.

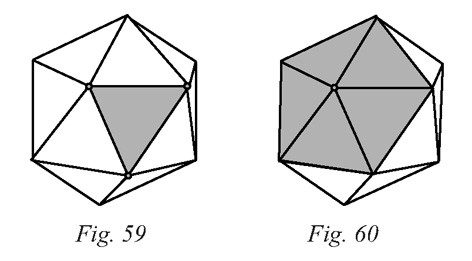
Pour les arêtes : chaque face possède 3 arêtes (figure 61), ce qui fait à nouveau 60
arêtes. Mais chaque arête est comptée deux fois puisqu’elle est commune à deux
faces (figure 62). On a donc 30 arêtes.
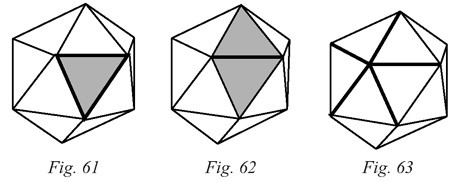
On peut également compter le nombre d’arêtes à partir du nombre de sommets. On
sait qu’il y a 12 sommets, et qu’en chaque sommet il y a 5 arêtes (figure 63). Cela
fait donc 60 arêtes. Or, chaque arête est comptée deux fois, comme expliqué pour le
cas du dodécaèdre (figure 51). On obtient donc bien 30 arêtes.

L’icosaèdre régulier possède 20 faces (qui sont des triangles équilatéraux), 12
sommets et 30 arêtes.

Suivant la logique de l’activité, les élèves essaient de réaliser le prochain solide en
assemblant 6 triangles équilatéraux en chaque sommet. Ils se rendent rapidement
compte qu’ils retrouvent le pavage régulier de triangles. Ils essaient alors avec 7
triangles, mais ne peuvent y arriver car ils se superposent. On a épuisé toutes les
possibilités avec des faces triangulaires. Le professeur propose alors aux élèves
d’essayer avec le « polygone suivant », le carré.
Ils assemblent donc trois carrés en chaque sommet et réalisent le polyèdre régulier le
plus connu, c’est le cube

(figures 64 et 65).

Le cube possède 6 faces (qui sont des carrés), 8 sommets et 12 arêtes.
Essayer de disposer quatre carrés en chaque sommet mène au pavage régulier. Les
élèves n’auront sans doute pas besoin de vérifier que la construction est impossible
avec 5 carrés, car la superposition est immédiate. Il n’y a donc qu’un seul polyèdre
régulier composé de carrés.

Pour poursuivre la démarche, les élèves doivent utiliser maintenant des pentagones.

Or, le polyèdre régulier constitué par l’assemblage de trois pentagones en chaque
sommet a déjà été découvert, tout au début de l’activité. Il s’agissait du dodécaèdre
régulier. Ils essaient alors d’assembler quatre pentagones, mais la construction est
impossible car les polygones se superposent. Ils tentent alors avec des hexagones, et
retrouvent à nouveau le pavage régulier. Ils peuvent encore essayer d’utiliser des
heptagones, mais il n’est même pas possible d’en disposer trois en chaque sommet
sans qu’ils se superposent. À partir de ce moment, il est inutile de continuer, car les
amplitudes des angles intérieurs des polygones réguliers augmentent avec le nombre
de côtés. Il y aura donc toujours une superposition de trois polygones, à partir de
l’heptagone.

On récapitule alors les résultats des constructions.

On a construit cinq polyèdres réguliers [4] qui sont : le tétraèdre, l’octaèdre,
l’icosaèdre, le cube et le dodécaèdre, et nous avons expliqué pourquoi il est
impossible d’en trouver d’autres.

N’est-il pas impressionnant de ne trouver que cinq polyèdres réguliers, alors qu’il y
a une infinité de polygones réguliers ?

Annexe

Fiche 28

Formule de l’angle intérieur d’un polygone régulier (1)

Trouvons ensemble une formule qui permettra de déterminer la valeur de l’angle
intérieur de n’importe quel polygone régulier. Aidons-nous d’une décomposition en
triangles, illustrée ci-dessous pour le pentagone et l’ennéagone.

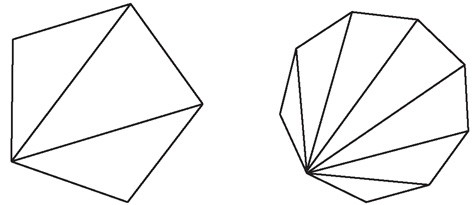
Combien de triangles peut-on ainsi former dans un polygone à n côtés ?

Quel lien existe-t-il entre les angles des triangles et les angles du polygone régulier ?

Quelle est alors la valeur d’un seul angle intérieur d’un polygone régulier à n côtés ?

Fiche 29

Formule de l’angle intérieur d’un polygone régulier (2)

Retrouve la formule de l’angle intérieur d’un polygone régulier à n côtés, à partir de cette nouvelle décomposition.

Fiche 30
Elle reprend les figures et la question ci-dessus avec trois questions supplémentaires :
 Combien de triangles peut-on ainsi former dans un polygone à n côtés ?
 Que vaut la somme des angles des triangles ? Correspond-t-elle encore à la
somme des angles intérieurs du polygone ?
 Quelle est alors la valeur d’un seul angle intérieur d’un polygone régulier à n
côtés ?