Énoncé n° 305

(Pierre DUCHET, 75-Paris)

En appelant « sphinx » et « parallélogramme » les deux formes que voici :

 a) Peut-on paver complètement un triangle équilatéral, de côté n, avec des sphinx ?
 b) Combien peut-on placer (au maximum) de parallélogrammes à l’intérieur d’un
hexagone régulier de côté n ?
Dans les deux cas, les pièces ne doivent pas se recouvrir. Elles peuvent être pivotées
et retournées.

SOLUTION

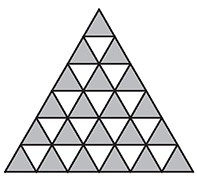
Un triangle \(T_n\), de côté n, \(n^2\) fois plus grand qu’un
triangle unité (de côté 1), contient \(n^2 \) triangles unités,
dont \( 1+2+\ldots+n = \frac{n(n+1)}{2}\) triangles pointes en haut
(orientés dans le même sens que \(T_n\)) et \(\frac{n(n-1)}{2}\)
triangles pointes en bas (orientés différemment).

Or chaque sphinx couvre 6 triangles unités, dont 4 orientés dans un sens et 2 orientés
dans l’autre. Pour que \(T_n\) soit pavable par des sphinx, non seulement \(n^2\) doit être
multiple de 6, soit n = 6k, mais \( \frac{n(n+1)}{2} = 3k(6k+1)\) doit être pair, donc k lui aussi
pair. Il est donc nécessaire que n soit multiple de 12, et réciproquement, si n est
multiple de 12, \(T_n\) étant pavable par des triangles \(T_{12}\), il suffit de trouver un pavage
du triangle \(T_{12}\) pour prouver que cette condition nécessaire est aussi suffisante.

Pierre Duchet et moi tenions le stand commun MATh.en.JEANS - Animath lorsqu’il
m’a soumis ce problème. Les élèves qui l’ont cherché ont compté le nombre de
triangles unités, dans des cas particuliers, sans remarquer que \(T_n\) était \(n^2}\) fois plus
grand qu’un triangle unité. La difficulté était le cas n = 6 ; un père a dit à son fils
d’une dizaine d’années : « on ne bouge pas d’ici tant que tu n’as pas trouvé ».
Pour
n = 12, Pierre Jullien et Pierre Bornsztein proposent le même pavage, invariant par
rotation de 120°, mais Michel Lafond en trouve un autre.

Les problèmes de pavage sont généralement solubles par des coloriages. Pour cette
première question, on n’avait guère le choix, les trois solutions justes reçues sont
identiques. Mais pour la seconde question, Pierre Bornsztein et moi proposons des
solutions en noir et blanc (pardon : en rouge et bleu pour Pierre Bornsztein) alors que
Michel Lafond et Pierre Jullien préfèrent la quadrichromie.

Il est clair pour tout le monde que, le quadrilatère
couvrant quatre triangles alors que l’hexagone de côté n
(réunion de 6 triangles équilatéraux de côté n) en couvre
\(6n^2\), le pavage de tout l’hexagone n’est possible que si n
est pair : en divisant l’hexagone en trois losanges (qui
peuvent être vus comme trois faces d’un cube en
perspective), il est facile de réaliser un pavage dans ce
cas. Lorsque n est impair, \(6n^2\) n’étant pas divisible par 4,
au moins deux cases (triangles unités) ne seront pas
couvertes, et tout le problème consiste à prouver qu’en
réalité, 6 cases au moins ne seront pas couvertes.

Pierre Bornsztein distingue trois types de
parallélogrammes, 1, 2 et 3 selon que leur grand côté est
parallèle à l’une des trois grandes diagonales \(D_1\), \(D_2\) et
\(D_3\).

Comme les nombres \(k_1\), \(k_2\) et \(k_3\) de parallélogrammes
de chaque type ne peuvent pas être de trois parités
distinctes, on peut supposer, par exemple, que \(k_1\) et \(k_3\)
sont de même parité. On découpe alors l’hexagone en
bandes parallèles à \(D_2\)
, larges d’une case,
alternativement bleues et rouges : ces bandes
s’échangent par symétrie par rapport à \(D_2\), il y a donc
\(3n^2\) cases bleues et \(3n^2\) cases rouges. Chaque
parallélogramme de type 1 ou 3 couvre obligatoirement
deux cases rouges et deux cases bleues, donc ces deux types réunis couvrent \(2(k_1 + k_3)\) cases rouges et autant de
cases bleues : comme \(k_1\) et \(k_3\) sont de même parité,
\(2(k_1 + k_3)\) est multiple de 4. Chaque parallélogramme de
type 2 couvre soit quatre cases rouges, soit quatre cases
bleues. Donc le nombre de cases rouges couvertes par
l’ensemble des parallélogrammes est multiple de 4, et
comme \(3n^2\) est congru à 3 modulo 4, il y a au moins 3
cases rouges non couvertes. De même, il y a au moins 3
cases bleues non couvertes, donc en tout 6 cases au
moins non couvertes.

Trouver un pavage de l’hexagone moins 6 cases n’est
pas difficile : si n = 2k + 1, on peut isoler un hexagone
central H de côté 1 (non couvert) et diviser le reste en
trois bandes de grand côté 2k et trois losanges de côtés
2k et (2k + 1), facilement pavables. Appelons P ce
pavage.

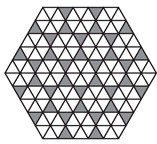
L’autre approche du problème, assez différente,
fait appel au coloriage que voici. Comme dans
toute bande (large d’une case) parallèle à une
grande diagonale, une case sur quatre est noire,
chaque parallélogramme (nécessairement inclus
dans une telle bande) contient une et une seule
case noire : il y a donc autant de cases noires
couvertes que de parallélogrammes. Or le pavage
P couvre toutes les cases noires : on ne peut pas
en couvrir davantage, donc on ne peut pas placer
davantage de parallélogrammes, d’où, en
définitive, on ne peut pas couvrir davantage de
cases. Quel que soit le pavage, 6 cases au moins
seront non couvertes.

J’étais très fier de cette démonstration jusqu’à ce que
Pierre Jullien et Michel Lafond en proposent une très
voisine, mais en quadrichromie. Le coloriage ci-contre
– obtenu en faisant basculer, proprement mais dans tous
les sens, sur notre triangulation de l’hexagone un
tampon encreur tétraédrique – est tel que le
parallélogramme (qui est un patron plan du tétraèdre),
quelle que soit sa position, couvre une case de chaque
couleur. Le pavage P prouve que dans l’hexagone de
côté n privé de H (les six cases centrales), il y a autant
de cases de chaque couleur. Comme une couleur n’est pas présente dans H,
l’hexagone contient \(\frac{6n^{2}-6}{4}\) cases de cette couleur et \(\frac{6n^{2}+2}{4}\) cases de chacune des trois autres couleurs.

Quel que soit le pavage, celui-ci couvre donc au plus \((6n^{2}- 6)\)
cases.

Ces deux dernières démonstrations s’appliquent au pavage de l’hexagone régulier de
côté 2k + 1 par des triangles équilatéraux de côté 2 : au moins 6 cases seront non
couvertes. Mais dans ce dernier cas, existe-t-il des pavages où moins de 14 cases sont
non couvertes ?