Par Gilles Dowek [1]

1. Une histoire avec deux portes

Toute cette histoire s’est déroulée dans une petite pièce, dans laquelle on pouvait
entrer et sortir par deux portes, chacune ouverte et fermée par un portier. Les portiers
devaient veiller à ce que les deux portes ne soient jamais ouvertes en même temps,
car cette petite pièce était le sas d’un vaisseau spatial pressurisé, qui se serait
instantanément vidé de son air si les deux portes avaient été simultanément ouvertes.

• 1.1. Les vaisseaux de première génération
  Dans la première génération de vaisseaux, chaque portier, avant d’ouvrir sa porte,
  vérifiait que l’autre porte était fermée.
  Hélas, un jour, les deux portiers ont vérifié au même moment que l’autre porte
  était fermée, puis ils ont ouvert chacun sa porte et les passagers du vaisseau ont été
  aspirés dans le vide intersidéral. En fait, il n’est même pas certain que les deux
  portiers aient effectué leur vérification exactement au même moment, ce qui serait
  vraiment un manque de chance incroyable, car il se passait toujours deux ou trois
  secondes entre le moment où un portier vérifiait l’autre porte et ouvrait la sienne. Il
  a suffit que l’autre portier effectue sa vérification pendant cette courte durée, pour
  qu’il se soit cru, lui aussi, autorisé à ouvrir sa porte.
• 1.2. Les vaisseaux de deuxième génération
  Dans une deuxième génération de vaisseaux, le protocole avait été amélioré : à
  coté de chaque porte, on avait mis un drapeau rouge que le portier devait hisser avant
  d’ouvrir sa porte et qu’il ne pouvait baisser qu’après l’avoir refermée et, une fois son
  drapeau hissé, il ne pouvait ouvrir sa porte, qu’après avoir vérifié que le drapeau de
  l’autre porte était baissé.
  Mais après les déboires de la première génération de vaisseaux, dus au fait que
  ses concepteurs s’étaient laissé abuser par de fausses évidences : ben oui, s’étaient -ils
  dit, si chaque portier vérifie l’autre porte avant d’ouvrir la sienne, il ne pourra
  jamais arriver que les deux portes soient ouvertes en même temps, il fallait
  maintenant atteindre une véritable certitude de la sûreté du nouveau protocole : une
  certitude mathématique.
  Dans les vaisseaux de la première génération, la vie d’un portier n’était jamais
  ennuyeuse, mais elle était très simple : il passait ses journées à ouvrir et fermer sa
  porte. Un portier ne pouvait donc être que dans deux états mentaux : il était dans l’état 0 quand sa porte était fermée et dans l’état 1 quand sa porte était ouverte. Il
  passait continuellement de l’état 0 à l’état 1 (à condition que l’autre portier soit dans
  l’état 0) et de l’état 1 à l’état 0. Les deux portiers, pris ensembles, pouvait être dans
  quatre états mentaux différents (0,0) : les deux portes fermées, (0,1) : la porte d’Alice
  fermée, la porte de Bob ouverte, (1,0) : la porte d’Alice ouverte, la porte de Bob
  fermée et (1,1) : les deux portes ouvertes (on a oublié de vous le dire : les deux
  portiers s’appelaient Alice et Bob, comme tout le monde).
  Quand les portiers étaient dans l’état (0,0), ils pouvaient évoluer vers l’état (1,0)
  (Alice pouvait ouvrir sa porte puisque celle de Bob était fermée) et, symétriquement,
  vers l’état (0,1). Quand ils étaient dans l’état (1,0), ils pouvaient évoluer vers l’état
  (0,0) (Alice fermait sa porte), mais pas vers l’état (1,1) (la porte d’Alice étant
  ouverte, Bob ne pouvait pas ouvrir la sienne). Symétriquement, quand ils étaient dans
  l’état (0,1), ils pouvaient évoluer vers l’état (0,0), mais pas vers l’état (1,1). Si jamais
  ils s’étaient retrouvés dans l’état (1,1), ils auraient pu évoluer vers les états (0,1) et
  (1,0) (puisque chacun des portiers pouvait fermer sa porte). Mais, comme nous
  l’avons vu, il était également possible que les deux portiers agissent en même temps,
  ce qui ajoutait la funeste transition de (0,0) vers (1,1) (ainsi qu’une transition de (1,1)
  vers (0,0)). Finalement, le graphe des transitions était celui-ci :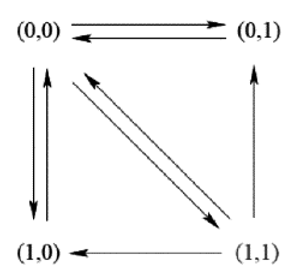

  

  Et, du fait de la transition de l’état (0,0) vers l’état (1,1) (la flèche diagonale
  orientée vers le bas et la droite sur le dessin), il était possible d’évoluer de l’état
  initial (0,0) vers l’état fatal (1,1).
  Dans les vaisseaux de la deuxième génération, un portier pouvait être dans quatre
  états mentaux différents : dans l’état 0 son drapeau était baissé et sa porte était
  fermée, dans l’état 1 son drapeau était hissé mais sa porte était toujours fermée, dans
  l’état 2 son drapeau était hissé et sa porte était ouverte, dans l’état 3 son drapeau était
  encore hissé mais sa porte était refermée. Chaque portier passait donc de l’état 0 à
  l’état 1, puis de l’état 1 à l’état 2 (à condition que le drapeau de l’autre portier soit
  baissé, c’est-à-dire que l’autre portier soit dans l’état 0), puis de l’état 2 à l’état 3 et
  enfin de l’état 3 à l’état 0.
  En observant uniquement le drapeau et la porte, il était impossible de distinguer
  l’état 1 de l’état 3 (dans les deux cas le drapeau était hissé et la porte était fermée).
  Mais le portier, qui avait bonne mémoire, savait s’il venait de hisser son drapeau ou
  de refermer sa porte. Et s’il venait de hisser son drapeau, le protocole ne prévoyait
  pas qu’il puisse le baisser sans avoir d’abord ouvert puis refermé sa porte.
  Dans ce deuxième protocole, le graphe des transitions était celui-ci :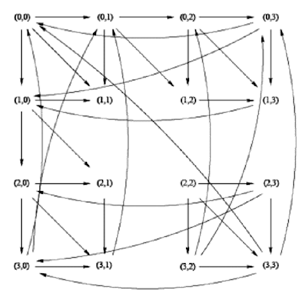

  

  
  Ce graphe comportait seize états et trente sept transitions : de chaque état,
  partaient trois flèches, l’une vers la droite, l’autre vers le bas et la troisième en
  diagonale vers le bas et la droite, sauf dans les onze cas où la transition correspondait
  à une transition de 1 vers 2 pour l’un des portiers, alors que l’autre était dans l’état
  1, 2 ou 3 au départ.
  Dans ce graphe, aucune flèche n’avait pour extrémité l’état fatal (2,2) dans lequel
  les deux portes sont ouvertes. De ce fait, il n’y avait pas de chemin qui menait de
  l’état initial (0,0) à l’état fatal (2,2). Contrairement aux vaisseaux de la première
  génération, il n’y avait donc pas de scénario dans lequel les deux portiers respectaient
  le protocole et dans lequel les deux portes finissaient par être ouvertes en même
  temps.
  Dans ce cas, il était simple de calculer toutes les transitions et de dessiner le
  graphe, ce qui permettait de constater qu’il n’y a pas de transition qui menait à l’état
  (2,2). Mais, au lieu de calculer, on pouvait préférer raisonner : une transition qui
  aurait mené à l’état (2,2), aurait dû partir de l’un des états (1,2), (2,1) et (1,1) et
  aucune de ces trois transitions n’était autorisée par le protocole, puisque l’un au
  moins des portiers effectuait une transition de l’état 1 vers l’état 2, alors que l’autre
  était dans l’état 1 ou dans l’état 2 au départ.
  Ce protocole était donc sûr, cela était mathématiquement démontré.
  Un jour
  cependant, le vaisseau revint sur Terre sans avoir eu d’accident (sa sûreté n’était donc
  pas mise en défaut), mais aussi sans avoir pu effectuer sa mission.
  Que s’était-il
  passé ?
  Il s’était passé que, à nouveau, les deux portiers avaient tenté d’ouvrir leur porte
  au même moment. Ils avaient alors l’un et l’autre hissé leur drapeau, puis chacun
  avait attendu que l’autre veuille bien baisser son drapeau pour pouvoir ouvrir la
  porte, mais en vain.
  

Cette situation de blocage est visible sur le graphe des transitions : il y a un
chemin qui va de l’état initial (0,0) vers l’état (1,1) (par exemple, en passant par
(1,0)), mais une fois cet état atteint, il n’y a plus de transition possible. Il fallut donc
concevoir une troisième génération de vaisseaux, avec encore un autre protocole.

• 1.3. Les vaisseaux de troisième génération
  Dans ce nouveau protocole, on utilise en plus des deux drapeaux, un témoin, tel
  ceux qu’utilisent les athlètes lors d’un relais. Après avoir hissé son drapeau et avant
  d’ouvrir sa porte, chaque portier doit céder le témoin à l’autre portier, c’est-à-dire lui
  lancer le témoin à travers le sas, si jamais il a le témoin en main, et ne rien faire sinon
  (dans le cas où chacun des portiers cède le témoin à l’autre au même moment, le
  témoin peut se retrouver aussi bien chez l’un que chez l’autre portier).
  Ensuite, un
  portier peut ouvrir sa porte, si le drapeau de l’autre portier est baissé, mais aussi s’il
  a le témoin en main. On comprend le rôle de ce témoin : dans la situation de blocage
  où les deux drapeaux sont hissés, l’un des portiers a désormais le témoin en main et
  peut donc ouvrir sa porte, débloquant la situation.
  Un portier passe donc désormais non plus par deux ou quatre états mentaux
  différents, mais par cinq : dans l’état 0 son drapeau est baissé et sa porte est fermée,
  dans l’état 1 son drapeau est hissé, sa porte est toujours fermée et il n’a pas encore
  cédé le témoin, dans l’état 2 son drapeau est hissé, sa porte est toujours fermée, mais
  il a cédé le témoin, dans l’état 3 son drapeau est hissé et sa porte est ouverte, dans
  l’état 4 son drapeau est hissé et sa porte est refermée.
  Chaque portier passe donc de l’état 0 à l’état 1, puis de l’état 1 à l’état 2, puis de
  l’état 2 à l’état 3 (à condition qu’il ait le témoin en main ou que le drapeau de l’autre
  portier soit baissé, c’est-à-dire que l’autre portier soit dans l’état 0), puis de l’état 3
  à l’état 4, en enfin de l’état 4 à l’état 0.
  

Le graphe des états de ce protocole est un peu plus gros, d’une part, parce que
chacun des portiers peut désormais être dans cinq états mentaux différents et non
quatre, mais aussi parce qu’il faut ajouter dans la description de l’état global, le nom
du portier qui a le témoin en main. Si bien qu’il y a cinquante états possibles. On peut
continuer à calculer les transitions et constater que les états fatals (3,3, Alice) et (3,3,
Bob) ne sont pas accessibles depuis les états initiaux (0,0, Alice) et (0,0, Bob). Il vaut
mieux cependant éviter de faire ce calcul à la main, d’une part parce qu’il est un peu
pénible, d’autre part parce qu’il est très difficile de ne pas faire d’erreurs quand on
effectue un calcul aussi répétitif. Mais, au lieu d’effectuer ce calcul, on peut aussi
construire le raisonnement suivant.
Une transition qui mène à l’état (3,3, Alice) peut partir de six états différents :
(2,3, Alice), (2,3, Bob), (3,2, Alice), (3,2, Bob), (2,2, Alice) et (2,2, Bob).
Parmi ces
six transitions, une seule est permise par le protocole : celle qui part de l’état (2,3,
Alice). En effet, celles qui partent des états (2,3, Bob), (3,2, Bob) et (2,2, Bob) sont
impossibles, car le témoin ne peut passer de Bob à Alice que si Bob effectue une
transition de 1 à 2, ce qui n’est pas le cas. Celles qui partent des états (3,2, Alice) et
(2,2, Alice) sont impossibles, car Alice n’étant pas dans l’état 0 et Bob n’ayant pas le
témoin en main, Bob ne peut pas ouvrir la porte.
Pour montrer qu’il n’y a pas de chemin dans le graphe qui mène d’un état initial
à l’état (3,3, Alice), il faut donc montrer, préalablement, qu’il n’y a pas de chemin qui mène d’un état initial à l’état (2,3, Alice). On montre pour cela qu’il n’y a pas de
transition qui mène à cet état. À nouveau, une transition qui mène à l’état (2,3, Alice)
peut partir de six états différents : (1,3, Alice), (1,3, Bob), (2,2, Alice), (2,2, Bob),
(1,2, Alice) et (1,2, Bob). Les transitions qui partent des états (1,3, Alice), (1,3, Bob),
(1,2, Alice) et (1,2, Bob) sont impossibles, car Alice cédant le témoin, et Bob ne le
cédant pas, c’est Bob et non Alice qui devrait avoir le témoin à la fin de la transition.
De même, celle qui part de l’état (2,2, Bob) est impossible car Bob ayant le témoin
en main et ne le cédant pas, c’est Bob et non Alice qui devrait l’avoir à la fin de la
transition. Enfin, celle qui part de l’état (2,2, Alice) est impossible car Bob ne peut
pas ouvrir la porte s’il n’a pas le témoin en main et que le drapeau d’Alice est hissé.
Il n’y a donc pas de chemin dans le graphe qui mène d’un état initial à l’état fatal
(3,3, Alice) et, de manière symétrique, il n’y a pas de chemin qui mène d’un état
initial à l’état (3,3, Bob).

Ce protocole, comme celui des vaisseaux de la deuxième génération, est sûr. On
peut montrer également que, contrairement au protocole des vaisseaux de la
deuxième génération, il ne présente pas de situation de blocage, dans laquelle aucun
des portier ne peut agir, et, de plus, que dans n’importe quelle situation, un portier
qui souhaite ouvrir sa porte finira toujours par pouvoir le faire.

2. La morale de l’histoire

Cette histoire vient d’un problème qui s’appelle le problème de l’exclusion
mutuelle et qui consiste à synchroniser deux processus, de manière à ce qu’ils ne
puissent pas être simultanément dans un certain état critique (dans notre exemple que
les portiers ne puissent pas l’un et l’autre avoir leur porte ouverte).

Un exemple plus
banal que cette histoire de vaisseaux spatiaux est celui de l’accès à une imprimante
partagée par un réseau d’ordinateurs : il ne faut pas que deux ordinateurs utilisent
l’imprimante en même temps, ce qui mènerait, au mieux, à mélanger les pages des
documents imprimés. De même, deux opérations de mise à jour d’un compte en
banque, qui consistent chacune à lire la valeur c du compte dans une base de données,
à ajouter une certaine valeur (x dans le premier cas et y dans le second), à cette valeur
c et à remplacer dans la base de données la valeur c par le résultat de cette addition,
doivent être mutuellement exclusives, si on veut être certain d’obtenir le résultat
c + x + y, et non c + x ou c + y, à la fin du calcul.

S’il est assez facile de trouver des protocoles qui garantissent l’exclusion
mutuelle de deux processus, comme le montre le deuxième protocole de l’histoire, il
est plus difficile de garantir en même temps l’absence de blocage et le fait que
chacun des processus puisse progresser. Ce problème n’a en fait été complètement
résolu qu’en 1981 par Peterson qui a proposé le troisième protocole de notre histoire.
(voir, par exemple : http://en.wikipedia.org/wiki/Peterson’s_algorithm).

Toutefois, malgré son importance en algorithmique distribuée, l’algorithme de
Peterson n’est pas, en lui-même, ce qui motive cette histoire. Ce qu’elle cherche,
avant tout, à illustrer est le fait que quand on veut comprendre un système (par
exemple, le protocole utilisé dans la première génération de vaisseaux, où, nous dit
on, « chaque portier, avant d’ouvrir sa porte, vérifiait que l’autre porte était
fermée  »), il faut se méfier des fausses évidences et chercher le degré de certitude que
donne la démonstration mathématique.

De même que pour démontrer des propriétés d’un système physique, par exemple
une masselotte oscillant au bout d’un ressort, il est, dans un premier temps,
nécessaire de le mathématiser, par exemple sous la forme de l’équation différentielle

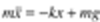
pour démontrer des propriétés d’un protocole comme celui-ci, il faut
commencer par le mathématiser. Toutefois, à la différence de la masselotte au bout
de son ressort, ce protocole ne se laisse pas mathématiser sous la forme d’une
équation différentielle. Le bon avatar mathématique de ce protocole n’est pas une
équation différentielle, mais un algorithme : l’algorithme qui, à chaque état, associe
un ensemble de transitions vers d’autres états.

Depuis la révolution galiléenne, au début du XVIIe siècle, les mathématiques ont
beaucoup montré leur pertinence pour étudier les systèmes physiques, la plupart du
temps mathématisés sous la forme d’équations différentielles (les équations de
Newton, les équations de Maxwell, …) et la grande métamorphose des sciences au
XXe et XXIe siècle est peut-être que cette révolution galiléenne s’est étendue à de
nombreux autres domaines, par exemple, de nombreuses régions de la biologie et des
sciences humaines, qui sont aujourd’hui aussi mathématisées que la physique. Mais,
à la différence des objets de la physique, les objets de la biologie (tels les processus
cellulaires) ou des sciences humaines (telles les grammaires des langues naturelles)
se sont davantage laissé mathématiser sous la forme d’algorithmes, que sous la forme
d’équations différentielles.

Cette diversification des outils permettant de mathématiser les objets étudiés par
la physique, la biologie, les sciences humaines et les objets techniques que nous
construisons (par exemple, les protocoles d’ouverture et de fermeture des portes d’un
vaisseau spatial ou les protocoles d’utilisation d’un réseau ferré ou aérien) fait que le
talent mathématique qui est aujourd’hui attendu de nos élèves est souvent celui de
savoir formuler un problème en termes mathématiques, d’aborder en mathématicien
non seulement les problèmes de thermodynamique que pose la conception du moteur
d’une locomotive, mais aussi les problèmes de logistique que pose l’organisation
d’un réseau de tramways.
Mathématiser (formaliser, modéliser, …, tous ces verbes sont synonymes) les
trois protocoles d’ouverture et de fermeture des portes du vaisseau spatial de cette
histoire n’est pas complètement immédiat. Tout d’abord, dans le deuxième protocole,
nous avons choisi de décrire l’état de chacun des portiers en considérant non pas
l’état de la porte (ouverte ou fermée) et du drapeau (hissé ou baissé), mais l’état
mental du portier. Ce qui nous a mené à distinguer deux états dans lesquels le portier
a hissé le drapeau mais pas encore ouvert la porte et celui dans lequel il a refermé la
porte, mais pas encore baissé le drapeau, bien que dans les deux cas, le drapeau soit
hissé et la porte fermée. Il est également possible de confondre ces deux états. On
obtient alors une description moins précise quoiqu’exacte du protocole. Cela revient
à imaginer un protocole un peu plus libéral, dans lequel un portier après avoir hissé
son drapeau peut le baisser sans ouvrir et refermer sa porte. Ce protocole plus libéral
est sûr également (identifier les états 0 et 3 dans le graphe ci-avant ne change rien au
fait qu’il n’y a aucune transition qui aboutit à l’état fatal (2,2)). Ce protocole plus
libéral est donc sûr, et c’est a fortiori le cas du protocole plus contraint.
On pourrait, de même, dans le troisième protocole, ignorer le nom du portier qui
a le témoin en main. On obtiendrait alors une autre description moins précise
quoiqu’encore exacte du protocole. Cela revient à nouveau à imaginer un protocole
plus libéral, dans lequel les portiers peuvent se céder le témoin à n’importe quel
moment. Cette description du protocole n’est cependant pas assez précise pour en
établir la sûreté puisqu’il y a un chemin qui mène de l’état initial (0,0,A) à l’état fatal
(3,3,A) :

\((0,0,A)\rightarrow (0,1,A) \rightarrow(0,2,A) \rightarrow (1,2,A) \rightarrow(2,2,B) \rightarrow (2,3,B) \rightarrow (2,3,A) \rightarrow(3,3,A) \).

Comme dans la description mathématique d’une masselotte au bout d’un ressort,
on a le choix d’inclure ou d’ignorer un certain nombre de détails. Mais une
description trop lacunaire ne permet plus de démontrer les propriétés que l’on
souhaite établir.
Une autre question concerne la manière dont les actions des portiers s’inscrivent
dans le temps physique. Dans certains cas, on veut qu’à chaque unité de temps, tous
les processus effectuent simultanément une transition. On dit alors que les processus
partagent la même horloge ou qu’ils sont synchrones. C’est, par exemple, le cas des
musiciens d’un orchestre. Dans d’autres cas, comme dans celui de notre histoire,
chaque processus va à son propre tempo et peut rester un temps arbitraire dans un
certain état avant d’effectuer une transition. On dit alors que les processus sont
asynchrones.
Si, dans l’état 0, les deux portiers peuvent effectuer une unique transition vers un
état 1, l’unique transition possible depuis l’état (0,0), pour l’ensemble des portiers,
dans le cas synchrone, est vers l’état (1,1). Dans le cas asynchrone, en revanche, il y
a deux transitions de plus vers les états (1,0) et (0,1), dans lesquelles l’un des portiers
effectue une transition et l’autre non. Toutefois, la première transition vers l’état (1,1)
continue d’être une transition possible et c’est son oubli qui avait laissé croire que le
premier protocole de l’histoire était sûr.
Envisager le cas de transitions simultanées dans le premier protocole est d’autant
plus nécessaire que ce cas a une probabilité non nulle de se produire.
En effet, pour
chacun des portiers, on considère comme une transition unique à la fois la
vérification de l’autre porte et l’ouverture de sa propre porte. Il devient alors délicat
de supposer qu’une telle transition soit instantanée. Mais garantir que deux
transitions ayant chacune une certaine durée ont lieu l’une après l’autre (c’est-a-dire
interdire ici aux deux portiers d’agir simultanément) nécessite de recourir à un
protocole d’exclusion mutuelle, ce qui serait circulaire.
On devrait, en toute rigueur, considérer également le cas dans lequel un portier
effectue une transition pendant que l’autre en effectue deux ou davantage. Mais on
peut éviter de le faire, en faisant quelques hypothèses sur la manière dont les actions
des portiers, formalisées par des transitions d’un état à un autre, se déroulent dans le
temps physique. Par exemple, si on suppose que chacune de ces actions se déroule
en moins de cinq secondes et que chaque portier attend au moins dix secondes entre
deux actions, il est facile de se convaincre qu’il est nécessaire de considérer les cas
dans lesquels les portiers effectuent simultanément une transition, mais pas ceux
dans lesquels un portier effectue une transition pendant que l’autre en effectue deux
ou davantage.
Dans la résolution d’un problème de mécanique comme celui de la détermination
de la période des oscillations d’une masselotte au bout d’un ressort, la difficulté n’est
pas dans la mathématisation du problème : le système est décrit en de tels termes que
passer de sa description à l’équation différentielle est quasiment
immédiat. La partie difficile est plutôt dans la résolution de cette équation. En
revanche, dans l’analyse d’un objet comme les protocoles d’ouverture et de
fermeture des portes décrits dans cette histoire, c’est la mathématisation du problème
qui est difficile. Le problème, une fois mathématiquement bien posé, est quasiment
résolu. Il n’y a pas que démontrer des théorèmes qui soit difficile en mathématiques,
trouver les bonnes définitions l’est tout autant.

Cette histoire nous montre enfin à quoi pourrait ressembler un exercice de
mathématiques, quand la notion d’algorithme sera pleinement enseignée. La
première étape d’un tel enseignement à laquelle on pense est l’enseignement des
algorithmes mathématiques fondamentaux : le triangle de Pascal, le pivot de Gauss,
…
La deuxième est l’éveil à la sensibilité du caractère algorithmique ou non des
définitions que l’on pose. Ainsi la définition selon laquelle deux vecteurs du plan
donnés par leurs coordonnées \( (u_1, u_2)\) et \( (v_1, v_2)\) dans une base sont colinéaires si
\(v_1 = v_2 = 0\)
ou s’il existe un scalaire \(\lambda\) tel que \(u_1 =\lambda u_2\) et
\(v_1 =\lambda v_2\) ne donne pas
d’algorithme pour décider si deux vecteurs ainsi donnés sont colinéaires ou non,
puisque dans chaque cas, il faut « deviner » le scalaire \(\lambda\). En revanche, la définition
alternative, selon laquelle ces vecteurs sont colinéaires si \(u_1v_2 = v_1u_2\) nous donne un
tel algorithme.
La définition : une équation diophantienne \(P(X_1, \ldots ,X_n) =0\) est
résoluble si et seulement s’il existe des entiers
\(a_1,\ldots, a_n\) tels que \(P(a_1, \ldots ,a_n )=0 \) ne
suggère pas d’algorithme pour décider si une équation diophantienne est résoluble ou
non, et on sait qu’il n’y a pas de définition équivalente qui soit algorithmique.

Une troisième étape est peut-être de montrer que la notion d’algorithme est un
formidable outil de mathématisation du réel : de mathématisation des processus de
synthèse des protéines, des processus cérébraux, des processus par lesquels nous
reconnaissons qu’une phrase est bien formée dans une langue naturelle ou dans un
langage artificiel, des protocoles ferroviaires et aériens, … et aussi, bien entendu, des
protocoles employés par les portiers dans les vaisseaux spatiaux.

Merci à Bernadette Charron-Bost qui a patiemment répondu à toutes les questions
que je lui ai posées sur l’algorithme de Peterson.

<redacteur|auteur=13>