Le mot égalité est bien connu de tous les enfants à l’école et de tout un chacun dans la société française. Il ne s’agit pas dans ces quelques pages de philosopher sur ce mot, mais simplement de s’interroger sur le sens de ce mot si commun et du signe \(=\) qui lui est associé, en mathématiques à l’école.

Que disent les programmes de l’école ?

Les programmes de 2002 de l’école maternelle excluent l’utilisation du signe \(=\) :
« La résolution des problèmes rencontrés ne nécessite pas le recours au formalisme mathématique (\(+\), \(−\), \(=\)). Celui-ci sera introduit à l’école élémentaire. »

On ne devrait donc pas voir dans les classes de maternelle d’expressions du type \(3 + 2 = 5\). De telles expressions, justes, mais proscrites par les programmes, restent assez rares. Il arrive cependant que l’on rencontre dans les écoles maternelles des écritures du type suivant :

Ces écritures, qui semblent plus anodines car moins « mathématiques », n’en sont que plus dangereuses parce que dénuées de tout sens et inductrices de conceptions erronées. Elles confondent plusieurs registres de représentations, sont clairement bannies par les programmes et doivent être interdites à tous les niveaux d’enseignement. Si certains ouvrages pour les enfants, surtout périscolaires, les utilisent, ils ne devraient pas avoir leur place dans les écoles maternelles et les enseignants ne devraient pas s’en inspirer.

Les programmes du cycle 2 précisent que « […] les élèves construisent leurs premières connaissances sur la comparaison des nombres […] », mais sont muets sur l’égalité. Ni le signe \(=\), ni les deux signes \(<\) et \(>\) n’apparaissent dans le texte du programme, ni dans sa déclinaison en compétences.

Ce n’est qu’au cycle 3 que le texte des programmes précise que « les connaissances relatives aux nombres entiers naturels concernent : […] la comparaison et le rangement de nombres […] », tout en restant muet sur l’égalité et sur le signe \(=\), comme sur les deux signes \(<\) et \(>\). Mais, dans la rubrique « ordre sur les entiers naturels », les compétences du cycle 3 indiquent que les élèves doivent savoir « utiliser les signes \(<\) et \(>\) pour exprimer le résultat de la comparaison de deux nombres ou d’un encadrement ». Les programmes ne disent toujours rien sur le signe \(=\), même si la comparaison de deux nombres peut conduire à écrire qu’ils sont égaux.

L’usage du signe \(=\) serait-il si évident, si simple que les programmes n’aient pas besoin de l’évoquer ?

Que disent les ouvrages savants ?

Le Dictionnaire des mathématiques, de A. Bouvier, M. George et F. Le Lionnais définit comme suit la notion d’égalité.

Égalité ou relation d’égalité : Relation notée \(=\) (on lit « égal »). On écrit \(a = b\) lorsque les symboles \(a\) et \(b\) représentent le même objet mathématique. En fait, l’égalité est une notion primitive des mathématiques […].

L’orthographe ou la grammaire apportent-elles une information sur le sens de ce signe ?

Écrire « égal » sans « e » ou « ent » en final le classe parmi les adjectifs. Dans une expression comme \(2 + 3\) égal, il qualifierait donc \(2 + 3\), ce qui ne correspond pas à la réalité mathématique. Il s’agit en fait du verbe égaler et l’usage permet d’écrire soit deux multiplié par quatre égale huit, soit, si l’on porte son regard davantage sur la quantité désignée, trois plus deux égalent cinq [1]

Ces interrogations grammaticales apportent un premier élément de réponse au sens même du signe =. Le Petit Robert, (1996). en écrivant « égal : qui est de même quantité, dimension, nature ou valeur », indique clairement que ce signe ne renvoie pas nécessairement à l’objet lui-même, mais à une propriété liée à l’objet, comparée à la même propriété liée à un autre objet (généralement)… Ceci est exprimé par « qui est de même »… Ainsi, écrire \(2 + 3 = 5\) ne signifie pas que les objets \(2 + 3\) et \(5\) sont les mêmes objets, mais que ces deux objets, ces deux écritures expriment une seule et même chose, désignent le même nombre. Elles sont deux écritures différentes du même nombre. L’objet mathématique dont il est question dans le Dictionnaire des mathématiques n’est donc pas nécessairement l’objet physique lui-même, mais un concept mathématique lié à cet objet.

Le signe \(=\) est un signe qui trouve sa place entre deux désignations d’un même objet, d’un même concept. Ainsi, dire \(2 + 3 = 7 − 2\) n’est pas dire que les écritures \(2 + 3\) et \(7 − 2\) sont les mêmes, mais que ce sont deux signifiants différents qui renvoient à un seul et même signifié, le nombre que l’on désigne aussi par 5 (écriture la plus compacte parmi toutes les écritures de ce nombre), de même, écrire \(AB = CD\) ne signifie pas que les objets mathématiques \([AB]\) et \([CD]\) sont les mêmes, mais que leurs longueurs sont égales.

Il est donc regrettable de voir des écritures comme :

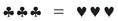
où bien évidemment aucun des deux membres ne désigne une quantité, puisque ce sont les objets eux-mêmes qui sont présents dans l’écriture et que ces objets ne sont pas les mêmes. Deux objets ne peuvent être égaux que s’ils sont identiques, par contre certaines de leurs propriétés peuvent être égales même si ces objets sont différents (masse, température, …).

Que dit l’inventeur du signe \(=\) ?

C’est en 1557 que ce signe est apparu pour la première fois dans un ouvrage édité.

Un Gallois, Robert Recorde (1510 — 1558), ne souhaitant plus écrire en toutes lettres « est égal à » a décidé, dans son ouvrage d’algèbre Whetstone of Witte [2] de remplacer cette écriture fastidieuse par le signe que nous connaissons.

 

Sa justification figure ci-contre [3].

 

En fait, l’histoire de ce signe ne nous renseigne pas sur sa définition, par contre, l’usage qui en est fait est bien l’usage actuel de ce signe.

 

Que nous disent les pratiques à l’école ?

Ce signe \(=\) est introduit très tôt dans les apprentissages c’est-à-dire dès le CP. Il vient tout naturellement lorsque l’on traite des désignations additives des nombres. Dans les pratiques et selon les auteurs de manuels, deux approches peuvent être observées.

Une première approche, la plus courante, est de considérer le signe = comme un signe initialisant un processus de calcul. Par exemple : \(2 + 3 = … \)  la réponse attendue est bien évidemment \(5\) et pas \(7 − 2\).

Une deuxième approche, bien plus rare, consiste à relier entre elles avec le signe \(=\) des étiquettes désignant le même nombre, comme le montre l’image ci-dessous.

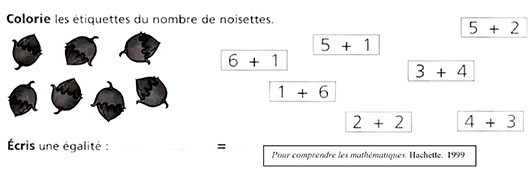
On peut regretter que cette activité de découverte du signe \(+\), donnant clairement le sens fondamental du signe \(=\) ait disparu dans l’édition de 2003.

À l’école élémentaire, le signe \(=\) s’utilise exclusivement entre deux écritures de nombres, le plus souvent comme déclencheur d’un calcul pour trouver une expression plus compacte.

Il ne faudrait cependant pas en limiter l’usage au déclenchement d’un processus de calcul et ce pour deux raisons au moins :

• La première : cet usage occulte par la pratique la propriété de symétrie de la relation d’égalité, l’amputant d’une partie de son sens.
• La deuxième : la transformation d’écritures par égalités permet bien souvent d’effectuer les calculs de manière plus simple car plus économique en mémoire. C’est la base du calcul réfléchi.

Ex 1 : Transformation par décomposition.
Celui qui connaît le résultat fondamental de \(5 + 5\) et de \(2 + 3\) peut calculer \(7 + 8\) de la manière suivante : \(7 + 8 = 5 + 2 + 5 + 3 = 10 + 2 + 3 = 10 + 5 = 15\).

Ex 2 : Exprimer autrement en ajoutant 0 sous une forme ad hoc.
\(137 − 58 = 137 − 58 + 0 = 137 − 58 + 2 − 2 = 137 + 2 − 58 − 2 = 139 − 60 = 79\).

Ce procédé permet aussi de reconnaître, sans calcul ou presque, que deux expressions sont égales comme \(137 − 58\) et \(139 − 60\).

On pourrait dire en conclusion qu’il conviendrait d’élargir les pratiques scolaires autour de l’égalité et que les programmes de l’école se devraient de prendre explicitement en compte cette notion fondamentale.

 

$$