Philippe Lombard [1].

À Henri Bareil qui m’a initié un jour, sur un coin de nappe, à la croix des mélanges…

La réflexion menée actuellement sur ce qu’il serait légitime d’envisager comme
socle pour les études primaires et secondaires remet à l’ordre du jour le problème des
objectifs à fixer à l’enseignement des mathématiques à ce niveau. À cette occasion,
je souhaiterais apporter ici quelques éléments de réflexion sur un point qui concerne
une partie non négligeable des programmes et qu’il est devenu courant de désigner
sous l’appellation : résolution de problèmes concrets.

On sait en effet que les nouveaux programmes du primaire et du collège mettent
directement l’accent sur ce type d’activités et il n’est pas difficile de voir par ailleurs
que tout l’aspect modélisation mis en avant dans l’enseignement du lycée n’est qu’un
prolongement naturel du même genre de préoccupations. Mais en posant de manière
directe la question des rapports entre mathématiques et monde réel – à tout le moins
en matière d’apprentissage –, ce sujet touche en réalité à des problématiques qui ont
toujours sous-tendu et dirigé la question des contenus de l’enseignement, même si les
choix fondamentaux n’ont pas toujours été clairement explicités. Il n’est donc peut-être
pas inutile de tenter de mettre en perspective aujourd’hui certains des aspects
importants de ce problème, et ceci au regard des évolutions quelque peu récurrentes
des différents points de vue sur le sujet…

Je vais essayer d’analyser la question sous un éclairage à la fois très précis et très
général : que peut-on envisager comme niveau de culture à donner à l’enseignement
de l’école primaire en matière de résolution de problèmes, quel niveau de culture
faut-il se fixer comme but pour les années de collège ? On a souvent résumé la
différence entre ces deux niveaux en termes de rupture séparant résolution
arithmétique et résolution algébrique des problèmes. Notre but sera donc
précisément de s’interroger sur cette rupture (si tant est qu’elle existe encore), sur les
liens, les transitions, les liaisons – comme on dit désormais – entre ces deux niveaux
d’enseignement…

1. Le problème de la laitière

Intéressons-nous pour commencer à un problème extrait d’un manuel (Châtelet
1934) destiné au niveau « Cours Moyen et Fin d’études » :

« Une laitière a fourni à une crémière 20 litres de lait. En pesant ce lait, la crémière a trouvé un poids de 20,555 kg. Ce lait a-t-il été mélangé d’eau ? Qu’est-ce qui le prouve ? Quelle quantité d’eau contient-il ? On rappelle que la densité du lait est 1,03 »

Je ne dois pas me tromper énormément si j’affirme que très peu d’élèves
d’aujourd’hui sauraient faire aisément cet exercice, ou même que relativement peu
de professeurs (d’école ou de collège … voire de lycée) sont enclins à trouver qu’il
est facile. L’explication de ce phénomène est, évidemment, plus à trouver dans le
contenu moderne ou post-moderne de l’enseignement des mathématiques depuis
trente-cinq ans que dans la disparition de la coutume qui consistait à aller chercher
son lait à la ferme ou chez la crémière avec son pot au lait… Et on peut d’ailleurs
constater que le plus grand nombre des personnes qui parviennent à résoudre le
problème le font « par l’algèbre »… et peinent énormément – faute de l’avoir appris
un jour – à dégager une solution de type « arithmétique », c’est-à-dire « par le
raisonnement ».

Cela pose évidemment en pleine lumière la question de ce qu’il est convenu
d’appeler les savoirs pérennes. Certains considèrent, presque sans discussion
possible, que ce qui était naguère enseigné à l’école primaire devrait constituer un
bagage inaliénable, d’autres partent du principe que les compétences requises
aujourd’hui doivent être choisies en fonction des quelques dogmes régissant une
« transposition didactique » bien sentie. Il est cependant indiscutable que c’est une
question non triviale de savoir si les problèmes du type de celui de la laitière font
partie des apprentissages pérennes ou, à tout le moins, de savoir dans quelle mesure
les méthodes de résolution par l’arithmétique sont ou non des savoir-faire
indispensables aux élèves d’aujourd’hui.

Bref. On en revient toujours aux mêmes difficultés : « Quel type de problèmes
faut-il enseigner en primaire ? », « Quel type d’outils de résolution faut-il
apporter ? »… Considérons donc, pour commencer, le problème de la laitière comme
un problème primaire et essayons de voir ce que cette idée peut recouvrir. Ce qui est
manifeste tout d’abord c’est que le côté « concret » de l’énoncé est certainement
secondaire en matière d’instruction : ce qui importe avant tout c’est le côté
« métaphorique » de l’exercice et c’est surtout le côté « analogique » de
l’apprentissage. L’élève ne saura faire le problème de la laitière que s’il a appris à
résoudre un certain corpus de problèmes semblables, que s’il est capable de trouver
dans sa mémoire le problème-type auquel ramener celui qu’on lui pose, et que s’il
sait effectuer les permutations correctes pour passer de son problème de référence à
celui qu’il vient de rencontrer. Qui donc pourrait prétendre inventer la solution au
problème de la laitière s’il n’a pas d’abord un « métier » suffisant dans la résolution
de problèmes relativement proches ?

1°) Solutions arithmétiques

Quelle était donc la solution demandée en 1934 ? Je ne la connais pas dans tous
ses détails rituels, mais il semble bien que l’élève devait savoir répondre à deux
variantes d’une même question :

1. savoir déterminer la « densité » du produit acheté,
2. savoir trouver, connaissant explicitement ou non cette densité, les proportions
   exactes de « l’alliage » d’eau et de lait qui a été fourni par la laitière.

On notera d’ailleurs pour commencer deux choses qui montrent bien que l’élève
doit avoir acquis un métier non négligeable pour réussir l’exercice. C’est très visible
pour tous ceux qui, justement, non pas acquis ce métier. D’une part, le sens du mot
« lait » dans l’énoncé ne peut être bien maîtrisé par un élève de ce niveau que s’il a
pris l’habitude de se retraduire ce genre de texte sous forme « opérationnelle ».
Sinon, il risque fort de ne pas distinguer de quel « lait » il s’agit (le vendu ou le pur)
dans chacune des quatre occurrences où ce mot apparaît dans le texte. D’autre part,
on remarquera que l’indication donnée (« On rappelle que la densité du lait est
1,03 ») est tout à fait typique – et de toute éternité ! – des exercices de
mathématiques : d’abord elle donne une information indispensable (le nombre 1,03),
ensuite elle souffle que le problème est un problème faisant appel aux densités, enfin
elle demande cependant à l’élève de savoir précisément ce que veut dire le mot
densité…

Cela étant, la réponse à la question 1) est normalement assez facile car il s’agit de
trouver le poids d’un litre du liquide acheté : 20,555 divisé par 20 égale 1,027 75.
Une fois levée la petite difficulté de langage entre densité et poids d’un litre, on peut
dire qu’il n’y a ici que la difficulté (non négligeable) de réussir la division et la
difficulté arithmétique de travailler avec des nombres qui sont finalement très
compliqués. Mais une première conclusion découle de ce résultat : le lait n’est pas
pur… Il reste alors la question 2) : sachant que la densité du mélange est de 1,027 75,
quelle est la quantité d’eau contenue dans ce liquide ?…

Poursuivons donc. Nous sommes désormais devant un problème difficile, aussi
bien pour les élèves que pour la plupart des maîtres, toutes époques confondues… Et,
si l’on admet que la première question est parfaitement élémentaire au niveau de la
compréhension, disons du « sens de la division », c’est à propos de cette deuxième
question que je voudrais essayer d’analyser les réponses possibles et les savoirs, ou
savoir-faire, qu’elles mettent en jeu. (J’espère aussi montrer au passage que
l’ingéniosité de l’esprit humain est époustouflante, mais je n’y insisterai pas
systématiquement.)

a) La croix des mélanges. Cette méthode ne demande pas de comprendre – mais
qu’est-ce que « comprendre » ? –, elle repose sur deux recettes éprouvées et elle
pourrait bien mettre en jeu au passage (et par deux fois, s’il vous plaît) le symbolisme
de la croix… Voici la réponse, qui nécessite deux temps :

Premier pas : le problème me demande de mélanger un liquide de densité 1 avec un
liquide de densité 1,03 de manière à trouver un liquide de densité 1,027 75, je sais
alors qu’il me suffit d’écrire et de compléter la « croix des mélanges » suivante :

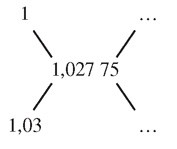
Pour cela je mets en haut 1,03 − 1,027 75 = 0,002 25 et en bas 1,027 75 − 1 =
0,027 75, j’obtiens :

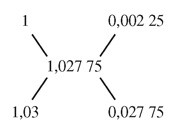
Je peux donc dire : « pour obtenir un mélange de la densité 1,027 75 cherchée, il
suffit de mélanger 0,002 25 unités du liquide de densité 1 (l’eau) et 0,027 75 unités
du liquide de densité 1,03 (le lait pur). Autrement dit, je dois mélanger 225 parts avec
2 775 parts et, si je simplifie par 75, je vois finalement qu’il faut un mélange qui
corresponde à 3 parties d’eau pour 37 parties de lait…

Deuxième pas : cela me donne 3 litres d’eau pour obtenir 37 + 3 = 40 litres de
mélange, il y aurait ensuite (si le problème était plus compliqué…) une question de
proportionnalité pour trouver la quantité correspondante dans le cas de la laitière.
Nous aurions alors besoin de faire appel à une deuxième croix (dite « du produit en
croix ») pour terminer le raisonnement. Mais ici, il est immédiat que les 20 litres
correspondent à la moitié du résultat obtenu : je peux donc conclure qu’il y a 1,5
litre(s) d’eau dans le mélange.

J’imagine que chacun de ceux qui ont pris la peine de lire le paragraphe précédent
sont un peu interpellés (comme on dit aujourd’hui) par le côté magique de la solution
reposant sur la croix des mélanges. J’espère même un peu, pour tout dire, que ceux
qui savaient résoudre le problème « par l’arithmétique » (c’est-à-dire « par le
raisonnement ») trouvent qu’il y a une forme de tricherie dans la solution exposée…
En voici une autre qui relève un peu de la même magie et qui reposerait aussi sur une
présentation en croix, comme cela a été le cas au moins jusqu’au 17ème siècle.

b) La méthode de fausse(s) position(s). Considérons le poids de 20 litres d’un
liquide composé d’eau (pesant 1 kg le litre) et de lait (pesant 1,030 kg le litre).
Envisageons (par exemple) deux cas extrêmes :
 Si le mélange contient 0 litres de lait, il pèse 20 × 1 kg = 20 kg, puisqu’il n’y a que
de l’eau,
 Si le mélange contient 20 litres de lait, il pèse 20 × 1,030 kg = 20,600 kg, puisqu’il
n’y a que du lait.
Cela fait donc 0,600 kg = 600 g de plus. Si bien que l’on peut énoncer : un
accroissement du volume de lait de 20 (litres) entraîne un accroissement du poids du mélange de 600 (grammes).

Or la crémière n’a observé qu’un accroissement du poids du mélange de 555
(grammes) ! Cela prouve évidemment que ce mélange est de mauvais aloi, mais il
reste à dire : 20 (litres) de plus ont entraîné une augmentation de 600 (grammes),
donc pour obtenir une augmentation de 555, il faut en fait 20 × (555 / 600) litres de
lait. Soit 18,5 litres de lait dans le mélange… Ce qui correspond bien à la présence
de 1,5 litre(s) d’eau.

Enfin voici la méthode « raisonnée » la plus classique :

c) Les fausses suppositions. C’est sans doute la méthode à laquelle on pense le
plus souvent lorsque l’on évoque la solution arithmétique. Elle revient à un savoir-faire
très parent du précédent, tout aussi oublié d’ailleurs, mais qui consiste à ne plus
raccrocher analogiquement notre énoncé initial à des problèmes d’alliages mais
plutôt à des problèmes un peu plus généraux, que l’on pourrait très légitimement
qualifier aussi de problèmes de mélanges, mais que la tradition rapporte aux
problèmes dits « de fausses suppositions ».

Un exemple type aujourd’hui (ou paradigmatique, si l’on préfère) est le suivant :
« J’ai 215 euros dans ma tirelire. Cette somme est constituée de billets de 5 et de 10
euros. Il y a 30 billets en tout. Combien ai-je de billets de chaque sorte ? ». La
solution raisonnée peut alors être présentée sous la forme : « Si je n’avais que des
billets de 5, ma tirelire contiendrait 30 × 5 = 150 euros, mais j’ai 215 euros, donc 65
euros de plus. Or chaque fois que je remplace un billet de 5 par un billet de 10, je
mets 5 euros de plus dans la tirelire… Donc il faut que je change 65 / 5 = 13 billets
de 5 en billets de 10. Résultat : 13 billets de 10 et 17 billets de 5… ».

Reprenons alors le problème de la laitière : « si les 20 litres étaient du lait, le
mélange pèserait 20,600 kg, mais il pèse 20,555 kg, donc 45 g de moins. Or chaque
fois que l’on remplace un litre de lait par un litre d’eau, on enlève 0,030 kg = 30 g
au poids total… Donc il faut changer 45 / 30 = 1,5 litre(s) de lait en litre(s) d’eau.
Résultat : il y a 1,5 litre(s) d’eau et 18,5 litres de lait… »

2°) Solutions algébriques

Après ces quelques réponses que l’on peut rassembler sous le terme de
« résolutions de niveau primaire », intéressons-nous aux deux ou trois principales
solutions de type « collège » tout en essayant de comprendre les « ruptures » que cela
suppose par rapport au point de vue précédent. Le cadre général de ce changement
est naturellement celui du passage à « l’algèbre », toutefois je dirai plutôt un passage
au « calcul avec des lettres », car il y a plusieurs manières de prendre du recul par
rapport au problème de la laitière. Mais commençons par noter que, jusqu’ici,
l’énoncé du problème est relativement connoté « résolution par le raisonnement »
dans la façon même dont il est rédigé. Même si sa formulation n’est pas sous une
forme « moderne » telle que :

« Une laitière a fourni à une crémière 20 litres de lait. En pesant ce lait, la
crémière a trouvé un poids de 20,555 kg.
1/ Ce lait a-t-il été mélangé à un autre liquide ? Qu’est-ce qui le prouve ?
2/ Supposons que cela soit de l’eau. Quelle quantité d’eau contient-il ?
On rappelle que la densité du lait est 1,03. »

Il n’en reste pas moins qu’il suggère nettement un ordre dans la démarche : il
oblige à répondre vraiment à la question sur la pureté avant d’entamer le calcul qui
permet de déterminer précisément la quantité d’eau présente dans le mélange. Or,
comme nous allons le voir, les solutions de niveau collège cherchent en fait à
répondre directement à la question quantitative, avant même de répondre à la
question de la pureté du lait acheté. Ce n’est en fait que si le résultat final est « il y a
0 litre d’eau » que l’on conclura que le lait acheté n’est pas mouillé…

La mise en équation du problème suppose donc un changement de démarche à ce
niveau, mais ce n’est pas là l’essentiel. La vraie « rupture » avec les approches
précédentes est à comprendre sous deux aspects. Classiquement, les problèmes
résolus par des méthodes arithmétiques sont de deux types :

 les problèmes élémentaires qui se résolvent en « renversant les opérations ». Par
exemple : J’ai deux billets de même valeur et une pièce de 2 euros, combien vaut
chaque billet sachant que j’ai 102 euros en tout ? Il suffit de « remonter le calcul qui
conduirait à obtenir le total : j’enlève 2 à 102 et il me reste le prix des 2 billets, puis
je divise par 2 ce montant pour obtenir la valeur d’un billet…

 les problèmes non élémentaires pour lesquels le renversement de la succession
d’opérations ne marche pas directement. Par exemple : J’ai un nombre, je le multiplie
par 3 et j’ajoute 5, trouver ce nombre sachant que le résultat de l’opération
précédente est le même que si je prends le nombre, que je le multiplie par 15 et que
j’enlève 21. Il faut ici quelques contorsions pour obtenir le résultat en se contentant
de chercher un chemin parmi les opérations à faire. C’est précisément le cas du
problème de la laitière.

La supériorité de la méthode algébrique est qu’elle permet de traiter ces
problèmes sans vraiment se contorsionner pour découvrir le chemin qui « remonte »
au résultat et qu’elle s’applique à des tas d’autres énoncés pour lesquels on serait bien
en peine de trouver la solution autrement. On pourrait noter au passage qu’il n’y a
pratiquement aucun problème de niveau collège qui rendrait absolument
indispensable l’introduction de cette méthode de résolution « par l’algèbre »… Mais
revenons plutôt à notre laitière. La démarche consiste à mener la lecture de l’énoncé
en effectuant les calculs aussi bien avec les données connues qu’avec les données
inconnues. L’élève doit donc apprendre à dire : « Les 20 litres de mélange sont
composés d’une certaine quantité x [litres] d’eau et donc d’une quantité (20 − x)
[litres] de lait pur. Dès lors le poids total s’obtient en calculant directement, mais en
gardant le nombre mystérieux x de litres sous la forme de « lettre » :

x × 1 + (20 − x) × 1,03 = 20 × 1,03 − 0,03 × x = 20,6 − 0,03 x

Or l’énoncé nous apprend que la quantité que l’on vient d’obtenir est égale à
20,555 [kg]. Il reste alors à résoudre l’équation : 20,6 − 0,03 x = 20,555 et (par
prudence…) à vérifier que la valeur obtenue marche effectivement. »

Avant de voir quelques variantes à cette solution algébrique, nous pouvons nous
arrêter sur quelques remarques importantes en ce qui concerne le point qui nous
occupe, c’est-à-dire celui de la « rupture » entre deux « niveaux de culture ». J’ai dit
plus haut que la hiérarchie des questions était modifiée et que l’élève devait l’avoir
compris au préalable pour réussir, mais il clair que, une fois rentré dans ce nouveau
jeu, la solution devient accessible à un plus grand nombre d’élèves. Elle ne demande
« que » de savoir lire l’énoncé en conduisant les calculs avec des lettres et, ensuite,
« que » de savoir résoudre l’équation… Mais, là encore, on aura sans doute noté au
passage que cette conduite des calculs n’est plus tout à fait la même que celle de la
démarche du primaire. En effet, il faut bien voir que désormais, d’une part les unités
se doivent d’être proscrites lorsque l’on arrive à l’équation et que, d’autre part,
l’ordre des opérations peut changer un peu de « sens » par rapport à leur
apprentissage originel… Je veux dire par là que si l’élève a appris à écrire que le
poids de x litres est x fois le poids d’un litre, il écrira d’abord le résultat sous la forme
x × 1,03 et il sera ensuite obligé de prendre l’habitude de l’écrire sous la forme
1,03 × x pour obtenir 1,03 x.

Tout cela signifie que nous sommes désormais dans l’univers des calculs
algébriques. D’abord il impose des contraintes du type précédent, ensuite il va
fournir des solutions qui seront découvertes simplement au niveau du calcul
« mécanique », enfin il lui arrivera même d’apporter des « solutions surprises » qui
résultent de la logique propre de cet univers de l’algèbre et pas forcément de la
logique de l’énoncé « concret » d’origine. Pensez par exemple au cas où on trouve,
en plus des valeurs cherchées, des solutions négatives qui n’ont jamais eu grand -chose
à voir avec les crémières ou les laitières ! C’est là un point de « rupture –
chevauchement » invisible au niveau du collège mais qui doit s’opérer
progressivement pour aboutir à une acceptation franche de cet univers algébrique au
niveau du lycée. Pour le dire un peu différemment : dans la solution algébrique
précédente la lettre x représente un « nombre masqué », mais c’est en quelque sorte
un vrai nombre avec lequel on travaille au moment de la « mise en équation », sans
le connaître, mais comme avec un nombre habituel. Or au niveau mathématique,
dans le cours de la démarche, ce nombre masqué n’est plus vraiment un nombre, il
devient subrepticement ce que l’on appelle savamment une « indéterminée » (pour
ne pas dire tout simplement une « lettre ») qui prend au final un statut différent des
nombres eux-mêmes. (Mais c’est une autre histoire…)

Comme chacun le sait, je n’ai indiqué précédemment que la mise en équation la
plus simple, dans la mesure où elle consiste à choisir une seule quantité inconnue.

Voici au moins deux variantes importantes :

a) Système à deux inconnues. Une première variante intéressante consiste à
choisir deux inconnues, en appelant par exemple x le nombre de litres d’eau et y le
nombre de litres de lait. C’est un peu plus savant et cela aboutit en fait à un « système
d’équations » car il faut cette fois traduire algébriquement deux conditions :
 le nombre de litres total est égal à 20 : x + y = 20 ;
 le poids du mélange est égal à 20,555 : x × 1 + y × 1,03 = x + 1,03y = 20,555.

Les manières de résoudre ce système peuvent alors constituer des variantes plus
ou moins importantes et instructives :

 si je « tire y en fonction de x » dans la première équation pour le reporter dans la
deuxième, je retombe exactement sur l’unique équation en x que j’ai résolue au point
précédent,
 si je multiplie la première équation par 1,03 et que j’enlève la deuxième à
l’équation obtenue (ou si je soustrais simplement la deuxième à la première telle
quelle), j’obtiens un calcul qui correspond (une fois traduit) à la méthode des fausses
suppositions,
 si je traduis directement ce système en termes d’équations de droites, je peux
obtenir une interprétation et une lecture géométriques de la résolution…

b) Calcul littéral absolu. Une seconde variante, encore plus savante, consiste à
résoudre une bonne fois pour toutes l’infinité des problèmes d’alliages, de mélanges,
de crémières, de laitières ou de pots au lait, etc., en cherchant la solution d’un
problème « générique » où les autres données elles-mêmes sont écrites sous forme
de lettres. Ainsi Newton aurait posé, avant de résoudre le problème de la laitière :
« Une laitière a fourni à une crémière V litres de mélange d’un liquide de densité d
et d’un liquide de densité d ’. En pesant ce mélange, la crémière a trouvé un poids de
P kg. Quelle quantité de chaque liquide ce mélange contient-il ? ». Puis il aurait posé
l’équation précédente dans toute sa généralité : Soit x le volume du premier liquide,
le poids total P du mélange est donné par la relation : P = d x + d ’ (V − x) . D’où l’on
tire x = (P − d’ V) / (d − d ’)… Il suffirait alors de remplacer les lettres par les données
convenables pour chaque problème de type « mélange », etc.

Je laisse (à titre d’exercice) le lecteur retraduire le problème sous la forme : « Une
laitière a fourni à une crémière V litres de mélange d’un liquide de densité d et d’un
liquide de densité d’. En pesant ce mélange, la crémière a trouvé une densité d "
Quelle quantité de chaque liquide ce mélange contient-il ? ». Il suffira de le résoudre
tel quel pour s’apercevoir que la solution obtenue peut ensuite se mettre sous la
forme : « les nombres cherchés sont proportionnels aux deux nombres obtenus par
l’algorithme qui est condensé dans ce qui a été appelé plus haut la croix des
mélanges ».

3°) Le point de vue fonctionnel.

Il n’est pas possible de s’arrêter aux deux types de regards précédents
(arithmétique et algébrique) car le « niveau de culture » collège introduit aussi (de
manière plus ou moins soutenue) un troisième regard sur les problèmes que nous
cherchons à résoudre ici. Il s’agit de glisser à une interprétation des objets manipulés
(nombres, quantités, équations, …) qui consiste à les éclairer sous l’angle de la
notion de « fonction ». Cela va nous faire passer par une nouvelle « rupture » entre
notion d’inconnue et notion de variable.

Revenons en effet à la mise en équation qui nous a conduits à exprimer le poids
total (20,555) à partir des données connues, auxquelles nous avons appris à mêler le
nombre inconnu que nous avions appelé x. Nous avons obtenu la formule :
20,6 − 0,03x = 20,555 . Comme je l’ai dit à ce moment-là, x désignait dans tout ce
calcul un nombre bien précis : celui que l’on cherche. Cependant – par une nouvelle
rupture qui nous oblige une nouvelle fois à changer de point de vue ! – nous pouvons
maintenant regarder différemment cette formule en disant : le membre de gauche
représente ce que l’on trouve comme poids à partir de la valeur de x que nous ne
connaissions pas. Nous avons écrit que cela était égal à la valeur 20,555, mais nous
pouvons introduire cette manière de regarder « de plus loin » le membre de gauche
en parachutant une nouvelle lettre, par exemple P, pour dire quelque chose de très
différent : « si nous donnons au volume d’eau une valeur x quelconque, nous
trouverons toujours que le poids final P est égal à la quantité 20,6 -0,03x. »

Puis nous dirons : « Le problème actuel de la crémière est qu’elle a reçu un
mélange pour lequel P s’avère être égal à 20,555, pouvons-nous déterminer, parmi
toutes les valeurs possibles de x la valeur qui conduit à trouver précisément cette
valeur P = 20,555 ? ». Toute la question tient désormais dans des considérations sur
cette « fonction » que nous avions trouvée au cours de l’algébrisation :
P = 20,6 − 0,03x ou, si l’on préfère, sur la fonction classiquement notée
y = 20,6 − 0,03x. La seule différence est que, si nous avions cherché à trouver cette
« fonction » au lieu de l’équation, nous n’aurions pas mené les calculs en pensant que
la lettre représentait la valeur précise cherchée dans le problème, mais qu’elle portait
en elle, en quelque sorte, toutes les valeurs possibles. C’est une nouvelle « rupture –
chevauchement » pour l’élève, mais elle concerne plus (du moins il me semble) la
transition collège – lycée, bien que la période des maths modernes ait très fortement
modifié ce genre de problématique pendant quelques années…

Notons simplement ici, pour boucler notre promenade dans les méthodes de
résolution, que la méthode dite de(s) fausse(s) position(s) n’est rien d’autre qu’une
conséquence de ce que je viens de dire : le poids du mélange étant une fonction
affine, il nous suffisait effectivement de déterminer deux valeurs particulières du
résultat en se donnant deux valeurs arbitraires de la variable pour pouvoir déterminer
(par proportionnalité) la valeur qui donne le bon résultat… Le lecteur un peu
philosophe notera aussi au passage que nous sommes peut-être en face de la méthode
de résolution qu’il nous faut considérer, en définitive, comme la plus concrète, la plus
savante et … la plus pérenne ! Que fait en effet un scientifique devant un problème
quelconque ? Oh ! comme on dit (aussi) aujourd’hui, il « modélise », bien sûr ! Mais
il espère surtout deux choses : d’abord que le phénomène qu’il étudie sera finalement
décrit par une certaine fonction des paramètres dont il dispose, et ensuite que cette
fonction ne sera pas suffisamment « explosive », pour pouvoir l’approcher
raisonnablement par une fonction affine dans la zone raisonnable où il fait appel à
elle… Dès lors le premier réflexe d’un physicien ne serait sans doute ici rien d’autre
que la méthode des fausses positions suivie, comme nous l’avons fait, d’une
interpolation linéaire à partir des valeurs choisies comme valeurs-témoins. La
crémière du problème n’a pas fait autre chose ! Et elle a eu (en prime) la chance que
son approximation affine soit précisément la fonction exacte… Et, qui sait, elle aurait
peut-être même pu le savoir à l’avance en invoquant correctement les bons
arguments d’invariance, de symétrie ou d’optimisation si chers aux grands
scientifiques de notre époque ?

4°) La rupture primaire - collège

Mais nous venons de faire le tour d’un certain nombre d’approches possibles pour
le problème de la laitière et je pense avoir donné et détaillé l’éventail des solutions
praticables par l’école et par le collège. Cependant, j’ai implicitement (et
volontairement) choisi ce que j’ai considéré comme une approche « culture
primaire » (sans calcul littéral) et comme une approche « culture collège » (avec
calcul littéral). Ceci est évidemment un choix qui doit être justifié. Je vais essayer de
m’expliquer et de préciser ce que j’ai voulu dire en parlant au passage de « rupture
– chevauchement » ou même de « palimpseste ».

On pouvait naturellement considérer que, depuis un certain temps, la progression
« arithmétique puis algèbre » avait fait ses preuves et qu’il n’y avait pas lieu de
changer cet état de fait. C’est oublier, d’une part, que le problème de savoir s’il fallait
enseigner les méthodes littérales plutôt que les méthodes arithmétiques a été posé de
bonne foi à toutes les époques et que, d’autre part, on a effectivement tenté un jour
l’expérience qui consistait à tout chambouler : ce fut la période des maths modernes.
Il me paraît important de comprendre le renversement constitué par les maths
modernes en s’arrêtant non seulement sur quelques points cruciaux du changement
qui avait été opéré par les programmes de 70, mais aussi sur certains aspects
fondamentaux du retour en arrière effectué lors de la contre-réforme de 1985. Sans
chercher à être exhaustif, on peut mettre l’accent sur au moins deux aspects
fondamentaux, l’un concerne la résolution de problèmes et l’autre l’introduction des
outils algébriques.

Le changement de rapport à la résolution des problèmes dits concrets (du type de
celui de la laitière) marqué par la réforme des maths modernes est particulièrement
frappant. Le choix épistémologique opéré à l’époque consistait avant tout à
considérer que les nombres devaient s’apprendre d’abord en tant « qu’objets
mathématiques abstraits » pour pouvoir seulement ensuite être investis dans des
situations où il s’agissait de résoudre des problèmes. D’une certaine manière, cet
apprentissage des nombres et des opérations s’est mis à fixer un objectif qui devenait
étranger à toute résolution de problèmes et les élèves apprenaient du cours sans
pratiquement aucune activité de recherche sur des énoncés plus ou moins difficiles.

La contre-réforme de 1985 a remis à l’ordre du jour la résolution de problèmes
dits concrets dans l’enseignement des maths. Cela a correspondu à la mise en avant
des « activités » préparant les chapitres de cours, ainsi que les démarches du type
« problèmes ouverts ». Mais parallèlement, par compensation pourrait-on dire, l’idée
que la résolution d’un problème non mathématique relevait de la « modélisation » a
été véritablement explicitée à ce moment-là et continue à imprégner fortement la
conception actuelle de tous les programmes. C’est une idée différente de celle qui
avait cours avant les années 70 : c’est le point de vue selon lequel la résolution d’un
problème consiste à chercher dans la panoplie des outils mathématiques ceux qui peuvent s’appliquer à la situation donnée, sachant que ces outils sont toujours
« appris pour eux-mêmes » dans un contexte qui doit rester mathématique, c’est-à- dire
largement abstrait.

Je ne suis évidemment pas certain d’avoir raison, mais ma position personnelle
est que la construction du savoir et des capacités mathématiques repose sur la
domestication de situations plus ou moins « concrètes », ou à tout le moins
« métaphoriques ». Le lecteur de ce texte doit donc prendre éventuellement en
compte ce genre de présupposé s’il désire adopter un recul critique par rapport à mon
analyse. Pour le dire un peu autrement, je pense que la stratégie « constructiviste »
prônée au moment des maths modernes n’a jamais surmonté le paradoxe suivant
entre abstrait et concret : s’il s’agit d’introduire des notions abstraites comme les
objets ou les méthodes mathématiques, on ne peut demander à un enfant de participer
à la construction de son savoir que si, précisément, on lui offre l’occasion
« d’abstraire »… Et on voit mal en quoi peut consister l’action « d’abstraire », si on
ne dispose pas, à la base, d’un corpus d’exemples familiers à partir desquels il y a
quelque chose à abstraire…

Parallèlement, la période des maths modernes a profondément bouleversé le
rapport au calcul littéral. La volonté d’introduire les concepts algébriques (les
nombres et les opérations) avant toute intervention de ceux-ci dans des situations-problèmes
autres que celles qui touchent à des considérations simples de la théorie
des ensembles et à des problématiques purement internes à l’algèbre elle-même, a
conduit le discours à utiliser d’emblée le langage et les notations de l’algèbre elle-même.
Par exemple : comment pouvait-on alors introduire la notion de division
autrement qu’en disant quelque chose comme « le quotient d’un nombre a par un
nombre b est le nombre x tel que bx = a » ? Ce qui revenait d’ailleurs à l’époque à
présenter très tôt les choses sous la forme : « ce nombre x n’existe pas forcément et
nous allons inventer des nombres qui permettent de répondre à la question »… On
voit là – entre autres… – une introduction du symbolisme faisant appel aux lettres
sous un angle encore bien plus abstrait que ce que j’ai essayé de décortiquer
précédemment en distinguant l’usage de la lettre « inconnue », de la lettre
« indéterminée » et de la lettre « variable », à propos d’une résolution de problème !

C’est principalement sur ce dernier point que je considère qu’il vaut sans doute
mieux partir de ce que j’ai appelé le niveau de culture primaire, qui ne fait pas appel
aux lettres dans les calculs, pour passer seulement ensuite à l’utilisation des lettres
dans l’initiation à un niveau de culture secondaire. Il me semble en effet que l’école
peut très bien se contenter de n’utiliser les lettres que pour la mémorisation de
formules comme celles qui donnent le périmètre ou l’aire d’un rectangle ou,
évidemment, de figures plus complexes. Et cette pratique me semble, à l’inverse,
indispensable, de même qu’il peut être important d’avoir rencontré la lettre « pi »
pour désigner le nombre en question. Mais en tout état de cause, je penche
personnellement pour un usage de lettres ayant une signification précise à ce niveau
(L, p, S, V,\(\pi\) , etc.) et pour une introduction des lettres comme x, y, … ou même a,
b, … uniquement au collège.

En résumant, je dirai donc que toutes les analyses précédentes sont implicitement
sous-tendues par deux idées :

a) que les mathématiques se découvrent progressivement en apprenant à résoudre des
problèmes ; qu’il s’agisse de problèmes habillés par des éléments de la vie
quotidienne, qu’il s’agisse de problèmes de sciences physiques (au sens large), ou
qu’il s’agisse de problèmes de géométrie élémentaire (dont on me permettra
d’ailleurs de penser qu’ils font partie des problèmes précédents) ;

b) que ce sont précisément ces résolutions de problèmes menées progressivement
d’un niveau « arithmétique » à un niveau « algébrique » qui permettent de
s’approprier petit à petit le langage, les outils et le formalisme mathématiques.

Mais il faut avoir conscience que nous sommes ici devant un problème
pédagogique difficile et aussi devant une problématique épistémologique
particulièrement profonde. La question sous-jacente peut être exposée en termes de
« savoirs pérennes », mais ce n’est jamais qu’une façon équivalente de présenter le
problème ! Car il n’y a pas que l’évolution historique qui doit nous guider.
Prenons
l’exemple de la notion de « nombre réel » qui est aujourd’hui cachée (et de manière
extraordinairement performante) dans l’usage de l’écriture décimale. Elle nous
économise un chemin énorme dans l’apprentissage du concept de nombre. Bien des
considérations métaphysiques « à la grecque » autour de ce concept peuvent et
doivent être aujourd’hui mises de côté dans l’enseignement. Les « maths modernes »
ont cru un peu imprudemment que le temps était venu de parier qu’un phénomène
analogue pouvait se produire si l’on décidait de présenter les mathématiques à partir
de la notion d’ensembles… Ce fut un péché contre la dialectique immanente qui doit
conduire les réflexions sur l’enseignement ! Prenons garde de ne pas commettre le
même genre de péché en fonçant tête baissée dans des solutions miracles…

2. — Une rupture palimpseste ?…

Avant d’en arriver à des considérations un peu plus précises au niveau
pédagogique, je m’arrêterai un moment sur un problème proposé (semble-t-il) aux
écoliers de Singapour et qui va me servir d’exemple introductif pour ce qui va
suivre :

« Un homme a deux terrains, le premier deux fois plus grand que l’autre, sur
lesquels il cultive des haricots verts. Venu le temps de la récolte, il engage une équipe
de paysans pour la faire. Toute l’équipe travaille d’abord au grand terrain pendant
cinq heures d’une matinée, et après leur pause de midi, une moitié d’entre eux va
s’occuper du petit terrain, tandis que les autres retournent au grand. Après cinq
heures de travail, ils rentrent chez eux. Un des terrains est achevé, mais pas l’autre.
Un des paysans se porte volontaire pour le finir le lendemain. Il y arrive juste en
travaillant toutes les dix heures du jour de travail. Question : Combien y avait-il de
paysans ? »

Essayons d’analyser le problème, en tentant certes de le résoudre, mais en gardant
à l’esprit que notre but n’est pas uniquement de trouver le résultat ; c’est aussi d’en
tirer des leçons sur l’apprentissage…

La première remarque qui saute aux yeux est qu’il s’agit d’un problème difficile,
que ce soit pour l’élève ou pour le maître. Pourquoi ? D’abord l’énoncé est long et
compliqué. Ensuite il contient des données qui semblent relever essentiellement de
la durée, alors que l’on s’interroge sur un nombre de paysans. Enfin on ne peut pas
dire qu’il ressemble à un « type » de problème classique (du moins pour nous) et que
l’on puisse donc procéder aisément par analogie, à la manière dont on pouvait
résoudre le problème de la laitière à l’époque où il avait été posé. Et, comme si cela
ne suffisait pas, les auteurs ont même pris un malin plaisir à ne pas indiquer lequel
des deux terrains est terminé en premier ! Tous ces éléments font évidemment que
nous ne sommes absolument pas en face d’un problème qui pourrait être donné au
CM (ni actuellement, ni naguère, ni jadis…) et encore moins dans les anciennes
classes de fin d’études primaires. En tout cas, je ne vois pas sur quels arguments a
priori je pourrais me fonder pour analyser la question à la manière du problème de la
laitière, en disant : « c’est un problème de tel type et je vais vous raconter… ».

Nous avons cependant acquis précédemment un métier et nous allons essayer de
faire fructifier notre culture secondaire… La première difficulté est d’apprivoiser
suffisamment les données pour se rendre compte que le fond du problème réside dans
le fait que les surfaces correspondent en définitive aux heures de travail et que la
seule grandeur à manipuler est de ce type-là. Encore convient-il de choisir une unité
pour utiliser correctement les informations, nous pourrions parler en « heure de
travail », je retiendrai plutôt la « demi-journée de travail » (pour un paysan) parce
que cela va simplifier un peu les nombres. Relisons alors l’énoncé en l’éclairant sous
cet angle et en préparant une « mise en équation »…

« Un homme a deux terrains A et B. Le premier nécessite deux fois plus de temps
de travail que le deuxième. Pour la récolte, une équipe de 2N paysans travaille une
demi-journée sur A, puis une équipe de N paysans travaille une demi-journée sur A
et une équipe de N paysans travaille une demi-journée sur B. Il reste alors à travailler
deux demi-journées pour terminer le champ qui n’a pas été achevé ».

L’énoncé est ainsi « restructuré » pour être plus utilisable en tant que « problème
mathématique ». On notera au passage qu’appeler l’effectif cherché 2N (au lieu de
X) n’est pas vraiment indispensable ; c’est simplement une question de métier car
cela évite d’avoir à écrire des X/2… Mais, arrivés à ce point, nous devons décider
lequel des deux champs est terminé en premier. Nous choisirons A, en attendant de
pouvoir trouver un truc pour décider vraiment. Il faudra simplement nous souvenir
qu’il est peut-être nécessaire d’envisager que ce soit en réalité le terrain B.
Écrivons
alors ce que nous savons des quantités de travail (en demi-journées) pour chacun des
deux terrains :
 Pour le champ A, il faut 2N + N = 3N demi-journées de travail,
 Pour le champ B, il faut N + 2 demi-journées de travail.
Donc, puisque nous savons que le champ A nécessite deux fois le travail du champ
B, nous avons aisément l’équation qui va gouverner le problème : 3N = 2 (N + 2) .

Je ne pense pas que cette équation soit très complexe. Il vient immédiatement N = 4 . Il y avait donc 2N = 8 paysans. Il ne nous reste plus qu’à réfléchir sur le cas
où on supposerait que le champ B est celui qui a été terminé en premier. C’est inutile,
comme on va le voir tout de suite, mais nous le ferons tout de même par acquit de
conscience et pour bien montrer à quel point l’algèbre est capable de raisonner à
notre place. En effet, si c’était ce scénario qui prévalait, le champ B nécessiterait N
demi-journées de travail et le champ A en nécessiterait 2N + N + 2 ; l’équation serait
donc : 3N + 2 = 2 N … ce qui finirait évidemment par donner N + 2 = 0, c’est-à-dire
N = -2 et nous conduirait dans un monde véritablement difficile à comprendre !

Il reste maintenant une seule question : y a-t-il une solution de nature
arithmétique à ce problème que nous avons été forcés de traiter par l’algèbre ?
Comme je l’ai laissé entendre précédemment, la réponse est « bien sûr que oui ! ».
Mais la solution est difficile à trouver, et ceci pour deux raisons qui nous apparaissent
désormais en pleine lumière grâce à l’équation que nous avons rencontrée tout à
l’heure sous la forme : 3N = 2(N + 2)… Rappelons en effet, que la méthode
élémentaire de « remontée des opérations » ne peut guère fonctionner ici car
l’inconnue N figure dans les deux membres qui traduisent directement les indications
de l’énoncé. Il nous faut donc trouver une façon de « mettre en musique » en langue
naturelle une démarche de résolution de cette équation et, pour être tout à fait
convaincants, il nous faut trouver en outre un cheminement qui puisse, sur le plan de
la narration, être raccroché à l’histoire et à la logique du scénario adopté par
l’énoncé. Je laisse chacun se montrer créatif à sa mesure. Je proposerai simplement
la solution suivante qui consiste à conserver l’équation sous la forme initiale
2N + N = 2(N + 2) et à regrouper de manière astucieuse les demi-journées de travail
effectuées par les paysans, tout en gardant en permanence à l’esprit que le champ A
est le double du champ B :

« Après la première demi-journée, une portion A’ du champ A [dont la surface
correspond à 2N demi-journées] a été récoltée. Elle est naturellement le double de la
portion B’ du champ B qui a été récoltée l’après-midi [qui correspond, elle, à N demi-journées].
Donc comme le champ A est le double du champ B, la portion A" restante
du champ A est encore le double de la portion restante B" du champ B. Mais A"
nécessite N demi-journées [effectuées le premier après-midi] et B"nécessite
seulement les 2 demi-journées effectuées le lendemain ; nous pouvons donc en
conclure que N est le double de 2… ».

Cette façon de relire les choses implique au passage que ce n’est pas B" qui peut
être nulle, et cela montre donc par le raisonnement que c’est bien le grand terrain
dont la récolte est achevée le premier jour. Mais j’espère surtout, après cela, vous
avoir convaincu que ce problème ne peut pas sérieusement être proposé à des CM2,
si ce n’est pour détecter quelque futur académicien. Il nous reste la question
beaucoup plus terre à terre : que faut-il envisager comme apprentissage réaliste au
niveau du primaire ? avec même, parce qu’elle n’est pas forcément illégitime, la
question subsidiaire : ne serait-il pas possible de faire progresser les élèves pour
qu’ils parviennent aussi à résoudre les problèmes chinois ? Il me semble que les deux
problèmes précédents (laitière et terrains chinois) permettent de tirer quelques éléments pour la réflexion sur l’apprentissage. Il s’agit de ma propre religion sur la
question et comme je ne prétends nullement avoir « démontré » ce que je vais
développer, j’essaierai d’indiquer au fil de l’analyse les présupposés de celle-ci.

1°) La difficulté épistémologique.

L’exemple du problème chinois est typique de ce que l’on peut considérer comme
un problème difficile mais élémentaire : la solution « arithmétique » ne met en jeu
aucun outil mathématique autre que la multiplication et la division par deux ! Mais
quel type de démarche permet donc de trouver cette solution ?

Il y a au moins deux types d’obstacles à franchir pour prétendre trouver en restant
dans le cadre élémentaire :
 une excellente capacité de lecture, qui suppose non seulement du déchiffrage et
non seulement un accès au « sens » au niveau de la langue naturelle, mais aussi une
faculté d’extraire de l’énoncé une vision « experte » de la situation racontée :
élimination des informations inutiles (haricots verts, paysannerie, etc., et même
nombre d’heures de travail par journée…), reconstruction de la situation-problème
sous forme pertinente ;
 une capacité à trouver une solution dans un labyrinthe dont la sortie suppose un
nombre assez conséquent d’étapes à franchir et à enchaîner de façon non seulement
logique mais aussi de façon suffisamment efficace pour que les calculs débouchent
réellement sur le résultat cherché. Il faut de la chance : c’est ce que l’on a depuis
toujours appelé la « bosse des maths » !

Cette dernière compétence s’apprend-elle ? Je l’ignore. Elle suppose, je pense,
une manière de réfléchir très synthétique, très géométrique, très imaginative, très
intuitive, car elle consiste à véritablement trouver un chemin alors que l’on ne
dispose pas (par hypothèse) d’une connaissance préalable de la situation. À
l’opposé, pourrait-on dire, de ce genre d’appel à l’astuce pure, on peut placer les
démarches que j’ai exposées jusqu’ici : elle reposent avant tout sur un métier et sur
des outils qui ont été forgés pendant des siècles.

Considérons par exemple la technique de mise en équation, dont j’espère avoir
convaincu qu’elle pense à notre place. Elle permet de résoudre très efficacement
aussi bien le problème de la laitière que celui du paysan chinois. Elle apporte même
(on l’aura peut-être remarqué au passage) une façon de structurer les données de
l’énoncé qui ne peut qu’aider, sinon à trouver la solution arithmétique, du moins à
dégager des « atomes » de situation qui peuvent souffler les étapes à parcourir. Ce
sont les propositions entre crochets dans ma présentation de la solution arithmétique ;
elles sont inutiles à la rédaction elle-même, mais elles montrent que les jalons
essentiels sont présents dans la démarche d’algébrisation. De même, les diverses
méthodes que j’ai présentées au titre de solution arithmétique pour le problème de la
laitière font appel à un métier qui a certes nettement vieilli, qui est beaucoup moins
performant que la méthode algébrique au sens où il n’offre pas de démarche
« universelle » et susceptible d’une puissance analytique insoupçonnée, mais qui
n’en est pas moins un véritable « métier ». Il consiste à faire appel à un type un peu différent d’intuition : la mémoire, l’esprit d’analogie, le sens de l’adaptation, qui sont
autant de compétences permettant de rapprocher une situation nouvelle de situations
déjà traitées et résolues, entreposées dans une sorte de bibliothèque cérébrale…

Nous avons donc affaire, sur les deux exemples précédents, à deux types
d’intelligence et aussi à deux types d’outils. En matière d’intelligence, nous pouvons
en effet nous rappeler que les Grecs avaient, dans leur mythologie, deux déesses
consacrées à l’intelligence. L’une, Métis, correspondait à l’intuition qui relève du
talent, de la ruse, mais aussi de l’expérience acquise, du métier, et qui semble
fonctionner de manière non formalisable, difficilement explicitable et difficilement
transmissible. L’autre, Athéna, personnifiait au contraire l’intelligence industrieuse,
méthodique, formalisable… Je pense qu’il n’est pas besoin de préciser le type de
parallèle que j’aimerais faire entre ces deux figures et les exemples qui précèdent.
Mais ce sur quoi je voudrais surtout insister, tient dans la remarque suivante : je crois
assez fermement que seule la deuxième forme d’intelligence ainsi schématisée est
susceptible de relever de la réflexion sur l’École, que seuls les méthodes et les outils
que nous avons rencontrés jusqu’ici sont susceptibles d’être transmis à l’élève et que
c’est un défi tout à fait légitime – et suffisamment difficile – que de chercher à
transmettre ce genre de compétences dans le cadre de notre enseignement.

C’est à cela que je ferai référence quand je parlerai « d’instruction » dans la
suite… Et la question qui reste est ainsi un peu précisée mais toujours la même :
comment est-il possible d’enseigner mieux à ce niveau ? Une première décision à
prendre concerne le choix du type d’outil qu’il est préférable d’enseigner : méthodes
« arithmétiques » ou méthodes « algébriques » ? ou si l’on préfère : méthodes
« techniciennes » ou méthodes « savantes » ?

Concrètement, c’est une véritable question qui ne me semble pas complètement
avoir sa réponse dans l’histoire. J’ai déjà expliqué quel était le choix des maths
modernes et on peut évidemment s’intéresser aux choix antérieurs à cette période,
seulement ceux-ci ne s’appliquaient pas à une situation de type « collège unique ».
Si bien que le « niveau de culture primaire » d’avant les mathématiques modernes est
quelque chose d’assez hybride, assez bien résumé dans l’exemple du problème de la
laitière qui s’annonce comme « niveau CM2 – certificat d’études ». On peut admettre
que les élèves acceptés en sixième étaient ceux qui avaient acquis en fin de CM2 le
niveau de ce type de problèmes, mais on peut penser aussi que la plupart des élèves
qui entraient au collège ne l’avaient pas réellement. Alors même que, au contraire,
les problèmes difficiles et résolus par l’arithmétique étaient prétendument destinés
aux fin d’études, pendant que les élèves entrés au collège découvraient assez vite la
méthode algébrique. (C’est en tout cas ce qui se passait dans les années 50).

La situation actuelle du collège unique amène de toutes façons à se poser le
problème différemment, et sous un angle purement épistémologique : que faire de la
résolution des problèmes « par l’arithmétique » alors que tous les enfants sont
destinés à suivre le même cursus qui doit leur faire aborder les méthodes de
résolution par l’équation ? Disons à partir de la quatrième. Ce « stade » doit-il
légitimement exister ? ou, au contraire : « peut-on légitimement se priver d’un tel
stade avant d’aborder le passage à l’algèbre ? ».

J’ai déjà dit que ma position personnelle est plutôt qu’il n’est pas sérieux
d’aborder l’algébrisation sans avoir rencontré des méthodes de résolution de type
arithmétique. Je pense qu’en réalité la vraie difficulté est de doser de manière
pragmatique le type de problèmes que l’on doit apprendre à surmonter dans ce que
j’ai appelé le « niveau de culture primaire » et qu’il est bon que les enfants
rencontrent les méthodes de mise en équation après avoir acquis une certaine
habitude de réflexion sur des problèmes de type « concret ». C’est en ce sens que j’ai
voulu parler de « rupture – chevauchement ». Mais cela dit, que proposer comme
corpus de problèmes à rencontrer en primaire ou en début de collège ? Ici encore il
ne peut être question que de pragmatisme … et d’un pragmatisme qui prenne en
compte aussi bien les capacités des élèves que celles des maîtres. On m’accordera
sans réticences, je l’espère, la possibilité d’écarter le problème des deux terrains de
l’enseignement « obligatoire ». On m’accordera à l’inverse le choix d’y mettre tous
les problèmes qui relèvent directement de ce que l’on peut appeler l’acquisition du
« sens des opérations », avec comme seules restrictions un dosage pertinent au
niveau de la complexité des nombres rencontrés et au niveau des situations concrètes
mises en jeu. Reste la question de tous les problèmes intermédiaires ! Disons, de ce
qui relève de la proportionnalité à ce qui peut déboucher sur les « fausses
suppositions », en passant par des problèmes-types plus ou moins paradigmatiques
mettant en jeu par exemple les pourcentages, les vitesses, les mélanges, etc.

2°) Quels choix retenir ?

La tendance actuelle au niveau de l’enseignement primaire me semble reposer sur
trois grandes idées directrices :
 l’atténuation des apprentissages « algorithmiques » tels que celui de la division,
 l’allongement des apprentissages de l’école jusque vers la fin de la cinquième, ce
qui revient à fixer le niveau « fin de primaire » à ce stade,
 la mise en place d’activités destinées à ce que l’élève « construise lui-même » ses
propres procédures à partir de diverses « situations – problèmes »…

Le premier point est pour moi relativement mystérieux et je ne voudrais pas
déborder mon sujet en essayant de le traiter ici, le second point est précisément au
cœur de notre sujet. Ce type d’objectif n’est pas nécessairement dramatique en lui-même
si on conserve pleinement la gestion d’un véritable « niveau de culture ».
C’est
sans doute une obligation qu’il convient d’assumer enfin dans le cadre du collège
unique et c’est peut-être une façon efficace de prendre en charge plus en douceur les
élèves moyens. Nous vivions plutôt jusqu’ici dans l’idée d’une fin de primaire qui
devait correspondre à un véritable stade dans les apprentissages (évaluations à
l’entrée en sixième) et, surtout, dans l’idée que la sixième devait constituer une sorte
de « rupture » permettant aux enfants de « revisiter » les savoirs du primaire sous un
éclairage préparant aux programmes du collège. Mais dans la mesure où la question
se pose désormais de bien mesurer ce qui peut effectivement constituer un niveau de
culture primaire, il n’est pas interdit de considérer que ce « niveau primaire » ne
demande pas plus d’être établi en fin de cours moyen, qu’en section de « fin
d’études » … ou qu’en fin de cinquième. Et on aura compris que la seule question qui vaille en ce qui concerne la résolution de problèmes est dans la manière de gérer
la transition entre l’approche « arithmétique » et l’approche « algébrique ».

Cette question ne me semble pas pouvoir être dissociée du troisième point rappelé
plus haut concernant la construction des « procédures » de résolution par l’élève.

C’est ce troisième volet qui me semble le plus discutable. Il sacrifie sciemment
ce que l’on peut regarder comme une forme d’apprentissage « procédural » à ce que
l’on croit – ce que l’on espère – être une piste plus efficace d’acquisition du « sens ».
Je pense personnellement que c’est une erreur, car je ne crois pas que le mot « sens »
puisse recouvrir ici autre chose que la maîtrise de savoir-faire et parce que je crois au
contraire que c’est l’accumulation d’une expérience dans un grand nombre de
problèmes qui permet ensuite, par analogie, de pouvoir réagir dans des situations
plus ou moins nouvelles.

Le « constructivisme » des mathématiques modernes qui rêvait de voir les enfants
réinventer eux-mêmes la théorie des ensembles et pénétrer ainsi directement dans les
arcanes des mathématiques les plus sophistiquées a laissé la place à une autre forme
de constructivisme tout aussi illusoire. On s’imagine désormais que « l’activité » sur
quelques problèmes plus ou moins ouverts va permettre aux élèves de (se) forger des
outils personnels qu’il sauront « réinvestir » dans d’autres configurations. On se
trompe lourdement. On croit par exemple préparer les élèves à des tas de
« compétences » plus ou moins transversales qui ne pourront que lui être utiles dans
ses études mathématiques futures : conjecturer, analyser, démontrer – et que sais-je
encore ? – en le confrontant à la recherche du nombre de lapins et de scarabées dans
une population dont on connaît le nombre d’individus et le nombre total de pattes…

Mais comment veut-on que ce type d’activité de recherche autour d’un problème
du type « fausses suppositions » puisse servir à quoi que ce soit, si elle ne débouche
pas sur la mise en place d’exercices systématiques et répétitifs. Pense-t-on vraiment
que l’élève va réinventer la méthode ? Pense-t-on vraiment que, plus tard, il ait une
chance de reconnaître une situation analogue s’il n’a pas été entraîné à cette
reconnaissance ? Non bien sûr. On pense naïvement que les « compétences »
mathématiques sont de « conjecturer », « d’analyser », de « démontrer », etc., et que
l’on peut, pour cela, faire l’économie d’une progression et surtout des savoir-faire,
des méthodes, des techniques, qui seraient à reléguer au rayon des vieilleries.

C’est malheureusement contraire à toutes les observations de bon sens. D’un côté
tout enseignement un peu spécialisé dans les finalités techniques suppose un
apprentissage capable de conduire l’élève à maîtriser des ressources que personne ne
songerait à lui demander de réinventer. De l’autre les meilleurs spécialistes des
disciplines concernées sont les premiers à expliquer qu’ils n’ont acquis leur
excellence, pour ne pas dire leur génie, qu’à force d’acquisitions progressives,
systématiques, voire répétitives, mais menées de façon intelligente par l’école !

Quelle élite illusoire prétend-on donc former, alors que l’on n’enseigne presque
plus de ces savoirs de base qui sont seuls susceptibles de fournir une expérience
véritable, un soubassement sérieux et efficace pour les études futures ? Problèmes de proportionnalité ? Il suffira que l’élève invente lui-même règle de trois, produit en
croix, fractions et autres pourcentages ! Problèmes de vitesses ? Il suffira que l’élève
se construise peu à peu la notion de rapport, les formules fondamentales et les unités-quotients
 ! Les manuels actuels du cours moyen sont l’exact opposé des manuels de
naguère. Là où l’on apprenait des savoir-faire (oubliés aujourd’hui) du type de celui
qui est nécessaire pour résoudre le problème de la laitière, on trouve désormais des
« tableaux récapitulatifs » sur la proportionnalité qui mettent, en vrac, sous le nez de
l’élève toutes les variantes d’approches possibles, c’est-à-dire en vérité tout
l’apprentissage envisageable jusqu’à la fin du collège : tableau de proportionnalité,
représentations graphiques, etc., etc.

Les nouveaux programmes de collège, pour peu qu’ils aient les moyens de
s’appuyer sur des acquis efficients introduits par l’école primaire – je veux dire des
acquis très élémentaires, mais assurés –, les programmes de collège, donc, ont peut-être
actuellement la possibilité d’apporter, en sixième - cinquième une véritable
« culture primaire ». Il suffirait pour cela que les penseurs de l’école ne se contentent
pas de croire qu’ils doivent former des chercheurs … et que cela se réalise
uniquement en cherchant ! Au contraire.

Les deux premières années du collège pourraient alors parachever l’apprentissage
du sens des opérations (supposé déjà introduit dans des situations claires et simples)
tout en enrichissant petit à petit le champ numérique mis en jeu par des énoncés plus
complexes. Elles auraient aussi la possibilité de gérer de façon maîtrisée la
complexification des domaines auxquels les méthodes de résolution peuvent
s’étendre et — pourquoi pas dans le cadre d’une pédagogie différenciée — elle
pourrait parallèlement initier les élèves les plus doués à des questionnements sur des
problèmes plus astucieux ou plus spécialisés.

Les problèmes de la vie courante ne manquent pas pour constituer un fonds
utilisable en début de collège pour illustrer l’introduction des nombres décimaux, des
nombres relatifs, des fractions, des pourcentages, etc. Ils sont proposables à tous les
élèves si l’on sait en doser les difficultés et prendre le temps de les visiter pour eux-mêmes.
Et ce serait une erreur de croire que les « bons » élèves n’ont rien à en
apprendre de mathématique. On ne mesure sans doute plus la valeur formative de
« petits problèmes » ou de « petites techniques », quand bien même il ne s’agirait que
de problèmes de laitière ou de paysans chinois. On se leurre sur l’apprentissage du
sens en oubliant que « faire comprendre » quelque chose, comme le disait très bien
Henri Lebesgue en 1939, « c’est essentiellement l’intégrer dans un tout cohérent dont
certaines parties sont déjà bien familières »… et que cela suppose de s’être
familiarisé auparavant avec des domaines que l’on a l’impression de maîtriser !

On semble même ignorer le plaisir qu’il peut y avoir, pour esprit un peu vif, à
jongler avec des outils aussi magiques, aussi ésotériques et aussi « démodés » que la
« croix des mélanges ». Le « raisonnement » se limite certes à la maîtrise d’un
algorithme simple, combinatoire et très visuel, mais comment ne pas voir que le seul
fait de savoir l’adapter à des situations plus ou moins inattendues est précisément le
ressort essentiel des esprits scientifiques ? Comment ne pas ressentir l’attrait des « comment ça marche ? » que de telles rencontres peuvent susciter ? Comment ne
pas mesurer le plaisir et l’intérêt que peut entraîner le simple fait de revisiter plus tard
ce genre de savoirs en termes de proportionnalité, de barycentres ou même de
formules algébriques sophistiquées ?

L’École va mal aujourd’hui pour de nombreuses raisons. D’abord, sans doute,
parce que la société va mal et qu’elle a un peu trop tendance à exiger de l’École
qu’elle règle tous ses problèmes. Ensuite, certainement, parce que les évolutions
culturelle et sociale se sont ingéniées à relativiser largement l’intérêt des études
comme moteur de l’ascenseur social. Enfin, et surtout, il faut bien le reconnaître en
ce qui concerne les sciences et les mathématiques, parce que les errements en matière
de programmes nous ont conduits à ne plus savoir quoi enseigner, ni comment.

Dans cette situation, le début du collège échappera de moins en moins à un destin
qu’il s’est employé à retarder le plus longtemps possible depuis l’avènement du
collège unique. Il est, au moins jusqu’au seuil de la quatrième, le véritable cycle qui
doit correspondre à la « fin des études primaires ». Cela le place devant deux types
de défis : le premier est de parvenir à prendre en compte – et à faire fructifier – une
diversité des élèves dont il parvient de moins en moins à se préserver artificiellement,
le second est d’assumer et, ici aussi, de parvenir à tirer profit d’un programme qui
doit permettre à tous les élèves d’acquérir une culture minimale, tout en offrant aux
meilleurs un bagage attrayant et enrichissant pour leurs études secondaires. On
tenté, il y a trente cinq ans, de gérer l’apprentissage des sciences comme s’il suffisait
de décréter une révolution scientifique. Peut-être le temps est-il enfin venu de
commencer à reprendre sérieusement la question, en cessant d’une part de se fixer
des buts inaccessibles et, d’autre part, d’idéaliser désespérément le passé…