Exercices

Exercice 461-1

Trouver les valeurs entières de x et de y qui satisfont aux deux équations :

$$\left \{ \begin{array}{r c l} x^3 + y^3 &=& 468 \\ x^5 + y^5 &=&19932 \end{array} \right.$$

(Charles de Comberousse 1923)

voir l’article où est publiée la solution

Exercice 461-2

« La somme des volumes des pyramides ayant pour bases les faces latérales d’un prisme et pour sommet commun un point quelconque intérieur au prisme, est constante. Dans quel rapport est-elle avec le volume du prisme ? »

(Jacques Hadamard – Leçons de géométrie élémentaires – Armand Colin 1901)

voir l’article où est publiée la solution

Exercice 461-3 Corol’aire n^o 32 (Mars 1998 – page 6)

Curiosités :

1. Calculer 8 589 934 592 × 116 415 321 826 934 814 453 125 (Ogilvy-Anserson)
2. Calculez à la machine le nombre

   $$ n= \left [ ln \left( \dfrac {640320^3+744}{\pi}\right) \right ] ^{2} .$$

Si le résultat vous surprend — ce qui serait normal ! — alors consultez, à la page 100, le merveilleux bouquin de François Le Lionnais, « Les nombres remarquables » (Éditions Hermann 1983).

Exercice 461-4 (proposé par Gérard Macombe, IPR à Rennes).

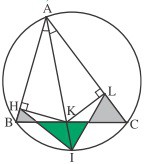
ABC est un triangle inscrit dans un cercle. La bissectrice de l’angle $\widehat{BAC}$ coupe le cercle en I et [BC] en K. H et L sont les projetés orthogonaux de K sur (AB) et (AC).
Comparer l’aire du triangle vert à la somme des aires des deux triangles gris.

Miguel Amengual Covas nous signale que c’est le problème n^o 2 de la 28^e olympiade internationale de mathématiques à Cuba en 1987.

voir l’article où est publiée la solution

Solutions

Exercice 455-2 Proposé par Jacques Chayé, de Poitiers

Soit ABC un triangle quelconque. Soient A′, B′ et C′ les pieds des hauteurs respectivement sur (BC), (CA) et (AB) ; soit I, J et K les milieux respectifs de [BC], [CA] et [AB] ; soit U, V et W les milieux respectifs de [AA′], [BB′] et [CC′]. Démontrer que les droites (IU), (JV) et (KW) passent par un même point.

Solution de Georges Lion (Mata Utu – Wallis)

Exercice 457-2 – Proposé par Madame Fathi Drissi (Comité de la Régionale APMEP de Lorraine)

1. À l’aide du seul compas, construire le centre d’un triangle équilatéral dont on connaît les sommets A, B et C.
2. À l’aide du seul compas, construire un point situé au tiers d’un segment [AB] donné.

Solution de Jean-Claude Carréga (Lyon)

Solution de Michel Blévot (Saint-Denis de la Réunion)

Autres solutions : de R. Raynaud (à l’aide de l’inversion) et A. Corée (à l’aide de la symétrie).

Rappel : Article de Jacques Fort « La géométrie du compas », BV n^o 376 de Décembre 1990, article citant par ailleurs Jean-Claude Carréga : « La règle, le compas et la théorie des corps », BV n^o 315 de septembre 1978.

Une information :
Robert Vidal, de Narbonne, nous signale qu’on peut télécharger, sur le site du rectorat de Montpellier, un document « Mathematica Dinosaurus » (Morceaux choisis) de Jean-Marc Dewasme contenant de nombreux problèmes du style de ceux de cette rubrique. Vous le trouverez à l’adresse suivante :
http://pedagogie.acmontpellier.fr/Disciplines/maths/pedago/dewasme/MathematicaDinosaurus.pdf