478
L’évaluation des compétences mathématiques dans l’enseignement secondaire obligatoire en Espagne
Richard Cabassut
Les textes officiels français [1] précisent que « La définition du socle commun prend
[...] appui sur la proposition de recommandation du Parlement européen et du Conseil
de l’Union européenne en matière de “ compétences-clés pour l’éducation et
l’apprentissage tout au long de la vie ”. Elle se réfère [...] aux évaluations
internationales, notamment au Programme international pour le suivi des acquis des
élèves (PISA) qui propose une mesure comparée des connaissances et des compétences
nécessaires tout au long de la vie ». Effectivement se mettent en place dans différents
pays d’Europe des dispositifs présentant des analogies avec le socle commun français :
les huit compétences mathématiques au Danemark en 2002 avec le programme KOM
piloté par Mogens Niss qui inspirera et animera PISA, les « Bildungsstandards » en
Bade-Wurtemberg en 2004 et en Autriche en 2006, les « functionnal skills » en
Angleterre expérimentés à partir de 2007, les « enseñanzas mínimas y competencias
básicas » en Espagne dans la réforme de l’ESO de 2006, … Nous allons étudier plus
en détail ce dernier dispositif pour nous permettre de prendre de la distance par rapport
à la mise en place du socle commun en France et mieux le questionner, notamment
quant à son évaluation.
1. Les « enseignements minimaux » en Andalousie
- 1.1 Décentralisation du système éducatif
Depuis l’adoption de la nouvelle constitution de 1978, le système éducatif a opéré un
transfert des fonctions, des services et des ressources de l’État Central aux
Communautés Autonomes, qui peuvent avoir en plus du castillan une autre langue
officielle d’enseignement (comme par exemple le catalan en Catalogne). Cette
décentralisation répartit les compétences entre l’État Central, les Communautés
Autonomes, les administrations locales et les établissements scolaires. Des décrets
royaux peuvent harmoniser les systèmes de chaque Communauté Autonome. Nous
allons nous limiter à l’exemple de la Communauté Autonome d’Andalousie.
La scolarité obligatoire, de 6 à 16 ans, débute à l’école primaire pendant 6 ans, des
classes 1 à 6. Elle se poursuit 4 ans à l’école secondaire, des classes 1 à 4. L’école secondaire non obligatoire, après 16 ans, est composée des classes 1 et 2. - 1.2 Un cadrage national des enseignements minimaux
Le décret royal du 29 décembre 2006 fixe un cadre commun à toutes les
Communautés pour les enseignements minimaux de l’éducation secondaire
obligatoire dans les termes suivants.
Les enseignements minimaux sont les aspects de base du curriculum référés aux
objectifs, aux compétences de base, aux contenus et aux critères d’évaluation.
L’objectif du décret royal est d’établir les enseignements minimaux de l’éducation
secondaire obligatoire.
La finalité des enseignements minimaux est d’assurer une formation commune à tous
les élèves du système éducatif dans le système scolaire espagnol et de garantir la
validation des diplômes correspondants.
65% de l’horaire doit être alloué au curriculum minimal [55% dans les régions où
existe une seconde langue officielle, comme par exemple la Catalogne]. Le reste est
attribué au projet éducatif des établissements scolaires.
À partir de la troisième année, il y a une possibilité de diversification pour permettre
à chaque élève d’atteindre les objectifs et d’obtenir le titre de diplômé de
l’enseignement secondaire obligatoire.
Les programmes de l’éducation professionnelle sont destinés aux élèves qui n’ont pas
obtenu ce diplôme ; ils leur offrent la possibilité de l’obtenir par une préparation
spéciale.
De même sont établis les principes d’une préparation spéciale à ce diplôme destinée
aux adultes.
À la fin de la deuxième année, une évaluation diagnostique à valeur formative et
d’orientation permet à chaque élève de déterminer les moyens adéquats d’amélioration
pour achever son éducation secondaire obligatoire. - 1.3 Place des mathématiques dans l’enseignement secondaire obligatoire (12 à 16 ans)
Les matières obligatoires au cours des trois premières années sont : sciences
naturelles ; sciences sociales ; histoire et géographie ; éducation physique et sportive ;
espagnol et littérature (et éventuellement langue régionale officielle) ; langue
étrangère ; mathématiques. S’y ajoutent au plus deux matières supplémentaires
parmi : éducation à la citoyenneté et aux droits de l’homme ; éducation plastique et
visuelle ; musique ; technologie.
Pour la quatrième année sont obligatoires : sciences sociales ; histoire et géographie ;
éducation éthique et civique ; espagnol et littérature (et éventuellement langue
régionale officielle) ; première langue étrangère ; mathématiques. Trois matières
supplémentaires sont à choisir parmi : biologie et chimie ; éducation plastique et
visuelle ; physique et chimie ; latin.
En mathématiques il y a un cours unique lors des trois premières années et une
différenciation en quatrième année entre un cours propédeutique à la poursuite d’études
mathématiques et un cours terminal. L’horaire mathématique est environ 20% de
l’horaire total, soit 280 heures pour les trois premières années et 105 heures pour la
quatrième.
- 1.4 L’évaluation de la responsabilité de chaque professeur
Dans l’établissement scolaire, l’évaluation est de la responsabilité des professeurs
(contrôle continu et/ou tests de fin d’année en juin, éventuellement dans certaines
écoles rattrapage en septembre).
L’évaluation de l’élève est continue. Elle est différenciée suivant les matières choisies
mais les mathématiques sont obligatoires, donc toujours évaluées.
À partir de la troisième année, les établissements scolaires peuvent organiser des
programmes curriculaires diversifiés adaptés aux besoins de certains élèves.
Le passage en classe supérieure n’est pas possible si l’évaluation est négative dans au
moins trois matières. Le droit au redoublement existe jusqu’à l’âge de 18 ans.
À la fin de l’enseignement secondaire obligatoire, le diplôme de l’enseignement
secondaire obligatoire est attribué par un conseil de professeurs. - 1.5 La compétence mathématique en Espagne
Il semble intéressant de comparer la compétence mathématique définie en France pour
le socle commun avec celle définie dans le décret royal précité en les termes suivants.
La compétence mathématique consiste en l’aptitude à utiliser et à mettre en rapport
les nombres, leurs opérations de base, les symboles et les formes d’expression et de
raisonnement mathématique, tant pour produire et interpréter différents types
d’information, que pour étendre la connaissance sur les aspects quantitatifs et spatiaux
de la réalité, et pour résoudre des problèmes en rapport avec la vie quotidienne et avec
le monde du travail.
Fait partie de la compétence mathématique l’aptitude à interpréter et à exprimer avec
clarté et précision des informations, des données et des argumentations, qui augmente
la possibilité réelle de continuer à apprendre tout au long de la vie, tant dans le cadre
scolaire ou académique comme en dehors, et favorise une réelle participation réelle à
la vie sociale.
De même cette compétence implique la connaissance et le maniement des éléments
mathématiques de base (différents types de nombres, mesures, symboles, éléments
géométriques, etc.) dans des situations réelles ou simulées de la vie quotidienne, et la
mise en pratique de processus de raisonnement qui aboutissent à la résolution des
problèmes ou à l’obtention d’information. Ces processus permettent d’appliquer cette
information à une plus grande variété de situations et de contextes, de suivre des
chaînes d’argumentation en identifiant les idées fondamentales, et d’estimer et de juger
la logique et la validité des argumentations et informations. Par conséquent, la
compétence mathématique suppose l’aptitude à suivre certains processus déterminés
de pensée (comme, entre autres, l’induction et la déduction) et à appliquer quelques
algorithmes de calcul ou des éléments de logique, ce qui conduit à identifier la validité
des raisonnements et à évaluer le degré de certitude associé aux résultats dérivés des
raisonnements valables.
La compétence mathématique induit une disposition favorable et une sécurité et une
confiance progressives envers l’information et les situations (problèmes, inconnues,
etc.) comportant des éléments ou des supports mathématiques, ainsi que leur
utilisation quand la situation l’indiquera, basée sur le respect et le goût de la certitude
ainsi que sur la recherche de celle-ci à travers le raisonnement.
Cette compétence apporte réalité et sens à l’utilisation des éléments et des
raisonnements mathématiques pour faire face aux situations quotidiennes qui la
nécessitent. Par conséquent, l’identification de telles situations, l’application de
stratégies de résolution de problèmes et le choix de techniques adéquates pour calculer,
représenter et interpréter la réalité à partir de l’information disponible en font partie.
Pour cette raison, son développement dans l’enseignement obligatoire sera atteint
dans la mesure où les connaissances mathématiques sont appliquées de manière
spontanée à une grande variété de situations provenant d’autres domaines de
connaissance et de la vie quotidienne. Le développement de la compétence
mathématique à la fin de l’éducation obligatoire implique d’utiliser spontanément - dans les domaines personnel et social – les éléments et les raisonnements
mathématiques pour interpréter et produire de l’information, pour résoudre des
problèmes provenant de situations quotidiennes et pour prendre des décisions. En
définitive, cela suppose d’appliquer des aptitudes et attitudes permettant de raisonner
mathématiquement, de comprendre une argumentation mathématique, de s’exprimer et
de communiquer dans le langage mathématique, en utilisant pour cela les outils
adéquats, et en intégrant la connaissance mathématique à d’autres types de
connaissance pour fournir une meilleure réponse aux situations de la vie de différents
niveaux de complexité. - 1.6 Critères d’évaluations
Après les blocs de programmes un certain nombre de critères d’évaluations sont
explicités pour chaque année.
Nous en donnons à titre d’exemple quelques-uns relatifs à la deuxième année.
Critères d’évaluation
- 1 Utiliser des nombres entiers, des fractions, des décimaux et des pourcentages
simples, leurs opérations et leurs propriétés, pour rassembler, transformer et échanger l’information et résoudre des problèmes en rapport avec la vie quotidienne. Il s’agit
d’évaluer la capacité à identifier et à employer les nombres et les opérations en étant
conscient de leur signification et de leurs propriétés, à choisir la forme de calcul
appropriée (mental, écrit ou à la calculatrice) et à juger de la cohérence et de la
précision des résultats obtenus. En ce qui concerne les opérations auxquelles se réfère
ce critère, il convient d’y inclure les puissances d’exposant naturel. Il est d’une
importance particulière d’évaluer l’utilisation de différentes stratégies permettant de
simplifier le calcul avec des fractions, décimaux et pourcentages, ainsi que l’aptitude
à appliquer ces calculs à une vaste variété de contextes. - 2. Identifier des relations de proportionnalité numérique et géométrique et les utiliser
pour résoudre des problèmes dans des situations de la vie quotidienne. Il s’agit de
vérifier la capacité d’identifier, dans différents contextes, une relation de
proportionnalité entre deux grandeurs. De même, il s’agit d’évaluer la capacité à
mettre en œuvre différentes stratégies (utilisation de tableaux, obtention et utilisation
de la constante de proportionnalité, réduction à l’unité, etc.) pour obtenir des éléments
inconnus dans un problème à partir d’autres connaissances, dans des situations de la
vie réelle où il existe des relations de proportionnalité.
(…) - 7. Utiliser des stratégies et des techniques de résolution de problèmes, comme
l’analyse de l’énoncé, essai et ajustement, la division du problème en sous-problèmes,
ainsi que la vérification de la cohérence de la solution obtenue, et exprimer, en
utilisant un langage mathématique adapté à ce niveau, la procédure qui a été suivie
dans la résolution. Ce critère permet d’évaluer la façon de faire face à des tâches de
résolution de problèmes pour lesquels on ne dispose pas d’une procédure standard
permettant d’obtenir la solution. Ceci va de la compréhension de l’énoncé à partir de
l’analyse de chacune des parties du texte et de l’identification des éléments les plus
significatifs, jusqu’à l’application de stratégies de résolution, ainsi qu’à l’habitude et
à l’aptitude nécessaires pour vérifier la correction de la solution et sa cohérence avec
le problème posé. Il s’agit de même d’évaluer la persévérance dans la recherche de
solutions et la confiance en ses capacités pour l’obtenir, ainsi que la capacité à
transmettre, avec un langage suffisamment précis, les idées et les processus
personnels développés, de façon à se faire comprendre et à être compris de ses
camarades.
- 1 Utiliser des nombres entiers, des fractions, des décimaux et des pourcentages
- 1.7 Sujets d’évaluations diagnostiques communs à toute l’Andalousie
En mathématiques, il existe deux évaluations avec le même sujet pour toute
l’Andalousie : une au milieu de l’enseignement primaire (de 6 à 12 ans), et une au
milieu de l’enseignement secondaire obligatoire (de 12 à 16 ans). L’évaluation
régionale dans le secondaire se situe en général au début de la troisième année. Pour
l’élève, elle est diagnostique et formative (mise en place de soutien, aide à
l’apprentissage, …) ; elle aide à l’orientation de l’élève ; elle permet enfin d’avoir une
vue systémique de l’enseignement des mathématiques à ce niveau.
Voici deux extraits du sujet d’évaluation diagnostique d’octobre 2006. - 1.7.1 Les nombres
Situation-problème : chez le marchand de fruits
Question 1 :
La mère des frères Jean et Antoine leur demande d’effectuer les achats suivants chez le
marchand de fruits et légumes :
1/2 kg de carottes à 0,70 /kg,
1/4 kg de piments à 2,20 /kg,
1kg et 1/2 d’oranges à 0,80
1 kg et 3/4 de pommes à 1,40 kg.
Quel est le poids total des produits achetés ? Explique comment tu obtiens le résultat.
| Question 1 | Compétence | Organiser, comprendre et interpréter l’information. | Élément de compétence | Identifier le sens de l’information numérique et symbolique. |
| Contenu | Nombre et mesure. |
| barême : 2 | si la réponse est correcte : 4kg Elle s’obtient au moyen de la somme de toutes les quantités données. On peut obtenir la somme des fractions 1/2 + 1/4 + 1/2 + 3/4 = 8/4 = 2 et ajouter à ce résultat les 2 kg restant. On peut exprimer les fractions en nombres décimaux et les additionner : 0,5 + 0,25 + 1,5 + 1,75 = 4. |
| barême : 1 | On donne la réponse correcte sans argumentation. On n’indique pas les unités. | barême : 0 | 0 Toute autre réponse. |
Question 2 :
La mère pense qu’on a dépensé davantage pour les fruits que pour les légumes. A-t-elle
raison ? Expliquer.
.
| Question 2 | Compétence | Exprimer | Élément de compétence | Justifier les résultats exprimés en exprimant des arguments sur une base mathématique. |
| Contenu | Nombre et mesure. |
| barême : 2 | La réponse correcte est qu’elle a raison parce que le coût des
fruits est
1,5 kg ×0,8 €/kg + 1,75 ×1,4 €/kg = 3,65 €
tandis que le coût des légumes est :
0,5 ×0,7 €/kg + 0,25 ×2,2 €/kg = 0,9 €. Il n’est pas nécessaire que les opérations figurent sous la forme ci-dessus, mais il est suffisant qu’apparaissent les calculs précédents. |
| barême : 1 | On répond qu’elle a raison mais on évoque une argumentation pauvre qui ne repose pas sur les opérations qui doivent être effectuées. | barême : 0 | 0 Toute autre réponse. |
- 1.7.2 Géométrie
Situation-problème : L en construction
Question 7 :
Dans les dessins suivants on montre la construction des quatre premières figures d’une suite utilisant des carreaux noirs.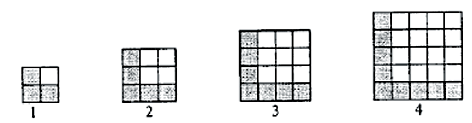
Considérons la question suivante : Combien de carreaux noirs faut-il pour dessiner la
pièce qui occupe la place 100 ?
Pour répondre, on pourra commencer de différentes manières.
Une première manière serait :
Chaque branche du L contient 100 carreaux noirs et on ajoute celui du coin.
Une deuxième manière serait :
Une branche contient 100 carreaux noir et l’autre 101, soit un total de …
Une troisième manière serait :
La figure s’obtient en enlevant à un carré de 101 carreaux de côté un carré de
côté 100 …
Lis attentivement chacune des réponses précédentes et signale celle qui te paraît la
plus simple, en expliquant pourquoi et en complétant pour terminer de répondre à la
question sur le nombre de carreaux noirs nécessaire pour dessiner la pièce qui occupe
la place 100.
| Question 7 | Compétence | Poser et résoudre des problèmes. | Élément de compétence | Apprécier la pertinence de différentes façons de résoudre des problèmes avec une base mathématique. |
| Contenu | Géométrie. |
| barême : 2 | La réponse est 201 parce que :
si on choisit la première manière : 2 × 100 + 1 = 201 ; si on choisit la deuxième manière : une branche a 100 carreaux et l’autre 101 soit un total de 100 + 101 = 201 ; si on choisit la troisième manière : la figure s’obtient en enlevant à un carré de côté 101 un carré de côté 100 : \(101^{2} -100^{2} = 10 201 - 10 000 = 201\). On peut indiquer qu’aucune des manières n’est meilleure qu’une autre. Il faut argumenter si l’une paraît plus simple ; si on utilise le sens commun on considérera la réponse comme valable. |
| barême : 1 | Donne la réponse 201 en justifiant exclusivement la
manière choisie pour calculer. Donne une réponse incorrecte, mais l’argumentation est valide. | barême : 0 | 0 Toute autre réponse. |
Commentaires :
On observe que l’évaluation ne se fait pas sur la seule base de la correction des
traitements ou la seule validité des raisonnements, mais qu’elle prend en compte des
compétences plus larges. L’un des exercices fait appel à une situation de la vie
quotidienne et effectivement, sur les 17 questions de cette évaluation, 14 concernent
des situations en lien avec la réalité, ce qui n’est pas sans rappeler les situations de
l’enquête PISA.
2. Questions
On voit illustré à travers le cas espagnol qui vient d’être exposé et le cas français une
variété de situations dans la mise en place de ces compétences communes : dans des
contextes variés, soit avec une différenciation précoce (comme en Bade-Wurtemberg)
ou tardive comme en France, une décentralisation importante en Espagne ou faible en
France, avec des variétés des conceptions de ce qui est commun et des différences dans
l’évaluation de ces compétences : évaluations locales organisées par les professeurs
ou évaluations communes organisées par une autorité, évaluations pour former, pour
orienter, pour certifier, différence dans les choix des moments de l’évaluation.
Pourtant il apparaît des éléments communs : les mathématiques sont toujours
présentes dans ces compétences communes et elles sont évaluées ; les évaluations
visent à porter une attention particulière aux élèves en difficulté ; le souci de
l’efficacité du système éducatif et le souci d’une formation de base utile pour la vie
quotidienne, professionnelle et citoyenne apparaissent dans la formulation des
compétences et dans leurs évaluations.
Certaines mises en garde se font entendre : « L’École peut prendre l’allure d’une salle
des marchés où, loin des trop longs détours de la connaissance “ théorique ”, on gère
fiévreusement un “ portefeuille des compétences ” qu’il convient d’actualiser
rapidement pour répondre aux demandes des différents marchés sur lesquels l’individu
est censé réaliser sa valeur » [Chevallard 2002, p. 54-55]
Il restera donc, après avoir mis en place et observé ces différents dispositifs, à les
aménager ou à les réformer en fonction des évaluations.
Annexe
Programmes de mathématiques
Nous donnons les extraits suivants du programme de mathématiques du cours de
seconde année (rappelons que l’enseignement secondaire obligatoire comporte quatre
années). Ces extraits ont été choisis pour être mis en correspondance avec les
exemples d’extraits de sujets d’évaluations de début de Troisième année. Le
programme est constitué de cinq « blocs » : contenus communs, nombres, algèbre,
géométrie, fonctions et graphiques, statistiques et probabilités.
Nous avons choisi des extraits relatifs au bloc des nombres et au bloc de la géométrie.
Nombres
Première année
Nombres. Divisibilité des nombres naturels. Multiples et diviseurs communs à
plusieurs nombres. Applications de la divisibilité à la résolution de problèmes
associés à des situations quotidiennes. Nécessité des nombres négatifs pour exprimer
des états et des changements. Reconnaissance et conceptualisation dans des contextes
réels. Signification et utilisation des opérations avec des nombres entiers. Utilisation
de la hiérarchie et des propriétés des opérations et des règles d’utilisation des
parenthèses dans des calculs simples. Fractions et décimaux dans des environnements
quotidiens. Différentes significations et utilisations des fractions. Opérations avec les
fractions : addition, soustraction, produit et quotient. Nombres décimaux. Relations
entre fractions et décimaux. Élaboration et utilisation de stratégies personnelles pour
le calcul mental, pour le calcul approché et avec la calculatrice. Rapport et proportion.
Identification et utilisation, dans des situations de la vie quotidienne, de grandeurs
directement proportionnelles. Application à la résolution de problèmes dans lesquels
intervient la proportionnalité directe. Pourcentages pour exprimer des compositions
ou des variations. Calcul mental et écrit avec des pourcentages habituels.
Deuxième année
Nombres. Puissances de nombres entiers avec exposant naturel. Opérations sur les
puissances. Utilisation de la notation scientifique pour représenter des grands
nombres. Carrés parfaits. Racines carrées. Estimation et obtention de racines
approchées. Relations entre fractions, décimaux et pourcentages. Utilisation de ces
relations pour élaborer des stratégies de calcul pratique sur les pourcentages. De
même, utilisation pour le calcul mental, écrit ou avec calculatrice, de stratégies de
comptage ou d’estimation des quantités de manière cohérente avec la précision requise
par le résultat ou par la nature des données. Proportionnalité directe et inverse.
Analyse de tableaux. Coefficient de proportionnalité. Augmentations et diminutions
en pourcentage. Résolution de problèmes en rapport avec la vie quotidienne dans
lesquels apparaissent des relations de proportionnalité directe ou inverse.
Géométrie
Première année
Éléments de base pour la description des figures géométriques du plan. Utilisation de
la terminologie adéquate pour décrire avec précision des situations, formes, propriétés
et configurations du monde physique. Analyse des relations et des propriétés de figures
planes : parallélisme et perpendicularité. Emploi de méthodes inductives et déductives
pour analyser des relations et des propriétés dans le plan. Constructions géométriques
simples : médiatrice, bissectrice. Classification des triangles et des quadrilatères à
partir de différents critères. Étude de quelques propriétés et de relations dans ces
polygones. Polygones réguliers. Circonférence et cercle. Construction de polygones
réguliers avec les instruments de dessin habituels. Mesure et calcul d’angles dans des
figures planes. Estimation et calcul de périmètres de figures. Estimation et calcul
d’aires par des formules, la triangulation et la quadrangulation. Symétrie de figures
planes. Repérage de la symétrie dans la nature et dans les constructions. Emploi
d’outils informatiques pour construire, simuler et faire des recherches sur des relations
entre des éléments géométriques.
Deuxième année
Figures de même forme et de tailles différentes. La similitude. Proportionnalité de
segments. Identification de relations de similitude. Agrandissement et réduction de
figures. Obtention, quand ce sera possible, de l’échelle utilisée. Rapport entre les aires
de figures semblables. Utilisation des théorèmes de Thalès et de Pythagore pour
obtenir des mesures et vérifier des relations entre des figures. Polyèdres et solides de
révolution. Développements plans et éléments caractéristiques. Classification relative
à différents critères. Utilisation de propriétés, de régularités et de relations pour
résoudre des problèmes du monde physique. Volumes de solides géométriques.
Résolution de problèmes impliquant l’estimation et le calcul de longueurs, d’aires et
de volumes. Utilisation de procédures comme la composition, la décomposition,
l’intersection, la troncature, la dualité, le mouvement, la déformation ou le
développement de polyèdres pour les analyser ou en obtenir d’autres.
Références
Chevallard, Y. 2002. Organiser l’étude 3. Écologie & régulation. In : Dorier, J.-L. et
al. (éds). Actes de la 11e école de didactique des mathématiques. La Pensée Sauvage,
Grenoble.
Décret royal du 29 décembre 2006 organisant les enseignements minimaux dans
l’éducation secondaire. Téléchargeable le 26/01/08 sur :
http://www.mec.es/mecd/gabipren/documentos/files/desarrollo-loe-rdl-eso.pdf
Épreuve d’évaluation diagnostique de milieu de scolarité secondaire :
http://www.adelat.org/media/docum/prueba.pdf































