Il n’y a pas que les enfants qui changent, évoluent, se transforment du CP au lycée. Il en va des concepts mathématiques comme des élèves : eux aussi se modifient au fur et à mesure des cycles. Penchons nous sur l’un d’entre eux : le signe \(=\) et sa lente croissance. Croissance inapparente : les deux barres du signe restent sagement parallèles et de même longueur tout au long du processus, et pourtant, que d’évolutions en quelques années…

Dès le cycle 2, le signe \(=\) naissant fait ses premières timides apparitions, dans la comparaison des collections, en compagnie de deux complices qui sont \(<\) et \(>\).

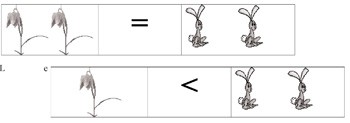
Le mathématicien peut être surpris de son emploi dans un tel cadre. Il n’y a pas de quoi se formaliser outre mesure. L’enfant apprend à identifier une propriété forte : la notion de nombre entier, propriété commune à …, et c’est bien d’une égalité qu’il s’agit en sous-sol.

Mais, au CP, le signe \(=\) prend rapidement un autre statut. Il apparaît comme l’exécuteur des œuvres opératoires, celui qui donne LE résultat d’une opération. À sa gauche, un signe opératoire (au début un seul), placé entre deux nombres. À sa droite, un nombre, LE résultat.

Notre signe égal est, dans ces âges-là, un signe orienté, qui fonctionne de gauche à droite. Il est alors très proche de sa cousine, la touche EXE de la calculatrice, qui, elle, restera incapable toute sa vie de retour en arrière.

Assez vite cependant, il va commencer à être vu comme un être légèrement symétrique, symétrique seulement dans des cadres bien précis. Au CP, dans l’indispensable étude des décompositions des premiers nombres entiers et l’apprentissage par cœur des compléments à dix.

\(10 = 1 + 9\)
\(10 = 2 + 8\)… Vous connaissez la suite.

Cet égal « dans l’autre sens » est utilisé aussi dans le travail autour de la numération de position : \(127 = (1 × 100) + (2 × 10) + 7\) et plus tard au cycle 3 dans l’extension du côté de la partie décimale : \( 3,47 = 3 + \frac{4}{10}+ \frac{7}{100}\)

Mais hormis les exemples ci-dessus, le signe égal peine, jusqu’à la fin du cycle 3, à acquérir son statut pleinement symétrique. N’oublions pas que nous sommes dans la lente construction d’une relation d’équivalence. Il me semble que, si l’on peut penser que la réflexivité s’est un peu construite autour de nos deux fleurs égalant nos deux lapins, la symétrie gagnerait à être travaillée davantage dans la scolarité primaire, à travers des exercices simples du genre égalités trouées comme :

\(12+ … = 20-3\)

La première question du Kangourou 2006 :

n’a été réussie que par 68% des élèves de sixième.

Ensuite, le signe égal rentre au collège. Là, de la sixième à la quatrième, il va subir des modifications profondes, pour parvenir au signe égal adulte, dans toute la diversité de ses statuts. Et cette croissance rapide est source de difficultés. Surtout que, bien souvent, comme pour nos enfants, on ne le voit pas grandir.

D’abord, la question de la transitivité : les signes \(=\) à la queue leu leu, vont faire leur apparition. On sait qu’ils sont un premier obstacle.

Dans un calcul à plusieurs opérations, l’élève va être tenté de mettre juste un résultat à la fin. Normal : c’est la première acception qu’il a intégré du signe égal, la touche EXE de la calculatrice, qui est prégnante. Et là, le prof n’est pas content du tout : il exige des étapes de calcul. Alors, pour lui faire plaisir, l’élève va en écrire. Comme, chez lui, la symétrie du signe égal n’est pas vraiment construite, il va écrire comme il parle.

\(4 + 5 = 9 × 3 = 27\) quand on lui demande de calculer \((4 + 5) × 3\).

Nouvelle ire du professeur. Pourtant, la faute se comprend très bien : elle vient à la fois des habitudes de l’oral et aussi de la vision d’une égalité comme un connecteur à 3 places : \(+\) \(=\).

L’enfant isole mentalement les deux morceaux, \(4 + 5 = 9\) et \(9 × 3 = 27\). Et pourquoi cela serait-il mal à l’écrit alors que c’est courant à l’oral ? Ce n’est qu’en expliquant patiemment le nouveau statut symétrique du signe égal, en pointant systématiquement dans les écritures erronées le signe \(=\) qui relie deux nombres non égaux (le premier des deux dans l’exemple ci-dessus), que l’on aidera l’élève à dépasser la construction initiale et à se fabriquer une nouvelle représentation du signe \(=\), plus conforme aux besoins du mathématicien.

Mais voilà que, fin de cinquième, début de quatrième, le signe égal commence à avoir de mauvaises fréquentations. Au lieu de ses vieux copains de toujours, ces nombres sympathiques aux têtes connues, on le rencontre maintenant entouré d’individus douteux, ces \(x\) et ces \(y\), dont on ne sait pas trop bien ce qu’ils valent.

Avec l’arrivée des variables, la situation se complique d’un cran. Le signe égal devient schizophrène : dédoublement de la personnalité. Il y a d’abord le signe égal des identités, le signe égal toujours vrai quelles que soient les valeurs de la variable : il a élargi son champ d’action en grandissant, mais il est dans la continuité du signe égal entre nombres connus. Du 2 + 3 = 5, on est d’abord passé à 9 + 3 = 6 × 2 puis à \(x\) + \(x\) = 2\(x\) ou à \((x + 1)^2 = x^2 + 2x + 1\), ces deux dernières égalités étant vraies quel que soit le nombre \(x\). Beaucoup de chemin a été parcouru, certes, mais sous forme d’enrichissements successifs, sans rupture majeure.

Ce signe \(=\) et la cohorte d’activités qu’il amène avec lui, sous le nom de calcul littéral nécessite pourtant un apprentissage attentif. La pratique des mécanismes fait oublier le sens. Les élèves oublient souvent d’écrire les signes égal en début de ligne, montrant par là que la vraie nature de l’activité leur échappe. Ce n’est pas une étourderie, une simple négligence : c’est un indice du fait que l’élève a perdu de vue qu’il est en train de travailler sur des égalités toujours vraies. C’est pour cela que, pour éradiquer les erreurs classiques du calcul littéral, il ne faut pas hésiter à revenir au sens, à la patiente substitution de valeurs numériques.

Il est plus long, mais sans doute plus efficace à terme de dire : « Tu as remplacé \(x\) \(×\) x par 2\(x\). Quand tu fais cela, tu affirmes que pour tout nombre x, les résultats des deux calculs \(x\) × \(x\) et 2\(x\) vont donner le même résultat. Essaie donc avec \(x\) = 3… » que de dire « Tu sais bien que \(x\) × \(x\) ne fait pas 2\(x\). C’est \(x\) + \(x\) qui fait 2\(x\). Tu confonds multiplication et addition ». Démasquer le quantificateur caché dans les identités en revenant fréquemment à un calcul numérique sur quelques valeurs prend du temps, mais c’est un temps nécessaire.

En même temps, à côté de ce signe égal des identités, se profile son frère beaucoup moins fiable, ce signe égal ni vrai ni faux, mais parfois vrai, parfois faux, suivant les valeurs de la variable. Le signe égal des équations. Rien ne le distingue de son frère jumeau dont il diffère pourtant fondamentalement. Ce signe égal conditionnel dont la vérité oscille constamment au gré des valeurs de la variable est une vraie nouveauté ; et seul le professeur est à même d’expliquer à l’élève le saut conceptuel qu’on lui demande d’effectuer. Pour les bons élèves, ce changement de statut, conscient ou non, ne sera pas un obstacle. Mais le plus grand nombre ne s’en tirera pas sans l’aide de l’enseignant. Et plus celui-ci sera conscient de la difficulté, plus efficace sera son aide.

Surtout que notre pratique usuelle n’aide pas à clarifier les choses.

Regardez cette honnête résolution d’équation du premier degré telle que nous l’écrivons en Troisième ou en Seconde.
\(2(x + 1)^2 -(2x^{2}- 1) = 0 \) (1)
\(2x^2 + 4x + 2- 2x^2 + 1 = 0 \) (2)
\(4x + 3 = 0\) (3)
\(4x = -3\) (4)
\(x = -3/4 \) (5)
Chacune de ces lignes comporte en son sein un signe égal. Mais il s’agit du deuxième égal, le égal de l’équation, le égal ni vrai ni faux.

Entre la ligne (1) et la ligne (2), ou entre la ligne (2) et la ligne (3) il n’y a rien d’écrit. Pourtant, il y a sous-entendu un vrai signe égal, un signe égal d’identité, qui justifie la transformation : les lignes (1), (2) et (3) disent le même chose parce que :

\(2(x + 1)^2 -(2x^2 - 1) = 2x^2 + 4x + 2 - 2x^2 + 1 = 4x + 1\)

avec ici des signes \(=\) vrais quelles que soient les valeurs de \(x\), des signes \(=\) d’identité. Mais ceux-là ne sont pas écrits, ils sont sous-entendus [1]. Mais ensuite, quand on passe de la ligne (3) à la ligne (4), toujours sans rien écrire entre les deux, cela signifie toute autre chose : on se permet de remplacer la ligne (3) par la (4) parce que les valeurs de la variable pour lesquelles le signe \(=\) est vrai à la ligne (3) sont les mêmes que celles pour lesquelles il est vrai à la ligne (4).

Quand au signe égal de la ligne (5), je me demande s’il ne serait pas lui d’une autre nature, un troisième signe égal, qui s’apparenterait au signe d’affectation des informaticiens.

Mais là, je sens que j’exagère et que vous allez refuser de me suivre plus avant jusqu’au détriplement de la personnalité du signe égal !

Reconnaissez quand même que, sous son apparente simplicité, cette résolution d’équation cache bien des pièges et sous-entendus pour un élève qui n’aurait pas appris à lire entre les lignes.

Alors, plutôt que de s’étonner devant l’échec et la perte de sens, on devrait s’extasier devant ceux de nos élèves qui parviennent à maîtriser une construction aussi complexe. Et tenter d’aider les autres, sans doute pas en leur racontant tout cela comme je viens de le faire, mais en n’oubliant pas, en parallèle avec la nécessaire pratique des mécanismes, de revenir au sens des choses, par petites touches, à l’occasion, peu à peu et souvent.

Ainsi en est-il des signes mathématiques comme des individus : à travers évolutions, ruptures, et discontinuités, émerge peu à peu leur vraie personnalité, riche et complexe. Oui, vraiment, de la sortie de la maternelle au bac, le signe égal a bien changé !

Bibliographie

• Du numérique au littéral, document d’accompagnement des programmes de collège
  (consultable sur http://eduscol.education.fr).
• Michel de Cointet et Henri Bareil, Égalités et équations
  Bulletin de l’APMEP n° 446, p. 347-354.
• Groupe d’enseignants de l’académie d’Amiens, Le calcul algébrique
  pistes pour une progressivité des apprentissages de l’école au lycée.
  Brochure éditée par l’IREM Paris 7.