Roland Charnay [1]

Le décret relatif au socle commun de connaissances et de compétences prend soin de
préciser, dans la partie relative aux principaux éléments de mathématiques que « Il
est nécessaire de créer aussi tôt que possible à l’école primaire des automatismes en
calcul, en particulier la maîtrise des quatre opérations qui permet le calcul mental ».

Cette formulation ne manque pas d’interroger le lecteur sur au moins deux points.

Premièrement, pour quelle raison les rédacteurs ont-ils éprouvé le besoin d’insérer ce
« aussitôt que possible », seule précision de ce type dans l’ensemble du texte, toutes
disciplines confondues ? Cela signifie-t-il que, dans d’autres domaines, on pourrait
ne pas entreprendre les apprentissages visés dès que c’est possible … ou même qu’on
pourrait le faire le plus tard possible ? Peut-être ont-ils simplement voulu dire que,
actuellement, on tarde trop à mettre en place certaines connaissances. Il faudrait alors
apporter des précisions argumentées qui éclairent le propos. Ou alors, cette précision
est-elle destinée à répondre à ceux qui estiment qu’il faut étudier les quatre
opérations dès le Cours Préparatoire, c’est-à-dire avec des enfants de 6-7 ans, comme
cela était fait en des temps idéalisés, pour ne pas dire « idyllisés ». Ce serait alors à
rapprocher du rapport parlementaire sur l’enseignement des disciplines scientifiques
dans le primaire et le secondaire
 [2]qui recommande de « développer le calcul mental
et l’apprentissage des techniques opératoires des quatre opérations dès le cours
préparatoire ».

Deuxièmement, la formulation finale relative à « la maîtrise des quatre opérations
qui permet le calcul mental » paraît curieuse. On pourrait, en effet, tout aussi bien
affirmer que c’est la maîtrise du calcul mental qui permet la maîtrise des quatre
opérations ou encore que le calcul mental est un élément essentiel de la maîtrise des
quatre opérations.

Ces extraits de textes sont à resituer dans le cadre des analyses, débats et
controverses qui se développent depuis quelques années autour de l’enseignement du
calcu [3] Au moment où ce texte est écrit, le ministre s’apprête, semble-t-il, à annoncer le retour à l’enseignement des quatre opérations dès l’école maternelle,
faisant fi de tous les travaux conduits depuis 50 ans en psychologie cognitive et en
didactique, et même depuis plus de 100 ans puisque les principaux inspirateurs du
ministre s’appuient « sur la synthèse des pédagogies innovantes recensées en 1887
par Ferdinand Buisson » [4] !

La présente contribution a pour objet d’apporter un point de vue développé en partant
d’une analyse des besoins en calcul de tout individu et en se fondant sur un cadre
théorique permettant de clarifier ce qu’on peut appeler « maîtrise d’un concept »,
illustré par l’exemple de l’apprentissage de la division.

Que faut-il apprendre sur les quatre opérations ?

Quelles connaissances et quelles compétences dans le domaine du calcul numérique
un élève doit-il maîtriser à l’issue de sa scolarité obligatoire et, auparavant, lorsqu’il
sort de l’école primaire ? La question paraît saugrenue à certains tant la réponse
semble aller de soi. La tradition aurait répondu depuis longtemps ! C’est ignorer que,
depuis une vingtaine d’années au moins, l’univers du calcul a connu des
bouleversements considérables qui peuvent conduire à reconsidérer les objectifs
d’apprentissage. Jusqu’aux années soixante ou soixante-dix, un enfant voyait ses
parents effectuer leurs comptes ordinaires avec un papier et un crayon et les
commerçants avaient le crayon sur l’oreille, toujours disponible pour « faire la
note ». Ils rendaient la monnaie en complétant la somme due jusqu’à la somme
donnée : Et trois qui font soixante-dix, dix qui font quatre-vingts et vingt qui font
cent. Aujourd’hui, le relevé bancaire est vérifié en utilisant une calculatrice et la
machine du commerçant affiche à la fois la somme à payer et la somme à rendre au
client. Le calcul instrumenté a très largement remplacé le calcul posé. Celui-ci était
un enjeu essentiel des apprentissages numériques pour la vie de tous les jours. Il ne
l’est plus. Que faut-il en conclure pour l’enseignement ? Poser la question n’est pas
blasphématoire, comme certains le laissent supposer. Mais, d’un autre côté, la
réponse n’est pas contenue dans la question.

La commission de réflexion sur l’enseignement des mathématiques (dite commission
Kahane [5]) indique d’ailleurs au début du rapport consacré au calcul que l’une des
raisons de l’opportunité de ce rapport « est que, dans la période récente, le
développement des technologies informatiques a profondément modifié les pratiques
associées au calcul, tant les pratiques quotidiennes et sociales que les pratiques
scientifiques. La plupart des algorithmes de calcul dont l’apprentissage occupait un
temps important de la scolarité, notamment dans l’enseignement obligatoire, sont
aujourd’hui implantés dans les calculatrices les plus simples. En revanche, le calcul
pose des questions nouvelles liées notamment à la représentation informatique des
objets mathématiques sur lesquels il porte (par exemple la représentation
informatique des nombres), à la performance des algorithmes utilisés au delà de leur
seule effectivité…, des questions qui n’étaient pas des enjeux de l’enseignement
jusqu’ici. La puissance de calcul des nouveaux outils modifie aussi profondément
l’économie du calcul et pose, dans des termes renouvelés, celle de la gestion des
rapports entre calcul et raisonnement, en favorisant explorations, simulations,
expérimentations ».

Dans l’immédiat, concernant les techniques opératoires posées, nous ferons nôtre la
proposition énoncée dans le rapport de la CREM : « Il est évident qu’aujourd’hui, le
calcul numérique exact que nous faisons à la main, sans assistance, est très limité. Il
semble difficile d’exiger de l’école qu’elle consacre un part importante du temps
réduit dont elle dispose pour développer des compétences que plus personne
n’utilise. Dans le même temps, nous souhaitons, à juste titre, que les élèves ne soient
pas dépendants de leur calculatrice pour le moindre calcul. Ceci nécessite, au delà
de la mémorisation d’un répertoire et de compétences de calcul mental, la mise en
place de techniques de calcul écrit, et une fiabilité de ce calcul dans les cas
simples ». Dans la suite, sur l’exemple de la division, seront précisés d’autres intérêts
du travail sur ces techniques et sera proposée une analyse des conditions de leur
enseignement.

Revenons à la question des connaissances indispensables en calcul. La réponse doit
bien entendu être examinée sous l’angle de ce qui sera utile, voire indispensable, à
chacun dans sa vie quotidienne, plus largement pour pouvoir agir en citoyen informé
et responsable [6]. Il faut également penser à ce qui pourra être nécessaire au plus
grand nombre pour pouvoir profiter de nouvelles formations. Au-delà, il convient de
réfléchir à ce que peuvent être les apports de l’apprentissage du calcul à la formation
personnelle de chacun, au développement de la rigueur et du raisonnement, mais
également des capacités d’initiative, de créativité [7]

Pour dire les choses rapidement, savoir calculer c’est tout à la fois [8] :

• être capable de rendre calculables des situations (issues de la vie courante
  ou d’autres disciplines…), par un travail de modélisation qui nécessite de
  retenir certaines caractéristiques de ces situations et d’en ignorer d’autres ;
• être capable de traiter des calculs, de façon automatisée ou raisonnée, pour
  aboutir à un résultat exact ou approché, l’apprentissage et la compréhension
  des algorithmes comme l’élaboration de stratégies raisonnées nécessitant une
  bonne connaissance des nombres, des opérations et de certaines de leurs
  propriétés ;
• être capable d’organiser, de « programmer » un calcul pour le rendre
  exécutable, par soi-même ou par une machine (calculatrice, tableur, …), ce
  qui suppose une certaine connaissance des potentialités et des limites des
  outils utilisés.

Sans entrer dans un détail qui nécessiterait de longs développements [9], insistons sur
quelques points.

La priorité à accorder au calcul mental doit être constamment réaffirmée. Elle est
soutenue par plusieurs arguments qui en justifient une pratique régulière :

• le calcul mental demeure un mode de calcul largement utilisé dans la vie
  quotidienne ou professionnelle : c’est un moyen rapide d’évaluation et de
  prise de décision ;
• –c’est un outil privilégié pour contrôler un résultat obtenu par d’autres
  moyens ;
• sans bonne maîtrise des tables, le calcul posé est rendu impossible ;
• il joue un rôle primordial dans l’aide à la conceptualisation ; on peut citer
  l’exemple des raisonnements relatifs au traitement de situations de
  proportionnalité qu’on apprend d’abord à mettre en oeuvre avec des « petits »
  nombres pour lesquels un calcul mental est suffisant… mais aussi nécessaire :
  comment trouver le prix de 27 objets identiques sachant qu’un paquet de 3 de
  ces objets coûte 20 € si on ne perçoit pas très rapidement que « 27, c’est 9 fois
  plus que 3 » ?
• il constitue une aide à la résolution de problèmes, lorsqu’on cherche à
  déterminer ce que pourrait être la solution avec des nombres plus simples ;
• il est une occasion privilégiée de développer initiative et raisonnement
  lorsqu’on est confronté à une question de « calcul réfléchi » : multiplier 25 par
  8 nécessite le choix d’une stratégie et un raisonnement pour la mettre en œuvre, en faisant appel à des connaissances diverses selon qu’on cherche à
  calculer 25 x 2 x 2 x 2 ou « 8 fois 20 plus 8 fois 5 » ou « 25 x 4 x 2 »…

Le travail sur le calcul posé des opérations qui, selon le rapport de l’Inspection
Générale, « apparaît le plus pratiqué » doit être justifié par autre chose que par
l’utilité pratique de ce type de calcul qui, s’il n’est pas totalement abandonné, voit
son usage très restreint. Que peut donc apporter son apprentissage ?

• Une occasion de calculer mentalement, prétendent certains ; ce n’est pas
  totalement inexact, mais ce serait utiliser une machine bien lourde alors que
  des occasions moins risquées peuvent être aisément trouvées.
• Une opportunité de confronter les élèves à l’exécution d’algorithmes, activité
  utile en mathématiques (pas seulement d’ailleurs) et nécessitant une bonne
  concentration de la pensée. L’argument mérite d’être entendu. Il ne trouvera
  pleinement sa force que si les élèves peuvent effectivement centrer leur
  attention sur l’algorithme et ne sont pas trop embarrassés par le manque de
  disponibilité des résultats élémentaires, ce qui plaide pour une mise en place
  de ces algorithmes qui ne soit pas trop précoce.
• Une occasion de travailler les propriétés des nombres et des opérations en
  axant une partie importante de l’apprentissage sur un effort de compréhension
  et de justification des étapes de ces algorithmes. C’est sans doute l’argument
  le plus décisif. Travailler sur la technique opératoire de la multiplication, c’est
  ainsi s’attacher à faire comprendre que multiplier 457 par 306 revient à
  multiplier 457 par 6 et par 300 puis à additionner les deux résultats et que
  multiplier 457 par 300 revient à multiplier 457 par 3 puis le résultat par 100…
  Sont alors à l’oeuvre des connaissances (éventuellement en actes) relatives à
  la numération décimale (décomposition de 306) et à des propriétés de la
  multiplication (distributivité sur l’addition, associativité, …). Cela suppose de
  ne pas se limiter à un apprentissage techniciste (le comment), mais de
  chercher à justifier les différentes étapes du calcul et leur articulation (le
  pourquoi), c’est-à-dire à faire des mathématiques !

La possibilité d’utiliser les calculatrices dès l’école primaire fait débat. Certains
jugent cet usage prématuré, arguant du fait qu’il serait un obstacle à l’apprentissage
du calcul, notamment du calcul mental. D’autres, comme les inspecteurs généraux
dans leur rapport déjà mentionné, estiment que, comme pour le calcul mental, une
attention suffisante doit être portée au calcul instrumenté qui « n’est l’objet d’un
apprentissage organisé que pour une très faible minorité de maîtres ». Ces machines
à calculer faisant partie de l’environnement habituel des élèves, le rôle de l’école
paraît évident : apprendre à s’en servir de manière raisonnable et raisonnée…

Penser un apprentissage sur la durée : l’exemple de la division [10]

Voila bien un apprentissage qui fait couler beaucoup d’encre. Depuis ceux qui
s’alarment de ce qu’elle ne serait plus enseignée (marquant ainsi leur réelle
méconnaissance des textes et de la réalité ou révélant leurs arrières pensées), en
passant par ceux qui regrettent qu’on ne pose de division dès le CP jusqu’à ceux qui
estiment qu’on devrait, à l’heure des calculatrices et des ordinateurs, arrêter l’usage
de la potence, symbole de la division posée.

Comment y voir plus clair sur une question dont la complexité n’est pas mince ? Est6il
possible d’envisager tôt certains aspects de la division ? Lesquels gagneraient à être
éventuellement retardés ?

Un cadre pour examiner la question de l’apprentissage de la division

La maîtrise d’un concept n’est jamais totalement aboutie. Elle résulte d’un long
processus et peut être étudiée en se référant à différents aspects du concept.
Le schéma suivant qui propose l’analyse d’un concept (ici la division) en quatre
pôles est largement inspiré de la caractérisation d’un concept proposée par Gérard
Vergnaud.

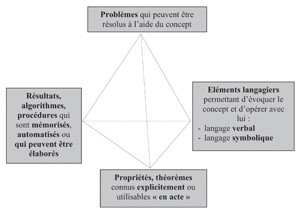
Comme le montre cette schématisation, ces quatre pôles sont évidemment en forte
interaction. Ce qu’il ne montre pas, mais qui devra être pris en considération, ce sont
les relations (plus ou moins étroites) que le concept entretient avec d’autres concepts,
par exemple la multiplication si on considère le concept de division. C’est ce qui a
conduit Gérard Vergnaud a évoquer l’idée de champ conceptuel.

Bien qu’il soit difficile d’isoler un aspect d’un concept (matérialisé par un pôle ici),
tentons pour chacun d’eux, à propos de la division d’examiner ce qui peut faire
difficulté et quelles étapes d’apprentissage peuvent être envisagées.

La difficulté des problèmes « de division »

La reconnaissance des problèmes qui peuvent être résolus à l’aide d’une division (ce
qu’on a coutume d’appeler « sens de la division ») est source de difficultés pour les
élèves, davantage que pour les trois autres opérations. Nous ne livrons ici que
quelques éléments d’analyse de ces difficultés.

À l’entrée en sixième en 2003, le problème suivant n’est résolu correctement que par
environ 55 % :

Xavier range les 50 photos de ses dernières vacances dans un classeur. Chaque page contient 6 photos.
 a) Combien y a-t-il de pages complètes ?
 b) Combien y a-t-il de photos sur la page incomplète ?

Pour être situé dans le champ de la division, la première question posée doit être
ramenée à la suivante : « Combien de fois le nombre 6 est-il contenu dans le nombre
50 ? ». Dans ce problème du type « répartition équitable », il s’agit de chercher ce
qui est traditionnellement appelé « le nombre de parts ».

Si on avait évoqué une situation dans laquelle il faut, parmi 50 photos, en placer le
plus possible sur 6 pages, avec le même nombre de photos par page, la question
« Combien doit-on placer de photos par page ? » revient à chercher ce qui est
traditionnellement appelé « la valeur de chaque part ».

La distinction entre problèmes dans lesquels il faut chercher le nombre de parts
identiques et problèmes dans lesquels il faut chercher la valeur de chaque part
identique n’est pas nouvelle. Une difficulté pour les élèves est de comprendre qu’une
même opération, la division, permet de répondre à ces deux catégories de questions.
Cette compréhension doit faire l’objet d’un travail approfondi au cycle 3 de l’école
primaire, l’une des clés résidant dans le fait que les deux catégories de questions
peuvent être résolues en cherchant le nombre qui, multiplié par 6, permet de
s’approcher le plus possible de 50, ce qui souligne les liens étroits entre division et
multiplication.

Une autre difficulté des problèmes réside dans le fait que, dans certains cas, il faut
décider de « la bonne division » à utiliser. Dans les exemples précédents, il s’agit de
la division euclidienne : il faut chercher le quotient et le reste entiers. Si la question
avait porté sur la longueur de chaque ruban obtenu en partageant une bande de 50 cm
en 6 rubans de même longueur, il aurait fallu donner une réponse sous forme
fractionnaire ou une réponse approchée sous forme décimale et la notion de reste
n’intervient alors pas.

Quand peut-on proposer des problèmes « de division » aux élèves ?

Prenant en compte les difficultés qui viennent d’être évoquées, on pourrait conclure
que de tels problèmes ne peuvent être proposés qu’assez tard, à la fin de la scolarité
primaire. Il n’en est rien. Dès que les élèves sont capables de dénombrer, ils
deviennent capables de traiter de tels problèmes.

Considérons une situation du type : un certain nombres d’images étant réparties dans
des enveloppes à raison de tant d’images par enveloppe, trouver le nombre
d’enveloppes nécessaires pour y placer le plus possible d’images (situation de type
« recherche du nombre de parts »).

Dès la fin de l’école maternelle, des questions peuvent être posées aux élèves à ce
sujet. La résolution prend appui sur un matériel, mais des conditions peuvent être
créées pour que les élèves aient un effort de réflexion, de recherche à fournir.

Donnons deux exemples.

 Exemple 1 : Les élèves disposent de 15 images. Ils savent que chaque enveloppe
devra contenir 3 images. Ils doivent commander les enveloppes nécessaires.
Ils peuvent répondre en groupant leurs images par paquets de trois, puis en comptant
les paquets obtenus, un paquet étant assimilé à une enveloppe.

 Exemple 2 : Les élèves disposent de plusieurs enveloppes et d’un crayon. Ils savent
qu’il y a 12 images dans une boîte (inaccessible pour eux) et qu’on placera 3 images
par enveloppe. Ils doivent préparer les enveloppes.

La résolution est plus délicate que dans le premier exemple. Ils peuvent, par exemple,
dessiner des images sur les enveloppes en veillant à s’arrêter dès que 12 images
auront été dessinées.

Les mêmes types de questions peuvent être posées au cours des années suivantes,
mais avec d’autres conditions : nombres plus grands, pas de matériel mis à
disposition, …

À la fin du CP ou au CE1, les problèmes peuvent être résolus en ayant recours à
l’addition itérée. Un peu plus tard, la soustraction peut également être utilisée, puis
le recours à des essais multiplicatifs devient possible.

Ce n’est qu’au cycle 3 que la division sera instituée comme moyen efficace de
résoudre rapidement cette catégorie de problèmes. Mais, à ce moment là, les
situations de référence seront devenues familières aux élèves (s’il y a 255 images et
3 images par pages, l’interprétation sous la forme « combien de fois 3 dans 255 ? »
sera plus aisée) et la division pourra être reliée à un réseau de procédures (addition
ou soustraction itérée, encadrement par des multiples successifs, …) qu’elle
remplace avantageusement. Bref, de quoi aider à donner du sens.

Autrement dit, du point de vue de la résolution de problèmes, à la question « peut-on
enseigner tôt la division ? », la réponse est oui s’il s’agit de proposer dès l’école
maternelle des situations dites « de division » et la réponse est non s’il s’agit
d’attendre que, dès le départ, la division soit utilisée pour les résoudre. D’ailleurs, la
question pertinente ne serait-elle pas : « Comment enseigner efficacement la division
pour que les élèves en construisent plus sûrement le sens ? ».

Des résultats et des techniques qui vont s’élaborer dans la durée

La technique posée de la division qui était traditionnellement enseignée en France,
sans écriture de produits partiels ni pose de soustractions intermédiaires est d’une
grande complexité. Il suffit de se demander ce que serait le programme à élaborer
pour un automate chargé d’une telle tâche pour s’en rendre compte. Une brochure de
l’APMEP consacrée à l’enseignement de la division [11] propose ainsi un
ordinogramme de calcul qui tient sur deux pages entières et ne comporte pas moins
de 11 variables. Et encore, ne se soucie-t-on pas de savoir si l’automate maîtrise bien
tous les résultats élémentaires nécessaires. Son auteur l’accompagne d’un
commentaire qui tient en un seul mot : « Effrayant ! ». On ne saurait mieux souligner
qu’un élève qui apprend mécaniquement cette technique, sans compréhension, court
tous les risques de se tromper ou d’être contraint d’abandonner. Avis aux amateurs
de cette technique et de son enseignement dès le CP…

Pourtant, l’apprentissage d’une technique raisonnable (c’est-à-dire en s’autorisant
l’écriture de quelques produits partiels et des soustractions intermédiaires) peut être
fructueux pour la connaissance de la division, dans la mesure où cette technique met
notamment en jeu les relations entre division, multiplication et soustraction. Cela ne
peut être exploité que si l’apprentissage de la technique est accompagné d’un travail
sur la compréhension des étapes du calcul et de leur organisation. Ce travail n’est lui-même
possible que si les résultats élémentaires sont parfaitement disponibles, ce qui
suppose une maîtrise « flexible » des tables de multiplication : il ne suffit pas de
savoir que « 8 fois 6 égale 48 », il faut pouvoir en déduire immédiatement que dans
« dans 50, il y a 8 fois 6 ». Autant dire que cet apprentissage ne peut guère être
envisagé avant la fin du CE2 ou au CM1 et qu’un travail à son sujet est encore
possible (et nécessaire) au collège.

Mais bien d’autres résultats sont à apprendre plus précocement. Dès le CP, des
doubles et des moitiés de nombres simples peuvent être mémorisés. Dès le CE1, la
réponse à des questions du type « Combien de fois 2 dans 14 ? » ou « combien de
fois 5 dans 35 ? » doit devenir rapide, en même temps que sont mémorisés les
résultats des tables de multiplication par 2 et par 5. À partir du CE2, cette
compétence doit être étendue aux autres tables de multiplication et des stratégies de
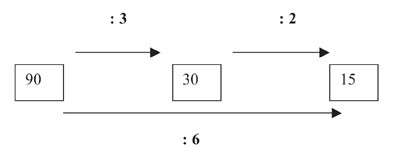
calcul réfléchi peuvent être mises en place. Par exemple, pour trouver le quotient de
la division de 90 par 6, les élèves doivent pouvoir choisir entre la procédure
consistant à diviser successivement par 3 puis par 2 ou celle qui s’appuie sur la
décomposition de 90 en 60 + 30 ou encore celle qui consiste à se demander quel
nombre doit être multiplié par 6 pour obtenir 90…

Là encore, on peut commencer tôt les apprentissages relatifs à la division sans
débuter prématurément celui qui est le plus délicat et nécessite de nombreuses autres
connaissances, c’est-à-dire celui de la division posée !

Un appui nécessaire sur les propriétés de la division

Le choix et la gestion de procédures de calcul réfléchi tout comme la compréhension
et le contrôle des étapes du calcul d’une division posée ne sont possibles que si
l’élève est capable de mobiliser, en acte ou explicitement, certaines propriétés de la
division. On en a vu quelques exemples dans le calcul du quotient de 90 par 6. On
est alors dans le cas d’une division dite « exacte », les propriétés peuvent être plus
complexes dans le cas d’une division euclidienne à reste non nul :
 la première procédure proposée suppose d’avoir compris que diviser par un
produit revient à diviser successivement par chacun des facteurs du produit ;
 la seconde nécessite de maîtriser le fait que le quotient d’une somme par un
nombre est égal à la somme des quotients de chacun des termes de la somme
par ce nombre ;
 la troisième suppose de connaître la relation entre division et multiplication.

On pourrait également citer la connaissance de l’égalité caractéristique de la division
euclidienne (a = bq + r avec \(0 \leq r< b)\) qui permet notamment de vérifier un résultat,
mais peut également être utilisée pour trouver un quotient et un reste. C’est la même
propriété qui permet aux élèves d’utiliser une calculatrice ordinaire pour obtenir un
quotient et un reste entier… Ce qui montre également que, si la calculatrice est un
outil de calcul efficace, elle peut aussi devenir un support de questions intéressantes.

Alors que cette dernière propriété est explicitée et formalisée dès que la division
euclidienne est installée au cycle 3, les autres peuvent demeurer utilisées « en acte »,
en faisant l’objet d’explicitations orales, puis codées, par exemple, pour la première,
sous la forme :

La question posée aux enseignants est de savoir à quel moment une propriété peut
être utilisée, à quel moment elle peut être explicitée verbalement, à quel moment elle
peut faire l’objet d’un codage sur des exemples (et quels codages sont possibles et
utiles à la compréhension) et à quel moment elle gagne à être généralisée en utilisant
le langage littéral. La réponse dépend à la fois, pour chaque propriété, de la
compréhension possible que peuvent en avoir les élèves, de l’usage qu’ils peuvent en
faire et des outils langagiers dont ils disposent.

Différents langages pour « parler » la division

Pour évoquer la division et les traitements à son propos, différents éléments
langagiers peuvent être utilisés.

Le langage verbal permet de décrire efficacement certaines procédures utilisées, par
exemple : « Pour diviser 90 par 6, j’ai d’abord divisé 90 par 3 puis j’ai divisé le
résultat obtenu par 2 ». Le mot « diviser » est alors le seul terme spécifique utilisé.
Dans le même registre, on pourrait expliquer que « Pour trouver le quotient de 90
par 6, on cherche d’abord le quotient de 90 par 3, puis le quotient par 2 du premier
quotient obtenu ». Un autre terme est utilisé et on perçoit aisément que cette seconde formulation sera plus difficile à manipuler que la première, notamment parce que
l’énoncé porte sur les résultats (quotient) plutôt que sur l’opération (diviser). Il y a
donc les termes à connaître (division, quotient, reste, dividende, diviseur) et il y a
aussi les formulations possibles à l’aide de ces termes qui sont d’une plus ou moins
grande complexité. Là encore, l’enseignant devra être attentif dans la progression
utilisée de façon à ne pas noyer les élèves dans cette complexité en exigeant trop tôt
des formulations dont la compréhension ne serait pas assurée.

Du côté du langage symbolique, la question est encore plus complexe.
Dans le
schéma précédent, le signe «  : » est utilisé, sans difficulté. C’est qu’on s’est placé
dans un cas simple, celui où le reste est nul, donc celui où le quotient euclidien est
égal au quotient décimal. Pour la division euclidienne, la difficulté vient du fait qu’on
a affaire à une opération à deux résultats (le quotient et le reste) ou à deux opérations
(l’opération « quotient » qui, à deux naturels, associe le quotient euclidien du premier
par le second et l’opération « reste » qui leur associe le reste). Les élèves (et les
maîtres) sont confrontés pour la première fois à cette situation qui, jusqu’à présent,
du point de vue des notations symboliques, n’a pas trouvé de bonne solution. Une
écriture du type 47 : 5 = 9 reste 2 est évidemment inacceptable, ne respectant pas les
propriétés du signe =.
On pourrait penser à une notation pour le quotient (du type :
47 q 5 = 9) et une autre pour le reste (du type 47 r 5 = 2). Elles sont également
d’usage délicat, ne mettent pas en évidence la relation entre quotient et reste et
n’étant pas, ensuite, utilisées de façon durable.

Cette question, ancienne, doit sans doute continuer à être explorée pour parvenir à
une solution consensuelle. Dans l’immédiat, il semble raisonnable d’utiliser assez tôt
le langage verbal, de privilégier l’égalité fondamentale de la division euclidienne
pour rendre compte du quotient et du reste et de réserver la notation «  : » au cas où
la division « tombe juste » ou à celui où on cherche une valeur décimale approchée
du quotient (7 : 3 » 2,33, par exemple).

Conclusion

Cette étude rapide, trop rapide, de la question de l’apprentissage de la division ne se
résoudra pas facilement, comme certains le prétendent, en avançant le moment où les
élèves apprennent le symbolisme de cette opération et sont confrontés à la division
posée à l’aide d’une potence. Elle vise, au contraire, à souligner la complexité de cet
apprentissage et à esquisser des étapes possibles pour son étude en prenant en compte
les différents aspects du concept.

Alors, quelle réponse à la question : faut-il enseigner tôt la division ?

Oui, s’il s’agit de permettre aux élèves de résoudre, à l’aide de leurs connaissances
disponibles, des problèmes dits « de division ».

Non, s’il s’agit de les mettre en difficulté en les confrontant trop précocement à ce
que la division comporte de plus délicat et de plus complexe.