480
La règle à calcul à travers les classes
L’APMEP promeut les mathématiques de la maternelle à l’université. Je jongle pour
ma part cette année, de la sixième à la terminale. Ce n’est pas de tout repos mais fort
intéressant et enrichissant.
Le manque d’élèves pour mettre les sommes algébriques en théâtre en cinquième, allié
à la question du parachutage des logarithmes en terminale m’ont curieusement poussé
à envisager une réponse analogue : la règle à calcul [1]. L’instrument n’est certes pas
nouveau mais mérite d’être manipulé voire créé.
1. Règle à additionner et soustraire les entiers relatifs (en Cinquième)
Il s’agit tout simplement de faire coulisser une règle graduée le long d’une autre
(graduation régulière, au sens habituel).
-
- Avec les nombres « habituels » [2]. : les entiers naturels
Pour additionner
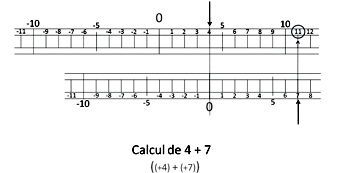
Il faut lire le premier nombre sur la règle du haut ; amener le zéro du bas sous ce
premier nombre ; lire le second nombre sur la règle du bas. Le résultat est situé juste
au-dessus de ce second nombre.
Ci-dessous, une règle fabriquée avec une feuille de papier. On plie les deux bandes
pour les faire coulisser l’une le long de l’autre et on fait la graduation des deux en
même temps.

Pour soustraire
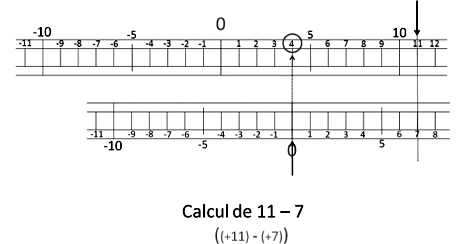
Il faut lire le premier nombre sur la règle du haut ; amener le second nombre sous ce
premier nombre. Le résultat est situé juste au-dessus du zéro du bas.
-
- Avec les nombres relatifs
Rien ne change pour la manipulation de la règle !
Une autre façon de concevoir 11 − 7
- Avec les nombres relatifs

-
-
- Et si on ajoute un négatif qui fait repasser de l’autre côté du zéro du haut
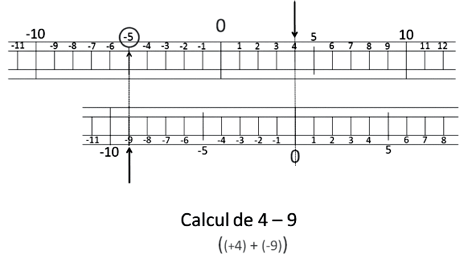
- Et si on ajoute un négatif qui fait repasser de l’autre côté du zéro du haut
-
c’est comme si on avait retiré plus que ce que l’on a !

-
-
- Ajouter deux nombres négatifs…

- Ajouter deux nombres négatifs…
-
-
-
- ou
c’est s’éloigner à gauche de zéro deux fois de suite.
Il ne reste plus qu’à retirer un négatif…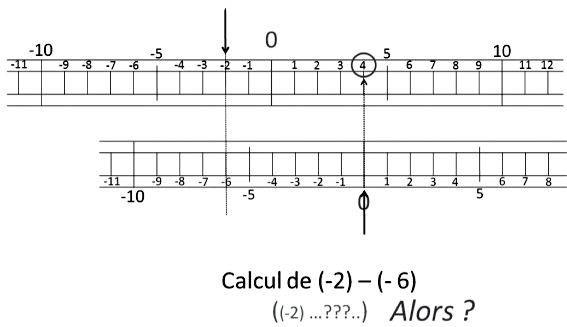
- ou
-
2. Vers une règle à multiplier (en troisième)
Il s’agit toujours de faire coulisser une règle graduée le long d’une autre, le problème
étant d’établir la graduation adéquate.
• Pour commencer
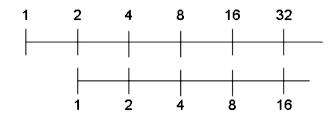
Les puissances de 2 sont celles qui permettent de placer le plus de nombres des tables
de multiplications habituelles, mais bon, ça ne fait que les puissances de 2 ; ce n’est
pas top. Pourtant si on essaye de graduer davantage…
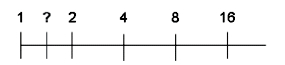
Non, non, ce n’est pas 1,5 ! En effet

il faut T × T =2 (c’est quand même bien commode l’écriture littérale). On reconnaît
(ou on définit) \(\sqrt{2}\).
Et ensuite
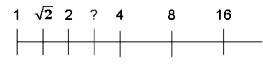
Alors, ce n’est pas 3 et non, non, ce n’est pas \(\sqrt{4}\) puisque \(\sqrt{4}=2\). C’est le nombre
qui, multiplié par \(\sqrt{2}\), donnera 4.

Hum… Mais c’est aussi …
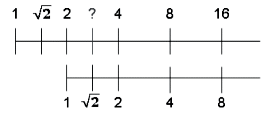
Tonnerre, \( 2\sqrt{2}\) !!! Du déplacement initial [3],

nous en sommes maintenant à
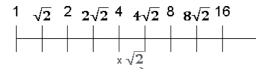
Voila donc du calcul en prévision.
D’autant que la règle à multiplier peut bien évidemment servir de règle à diviser.

ou

Voilà donc une nouvelle perspective… Barre à gauche, toute !
Et si on divisait par plus grand que le nombre de départ ?

À ce stade, si on n’a pas trop perdu les élèves, on peut espérer ne pas entendre 0 mais
bien 1/2 ; l’explication la plus convaincante étant certainement :

Ainsi, par prolongement pour
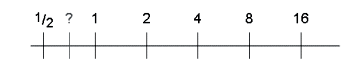
on obtient

et les différentes lectures de la position

amènent les égalités \( \frac{1}{\sqrt{2}} x 2 = \frac{2}{\sqrt{2}}={\sqrt{2} \) et\( \frac{\sqrt{2}} {2} = \frac{1}{\sqrt{2}}\) . Etc.
3. Un prolongement possible au lycée
• Où donc est 3 ? [4] .
Si les élèves de troisième ont vu l’approche avec\(\sqrt{2}\) , on peut alors envisager au
lycée de prolonger l’activité en demandant de placer 3...
Une recherche sur tableur permet d’approcher 3 par dichotomie. On obtient

ou soit encore \(2x2^{\frac{1}{2}}x2^{\frac{1}{16}}x 2^{\frac{1}{64}}x 2^{\frac{1}{128}} \)
On peut ensuite placer tous les \(2^{n} × 3^{p}\) en utilisant la règle.
• Pour conclure
Arrivé à ce stade il est temps de dévoiler les logarithmes qui permettent d’abréger
grandement les placements de 5, 7, 11, 13 et tous ces curieux nombres entiers qu’on
n’arrive pas à écrire sous forme de multiplication pour pouvoir les placer sur la
règle [5]
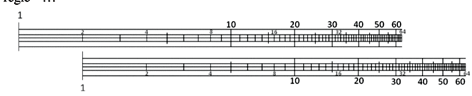
Utilisation de la règle à calculer :
En sixième : multiplication et division des décimaux, ordres de grandeurs, …
En Terminale : pour dévoiler les logarithmes ou s’en servir, selon.































