par Jacques Lucet [1]

Préambule

Soit les points distincts \(A\), \(B\), \(C\) et \(D\) de l’espace \(\mathbb R^3\). Soit aussi les réels \(\lambda\) et \(\mu\) non nuls et différents de 1.

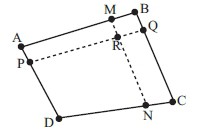
Posons M = (\(A(\lambda\)),\(B(1 - \lambda\)))
c’est-à-dire que le point \(M\) est le barycentre des points \(A\) et \(B\) affectés respectivement des coefficients \(\lambda\) et \(1 − \lambda\).

Posons encore :
\(N\) = (\(C(1 − \lambda\)),\(D(\lambda\)))
\(P\) = (\(A(\mu\)),\(D(1 − \mu\)))
\(Q\) = (\(B(\mu\)),\(C(1 − \mu\)))
\(R\) = (\(M(\mu\)),\(N(1 − \mu\))).

• Montrer que l’on a \(R\) = (\(P(\lambda\)),\(Q(1 − \lambda\))) en utilisant le théorème d’associativité
• En déduire que les droites \((MN)\) et \((PQ)\) sont concourantes.

Condition nécessaire et suffisante pour qu’un point appartienne à la surface \(S\) d’équation \(z = xy\)

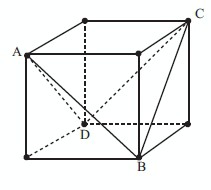
Soit les points \(A\)(1,1,1), \(B\)(−1,1,-1), \(C\)(−1,−1,1) et \(D\)(1,−1,−1) dans un repère orthonormé \((O,x,y,z)\) : ce sont quatre sommets d’un cube comme représenté ci-contre.

• Vérifier que les points \(A\), \(B\), \(C\) et \(D\) appartiennent à la surface \(S\) d’équation \(z = xy\).

• Vérifier également que les points \(M\), \(N\), \(P\) et \(Q\) définis dans le préambule appartiennent aussi à la surface \(S\) quels que soient les réels \(\lambda\) et \(\mu\).

• En déduire que les quatre droites \((AB)\), \((AD)\), \((CD)\) et \((CB)\) sont tout entières contenues dans la surface \(S\).

• Prouver enfin que le point \(R\) appartient à la surface \(S\) ; que dire des droites \((MN)\) et \((PQ)\) ?

• Réciproquement, montrer que tout point \(R\) de la surface \(S\) se trouve sur deux droites \((MN)\) et \((PQ)\) s’appuyant sur les côtés du quadrilatère \(ABCD\) et entièrement contenues dans la surface \(S\).

La surface \(S\) est donc l’ensemble des points \(R\), intersection chacun de deux droites \((MN)\) et \((PQ)\) telles que décrites précédemment. On dit que la surface \(S\) est engendrée par de telles droites. L’utilitaire Excel va nous permettre d’en visualiser quelques unes formant un maillage.

Représentation d’une portion de la surface \(S\)

Dans un tableur, indiquer en première ligne à partir de la cellule B1, puis en première colonne à partir de la cellule A2, les réels de \(−1\) à \(1\) avec un pas de \(0,1\).

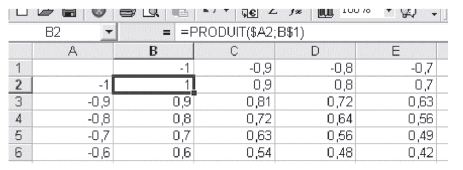
• Dans la cellule B2, recopier la formule indiquée établissant le produit des cellules A2 et B1 et étendre cette formule avec la souris jusqu’à V2, puis V22.

• Cliquer sur l’icône de l’assistant graphique et choisir « Surface » de manière à obtenir le dessin ci-dessous.

  

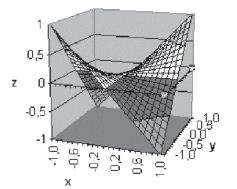
• Faire tourner la surface en cliquant sur l’un des sommets du cube et en laissant enfoncé le bouton gauche de la souris.

Intersection de la surface \(S\) avec des plans particuliers

Si l’on pose \(z = f (x,y) = xy\),

• Comparer \(f(x,y)\) et \(f(-x,-y)\)
• En déduire une propriété géométrique de la surface \(S\).
• Quelle est l’intersection de la surface \(S\) avec le plan \((xOy)\) ? Montrer que l’intersection de la surface \(S\) avec un plan parallèle au plan \((xOy)\) et différent du plan \((xOy)\) est une hyperbole.
• Montrer que l’intersection de la surface \(S\) avec un plan parallèle au plan \((zOy)\) ou au plan \((zOx)\) est une droite.
• Montrer enfin que l’intersection de la surface \(S\) avec le plan d’équation \( x − y = 0\) est une parabole.

On dit que la surface \(S\) est un paraboloïde hyperbolique.