Une activité en classe terminale STG : La droite de régression linéaire. [1]

Hervé Milliard [2]

1. Introduction

Dans le cadre des nouveaux programmes de la série STG, nous avons voulu mettre
en place une activité qui réponde à de multiples critères :
 Se conformer aux objectifs généraux de la série,
 Traiter d’un point précis et important du programme,
 Rendre accessible aux élèves de cette série une notion théoriquement difficile
à leur niveau,
 Mobiliser des capacités de lecture, d’observation, d’expérimentation,
d’analyse et de synthèse,
 Apporter une petite contribution d’histoire des maths,
 Montrer la force des nouvelles technologies pour réaliser ce pari difficile et
l’économie de temps qu’elles permettent, la possibilité de reprendre, de tester
des cas différents, d’agir en modifiant un seul facteur ou plusieurs
simultanément etc.

2. Les objectifs généraux de la série (programme de la série STG. 2005)

Les objectifs suivants sont prioritairement visés :
 entraîner à la lecture active de l’information, à sa critique, à son traitement, en
particulier en privilégiant les connaissances et les méthodes permettant des
changements de registre (graphique, numérique, algébrique, …) ;
 former les élèves à l’activité scientifique par l’acquisition de méthodes
d’observation, d’analyse critique et de déduction ;
 développer les capacités de communication écrite et orale ;
 promouvoir la cohérence de la formation des élèves en utilisant les liens entre les
différentes parties du programme et en tissant les relations entre les mathématiques
et les autres disciplines.

3. Le programme (extraits du programme concernant le thème)

Le programme de statistique est un terrain pour des activités interdisciplinaires et
pour la consolidation des techniques élémentaires de calcul : usage des fractions,
des pourcentages, proportionnalité. Les statistiques à deux variables sont
indispensables en économie et en gestion pour analyser, interpréter et prévoir.

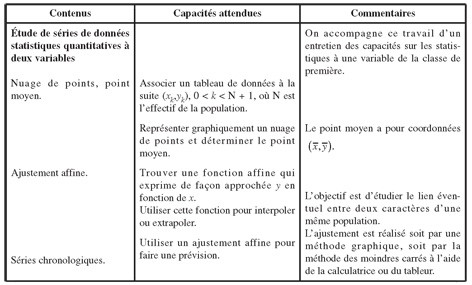
4. Les commentaires du programme (doc. Accompagnement. p. 17)

En terminale, sont introduites les séries de données statistiques à deux variables.
L’objectif est d’étudier le lien éventuel entre deux caractères d’une même population.
Pour deux variables quantitatives, on peut rechercher une formule approchée
exprimant l’une des variables en fonction de l’autre : c’est la problématique de
l’ajustement.

En première approximation, l’ajustement affine peut être réalisé graphiquement ; il
s’agit alors de tracer, « à la main », quand la forme du nuage de points s’y prête, une
droite passant « au plus près » des points du nuage.
Si l’objectif fixé par le problème le justifie, la calculatrice ou le tableur permettent
un ajustement par la méthode des moindres carrés. On peut néanmoins en expliquer
le principe :
Pour une droite donnée d’équation y = ax + b, on compare les \(y_i\) observés aux \(y_i\)
calculés (autrement dit les \(ax_i + b\)) en calculant les résidus \(y_i - (ax_i + b\)). On souhaite
trouver une droite pour laquelle ces résidus soient les plus faibles possibles. La
droite des moindres carrés, ou droite de régression, est celle qui minimise la somme
des carrés de ces résidus.

Pour un nuage donné, il est intéressant de comparer, à l’aide du tableur, la somme
des carrés des résidus pour plusieurs droites obtenues par différentes façons
(graphiquement, calculatrice, tableur) ; on vérifie, à cette occasion, que la droite de
régression fournie par le tableur, donne une somme des carrés des résidus plus faible
que les autres.

On veillera à ne traiter que des problèmes où l’ajustement affine a un sens (forme du
nuage de points presque rectiligne).

On pourra traiter un ou deux exemples de situations concrètes où les deux
ajustements ont un sens et permettent de mettre en évidence la non-symétrie du rôle
joué par chacune des deux variables.

Le professeur peut faire remarquer aux élèves que la droite de régression de y en x
n’est pas la même que celle de x en y, que ces deux droites ne sont donc pas
interchangeables (sauf dans le cas extrême où les points sont alignés) et veiller à ne
pas demander une estimation de x en y en utilisant la droite de régression de y en x.

5. Les objectifs de la séance

La trame de l’activité proposée – qui peut se faire en demi groupe en salle
informatique ou en classe entière avec un vidéoprojecteur – après avoir présenté avec
soin la problématique, reprend l’idée de la démonstration théorique de la droite de
régression. On montre d’abord qu’à coefficient directeur constant, la somme des
carrés des résidus \(S_x\) est minimale lorsque la droite passe par le point moyen, puis
que, de toutes les droites passant par le point moyen, il y en une seule qui
minimise \(S_x\) .
Lorsque cette notion est acquise, on reprend l’étude de manière analogue de la droite
qui minimise \(S_y\) et on permettra enfin aux élèves de « jouer » avec ces connaissances
en modifiant à volonté les nuages de points pour observer les variations sur \(S_x\) , \(S_y\), et
les droites d’ajustement.

L’objectif est finalement de faire comprendre ce qu’est la droite de régression, et le
fait qu’elle est unique (existence et unicité) et non d’insister sur le calcul des
coefficients de cette droite.

On pourra dire en fin de séance que l’expression y = ax + b est donnée par la
calculatrice avec une excellente précision, suffisante pour la plupart des applications
et la donner sous forme \( y=a(x-\overline x)+\overline y\).
Privilégiant là une démarche scientifique relativement autonome, une grande liberté
est donnée aux élèves pour effectuer leur recherche, faire des essais
complémentaires, rédiger les conclusions de chaque partie.

Le professeur est présent et prêt à répondre à toutes les questions et toutes les petites
angoisses. Il fera notamment la distinction entre l’exact et l’approché tout au long de
la séance.

Cette activité, faut-il le préciser, se fait après le cours sur les séries statistiques
doubles.

Cette séance sera de toutes façons suivie de bien d’autres qui permettront de montrer
tout l’intérêt de cette droite pour attribuer des valeurs de séries, pour effectuer des
prévisions, etc.

Compte rendu de séance :

La séance a lieu en une heure 15 min en salle informatique avec deux élèves par
poste. Les élèves disposent des fiches et des fichiers Géoplan sur l’ordinateur, sans
document papier.

Ils ont déjà utilisé le logiciel trois fois, ce qui leur a donné un peu de pratique et
permis de commencer à travailler l’activité dès le début. Le professeur a comme
ligne de conduite d’intervenir le moins possible, la fiche étant très détaillée.
Ce choix de détail a été délibérément fait pour éviter des questions récurrentes
d’ordre pratique et permettre une réelle activité d’enseignement et de recherche en se
concentrant sur les deux questions suivantes :
 Peut-on donner un sens précis en définissant un réel qui indique si une droite
passe « plus ou moins près » des points du nuage.
 Existe-t-il alors une droite meilleure que toutes les autres au sens défini ?
On pourra en annexe comparer les droites d’ajustement de y en x et de x en y et
observer la variation de ces droites lorsqu’on déplace des points ou que l’on en
rajoute.

Cette activité de la partie A répond au programme officiel :
« En première approximation, l’ajustement affine peut être réalisé graphiquement ;
il s’agit alors de tracer “ à la main ”, quand la forme du nuage de points s’y prête,
une droite passant “ au plus près ” des points du nuage. »
Il est enfin utile de rappeler que cette étude reprend graphiquement l’esprit de la
démonstration qui mène à la détermination de la droite de régression.

Partie A

Les élèves ont dû prendre un peu de temps pour comprendre la problématique et
prendre en main le fichier. Ils ont tout de suite compris que G représente le point
moyen et qu’il est donc logique qu’il se déplace avec les points du nuage.

La somme \(S_x\) et surtout son expression ont suscité plusieurs questions. Le professeur
a dû faire préciser au tableau avec un graphique ce qu’elle mesure précisément.

Les élèves, au final de cette partie, trouvent des résultats sensiblement différents, le
fait de jouer sur les deux variables (direction, ordonnée à l’origine) ne leur ayant pas
toujours permis de déterminer la droite de régression (bien qu’assez proche).

Ceci n’est pas gênant (au contraire !) car l’essentiel de cette partie était de
comprendre que l’on peut créer un nombre positif qui mesure la « distance de la
droite au nuage ».

La méthode qui a remporté le plus vif succès est une méthode purement graphique,
en déplaçant la droite jusqu’à ce que sa position par rapport au nuage soit
« satisfaisante » pour l’œil.

Partie B

Les élèves découvrent très rapidement que la droite qui minimise \(S_x\) passe par G, un
deuxième essai avec un nuage très différent confirmant immédiatement leur
conjecture.
J’ai pu constater une nouvelle fois la faculté chaque année meilleure des élèves de
s’adapter rapidement à l’outil informatique.

Partie C
Si les élèves n’ont eu aucune difficulté avec la détermination de la droite de
régression, ils ont eu plus de mal à comprendre l’abscisse du point \(Z_2\) dans le
repère \(R_2\) :
Le point \(Z_2\) dans le repère \(R_1\) situé à droite a pour abscisse la valeur absolue du
coefficient directeur de D et pour ordonnée la valeur de \(S_x\). Ceci a été l’occasion de
plusieurs rappels sur la représentation graphique, la valeur absolue, le coefficient
directeur d’une droite et son rôle graphique.

La première conclusion (en fait l’essentiel de la recherche) a mené globalement à des
réponses correctes, parfois inexactes ou incomplètes : « la droite idéale est la droite
qui passe par G » ; « Il y a deux droites qui minimisent \(S_x\) : l’une qui passe par G,
l’autre de coefficient directeur donné »

Partie D

À l’aide des repères \(R_2\) et \(R_3\), les élèves ont rapidement compris que ce ne sont pas
les mêmes droites qui minimisent \(S_x\) et \(S_y\). Certains ont modifié spontanément les
points du nuage pour observer l’effet sur les droites de régression.

Ceci a permis à la plupart de comprendre que c’est en alignant les points que l’on
rend confondues ces droites.

On est très proche des consignes du programme :
Le professeur peut faire remarquer aux élèves que la droite de régression de y en x
n’est pas la même que celle de x en y, que ces deux droites ne sont donc pas
interchangeables (sauf dans le cas extrême où les points sont alignés) et veiller à ne
pas demander une estimation de x en y en utilisant la droite de régression de y en x.
Dans ce cas, ce sont les élèves eux-mêmes qui ont pu faire ces observations.

Partie E

Cette partie est beaucoup plus ouverte. Elle laisse les élèves manipuler sans but
précis affiché si ce n’est d’observer comment « bouge » la droite lorsqu’on déplace
les points du nuage, soit près de G, ou au contraire éloignés, parallèlement à D ou
pas, sur la droite elle-même…

L’intérêt pédagogique est multiple : placer l’élève en situation de recherche pour
dégager tout ce qui peut apporter des résultats intéressants, voir par exemple
qu’introduire un nouveau résultat dont le point correspondant est sur D ne modifie
pas une prévision.

Quelques extraits :
« La droite varie beaucoup lorsqu’on déplace un seul point loin de D »
« Pas de changement si on bouge un point sur la droite »
« Si on rajoute un point très éloigné, la droite change parce que G change »
« Quand on rajoute un point au nuage, mais sur D, la droite ne change pas »

L’activité s’est achevée en une heure quinze, en prenant tout le temps nécessaire.
Le professeur a eu soin de demander, pour chaque partie, plusieurs réponses
écrites d’élèves et de faire une mise en commun qui permette d’établir au final
la solution correcte.
Le résumé de cette étude destiné au cours est établi au cours de l’heure suivante.

En conclusion

La démonstration qui mène à la droite d’ajustement n’est pas au programme des
séries STG ou ES, mais ici les nouvelles technologies vont permettre d’en reprendre
l’idée en montrant graphiquement dans un premier temps que, à coefficient directeur
fixé, la somme des carrés des résidus est minimale lorsque la droite passe par le point
moyen, puis dans un deuxième temps que, pour toutes les droites qui passent par G,
\(S_x\) est minimale lorsque la droite a un coefficient directeur bien déterminé.

Le professeur pourra demander aux élèves d’utiliser le logiciel pour montrer,
questionner, faire conjecturer et faire confirmer par plusieurs essais avant de
formaliser.