par Nicolas Bernard

Nicolas Bernard
enseigne dans un
collège à Redon (35)

Motivations

De nombreuses motivations différentes peuvent participer au choix de notre première heure de cours. Avec le recul, je crois que c’est avant tout la volonté d’entretenir l’enthousiasme des élèves qui m’a amené à choisir cette activité pour ma première séance en classe de 6ème.

À ce niveau, à cet âge, nous avons encore la chance de connaître un a priori souvent favorable de la part des élèves, la chance de voir de si nombreuses mains se lever à la moindre question.
Par ailleurs, mes lectures, le hasard des rencontres et ma courte expérience, me conduisent à croire de plus en plus que le plaisir d’apprendre et la curiosité sont le moteur le plus puissant d’un apprentissage de qualité.
Cette première heure a donc pour vocation de dire aux élèves, dès le début : «  On peut prendre du plaisir à faire des mathématiques  », ou pour le dire avec leurs mots à eux : « On peut s’amuser en mathématiques  ».

Lancement de l’activité

Cette première séance réclame une certaine gymnastique, aussi bien physique puisqu’il s’agira de circuler assez rapidement dans la classe, qu’intellectuelle puisque les élèves vont se retrouver confrontés à des écueils différents.
Pour ce qui est du lancement de l’activité, il est fort simple : « Prenez votre cahier de brouillon et dessinez l’armoire.  ». Des élèves accueilleront la consigne avec un certain scepticisme. Cependant, à ce que j’ai pu en voir (5 classes au total sur deux années), ils se lancent volontiers dans l’activité. Et là commence la gymnastique.
Petite parenthèse avant d’aborder les différentes réorientations des élèves durant l’activité.
À chacun ses méthodes, variables selon les contextes. Me concernant, pour cette activité, je guette tous les points à retravailler à partir des productions des élèves. Quand j’en remarque un, je réoriente l’élève personnellement, puis je m’adresse à toute la classe, sans interrompre les élèves dans leurs dessins. Ensuite, je fais rapidement le tour de la classe pour vérifier que les autres élèves concernés ont pris note de ma remarque. Tout cela en tâchant autant que possible d’encourager les élèves, toujours guidé par l’ambition d’apprendre avec plaisir, voire dans la joie et la bonne humeur. Évidemment la méthode est modulable selon la personnalité de chacun, professeur et élèves.
Cette parenthèse étant refermée, voici un petit recueil des productions rencontrées, ce qui permet d’orienter le travail des élèves.

Réorientation du travail des élèves durant l’activité

.

 Réorientation 1 : armoire dessinée de face.

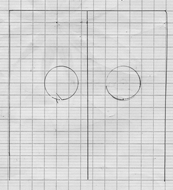
Certains élèves dessinent l’armoire de face. Même s’ils le font parfois avec une grande application, ce n’est pas le but pour moi de cette activité. Il s’agit donc simplement de leur dire qu’on veut un dessin qui fasse apparaître « le volume » de l’armoire. Il n’est pas rare que les élèves proposent l’expression « en 3D  » dont l’usage peut donc être bénéfique pour nous. On peut aussi préciser, en y ajoutant une gestuelle convaincante, qu’on veut voir sur leur dessin qu’ils ne sont pas en train de dessiner un objet plat. Il n’est généralement pas compliqué de les réorienter sur ce point.
 

 

 

 

 Réorientation 2 : point de fuite et perspective cavalière.
 

 

La faible profondeur de l’armoire ne permet pas réellement de distinguer un point de fuite. Pourtant, une part non négligeable des élèves dessine l’armoire en utilisant un point de fuite. L’occasion nous est donc fournie de mettre en exergue une première rupture, celle entre les dessins en arts plastiques et les représentations en perspective cavalière utilisées en mathématiques.
D’ordinaire, je signifie à l’élève qu’il a effectué un dessin «  comme en arts plastiques », précisant que c’est très bien, mais que, en mathématiques, nous ne dessinons pas « comme en arts plastiques ». Et donc nous voulons qu’il essaie d’effectuer un tracé « comme en mathématiques  », ce qui parfois ne signifie rien pour l’élève ; toutefois « une seconde chance » lui est ainsi offerte.
La rupture est assez importante : c’est le moment de demander l’attention de toute la classe. Nous pouvons alors effectuer au tableau un dessin avec un point de fuite et y ajouter des représentations en perspective cavalière. On peut en profiter pour entériner l’idée que, d’une manière ou d’une autre, pour représenter un solide dans le plan, nous sommes contraints de déformer l’objet que nous représentons. Or, différentes stratégies s’offrent à nous, d’où le « comme en arts plastiques » et le « comme en mathématiques ».

 

 

 

Mise en place de la perspective cavalière « partielle ».

La dernière erreur fréquente est de dessiner avec justesse le haut de l’armoire mais pas le bas. On peut dire à l’élève que, sur son dessin, il semble que le bas de l’armoire « devant  » continue sur le bord de l’armoire, alors que dans la réalité on voit bien une face « devant » différente de la face « sur le côté  ».

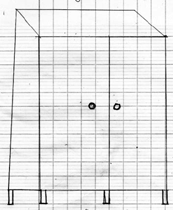
Sauf cas exceptionnel, cela suffit pour qu’il corrige son erreur.

 

 

 

 

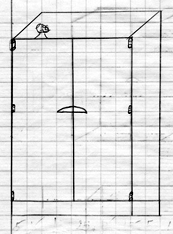
Le même genre de remarque permet de corriger les élèves dont les arêtes latérales n’ont pas exactement la même direction.

 

 

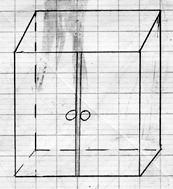
Cependant, il s’agit de rester vigilant car ce type d’erreur a tendance à réapparaître ultérieurement.

 

Prolongement pour les élèves les plus rapides

Une question récurrente nous pose souvent problème : «  Comment occuper efficacement ces élèves qui, avec une dextérité implacable, effectuent tous les tracés qu’on peut leur demander ; qui résolvent les problèmes proposés avec une virtuosité exemplaire ? Comment les faire progresser à la mesure de leurs capacités ? ». Puisqu’il n’est pas question de les laisser sombrer dans un ennui profond qui les conduirait immanquablement à des lieues du plaisir d’apprendre ou qui, pire encore, les amènerait à se faire rabrouer parce qu’ils auraient choisi de bavarder, voici deux pistes parmi d’autres.

Dessiner l’intérieur de l’armoire

Cette première piste ne les occupe pas longtemps mais les amuse assez. Ils sont des X-Men. Ils ont des pouvoirs spéciaux. Ils peuvent voir à travers les armoires. Ils doivent donc dessiner l’intérieur de l’armoire. Cependant, malgré leurs super-pouvoirs, ils ne voient pas très bien à l’intérieur des objets. Ainsi doivent-ils dessiner l’intérieur de l’armoire, d’une autre couleur ou… en pointillés.

Dessiner l’armoire portes ouvertes

 

 
Cette fois, les élèves doivent dessiner l’armoire portes ouvertes.
D’habitude les portes ne posent pas de problème aux élèves. Par contre, ils dessinent le plus souvent la tranche des étagères seulement.

 

 

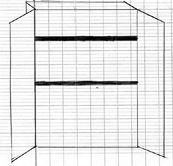
Une autre piste possible que je n’ai pas expérimentée en classe serait de demander de dessiner l’armoire en respectant les proportions, quitte à ce qu’ils puissent se lever pour prendre des mesures.

 

 

 

Prolongements pour les cours ultérieurs

On peut, par exemple, s’en tenir aux objectifs de cette activité, c’est

 distinguer les représentations avec point de fuite et les représentations en perspective cavalière ;
 savoir tracer la représentation en perspective cavalière d’un pavé droit sur papier quadrillé ou papier pointé.
Auquel cas, nous pouvons exhiber les règles de représentation en perspective cavalière et les faire noter dans le cahier de leçons.
Une autre possibilité est de reprendre l’activité sur papier blanc, ce qui ouvre de nouvelles perspectives : utilisation de l’équerre, tracé de rectangles, de droites parallèles.
Dans tous les cas, on peut espérer que cette activité ludique, durant laquelle nous n’aurons jamais dit « C’est faux !  », permettra aux élèves de débuter l’année avec une certaine confiance.

Un des points positifs, et non des moindres, de cette séance est de mettre les élèves en activité sans que leur appréhension des mathématiques ne les freine, notamment pour ceux dont la scolarité aurait déjà été douloureuse dans cette discipline. Le changement de cadre, effectuer des tracés en géométrie dans l’espace mais dans une situation concrète, peut permettre de motiver des élèves pourtant en difficulté.

Évidemment, il faudra remettre l’ouvrage sur le métier avec d’autres situations et, éventuellement, des changements de cadre pour pouvoir dépasser durablement les blocages de certains élèves devant les mathématiques.

En espérant que cette activité puisse être un premier pas efficace en la matière.

<redacteur|auteur=13>