Annales
Olympiades académiques de mathématiques
Concours national et académique, les Olympiades nationales de mathématiques ont pour objectif de développer la curiosité et l’esprit critique en confrontant les candidats à des situations de recherche individuelle ou par équipe.
Cette rubrique n’est pas à jour
par manque de volontaires pour la gérer.
Vous souhaitez participer au groupe Olympiades pour rédiger les corrections des sujets collectés et coder les documents en Latex. Nous avons besoin de vous, alors n’attendez plus n’hésitez pas à nous contacter ou à en parler autour de vous
L’A.P.M.E.P. ne cesse de préconiser que l’enseignement des mathématiques se préoccupe, avec un égal intérêt, des huit moments d’une véritable formation scientifique :
- poser un problème,
- expérimenter, prendre des exemples,
- conjecturer,
- se documenter,
- bâtir une démonstration,
- mettre en œuvre des outils adéquats,
- évaluer la pertinence des résultats,
- communiquer.
Voux trouverez tous renseignements, calendrier et organisations, sur le site de nos Olympiades françaises, au souci non élitiste bien marqué désormais, par une ouverture accrue aux diverses séries, et qui peuvent s’insérer dans ce type de formation… D’autant qu’il y a lieu d’éviter la regrettable dichotomie qui pourrait s’instaurer entre de « ludiques » activités de clubs mathématiques et « d’austères » heures classiques de mathématiques.
Par leur nature nos Olympiades évitent cet écueil. Elles peuvent, au contraire, irriguer tout notre enseignement. Tel est, pour l’APMEP, leur intérêt majeur.
- Les Olympiades nationales de mathématiques
de Karim Zayana
Cet article, paru dans le Bulletin Vert n°524, donne des conseils pour comprendre et réussir les épreuves.
Une erreur, une coquille, un problème, une envie de coder, une envie de faire une documentation, ou de contribuer aux solutions, n’hésitez pas à nous contacter
- Olympiades académiques 2020
- Olympiades académiques 2019
- Olympiades académiques de 2001 à 2018
- Brochures des Olympiades académiques
 Olympiades 2020
Olympiades 2020
Énoncés et Solutionsolympiades académiques
de mathématiques.
 Olympiades 2019
Olympiades 2019
Énoncés et Solutionsolympiades académiques
de mathématiques.
 Brochures des olympiades académiques
Brochures des olympiades académiques
Les brochures APMEP
des olympiades académiques
de mathématiques
de 2001 à 2018.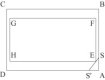 CAEN - Exercice n° 2
CAEN - Exercice n° 2
GEOMETRIE PLANE - Série S
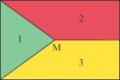 CAEN - Exercice n° 1
CAEN - Exercice n° 1
Série S - Géométrie plane
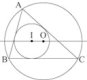 BORDEAUX - Exercice n° 1
BORDEAUX - Exercice n° 1
Série S - Géométrie plane
BESANCON - Exercice n° 2 Section S - DENOMBREMENT
BESANCON - Exercice n° 1 Série S - Arithmétique
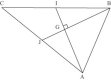 AMIENS - Exercice n° 4
AMIENS - Exercice n° 4
Sections STI-STL - Géométrie plane
AMIENS - Exercice n° 2 Série S - Géométrie plane
AMIENS - Exercice n° 3 Séries concernées : STI - STL
Équations - Fonctions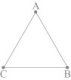 AMIENS - Exercice n° 1
AMIENS - Exercice n° 1
Série S - Arithmétique - Géométrie plane.
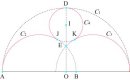 AIX-MARSEILLE - Exercice n° 2
AIX-MARSEILLE - Exercice n° 2
Aix Marseille - N° 2 - Série S
AIX-MARSEILLE — Exercice n° 1 Aix-Marseille - n° 1 - Série S
Sujet national n° 2 Sujet national toutes séries numéro 2 (Géométrie plane)
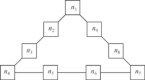 Sujet National n° 1
Sujet National n° 1
Toutes séries - Arithmétique
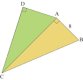 AIX-MARSEILLE - Exercice n° 3
AIX-MARSEILLE - Exercice n° 3
Thème : arithmétique. Série concernée : S
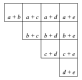 Limoges : sujet 2
Limoges : sujet 2
Thème : Arithmétique, numération