Les Problèmes de l’APMEP
Les problèmes n° 303 et 304 Indications sur des énoncés déjà publiés
Énoncé 300 (si $\sum a(d) = 2^n , a(n)$ est divisible par $n$) : Soit $p$ un facteur premier de $n$…
Énoncé 301 ($f (\alpha) f(\beta) f(\gamma) = f (\alpha) + f (\beta) + f (\gamma)$ si $ \alpha+\beta +\gamma=\pi$) : Utilisons la fonction tangente...
Énoncé 302 (101 pièces … toutes de même masse ?) : Quel est le rang de la matrice ?
Énoncés des nouveaux problèmes
Énoncé n°303 (R. FERACHOGLOU et M. LAFOND, 21-Dijon) Soit (Q) un quadrilatère plan convexe, (...) Problèmes n°305 et 306
Problèmes n°305 et 306
Indications sur des énoncés déjà publiés Énoncé 303 (médianes d’un quadrilatère : 5 ≤ aire(Q) /aire(q) < 6) :
Le rapport vaut 5 si le petit quadrilatère q est un trapèze, il tend vers 6 si Q et q tendent vers des triangles.
Énoncé 304 ($ 2x^2 + 1 = y^ n $) :
Peut-on factoriser le premier membre ?
Énoncés des nouveaux problèmes Énoncé n°305 (Pierre DUCHET, 75-Paris) En appelant « sphinx » et « parallélogramme » les deux formes que voici : a) Peut-on paver complètement un triangle équilatéral, de côté (...)Les problèmes du bulletin vert Solutions des problèmes antérieurs
Problème n°280 (Dominique ROUX, 87 - Limoges) Soit S l’ensemble des entiers k ≥ 2 tels qu’il existe k entiers consécutifs, (n + 1),
(n + 2), ..., (n + k), n ≥ 0, dont la somme des carrés soit un carré parfait :
$$(n + 1)^2 + (n + 2)^2 + … + (n + k)^2 = m^2$$
a) Montrer que l’ensemble S est infini, et qu’il existe une infinité d’entiers qui n’appartiennent pas à S b) Montrer qu’il existe des entiers k ∈ S tels que l’équation :
$$(n + 1)^2 + (n + 2)^2 (...)Les problèmes du bulletin vert Solutions des problèmes antérieurs Problème n°280 (Dominique ROUX, 87 - Limoges) Soit S l’ensemble des entiers k ≥ 2 tels qu’il existe k entiers consécutifs, (n + 1), (n + 2), ..., (n + k), n ≥ 0, dont la somme des carrés soit un carré parfait : $$(n + 1)^2 + (n + 2)^2 + … + (n + k)^2 = m^2$$ a) Montrer que l’ensemble S est infini, et qu’il existe une infinité d’entiers qui n’appartiennent pas à S b) Montrer qu’il existe des entiers k ∈ S tels que l’équation : $$(n + 1)^2 + (n + 2)^2 + … + (...)
Les problèmes du bulletin vert Solutions des problèmes antérieurs
Problème n°281 (Moubinool OMARJEE, 75 - Paris) Soit une série convergente, de terme général \(\alpha_n\), de somme S. Montrer qu’il existe une suite croissante \((k_n)\) d’entiers naturels, qui tende vers l’infini lorsque n tend vers l’infini, et telle que la série de terme général \(k_n\alpha_n\) soit convergente.
SOLUTION
Problème n°282 (Raymond PRUDHOMME, 76 - lsneauville) Soit ABC un triangle et ( Γ ) son cercle circonscrit. Les bissectrices (...)Les problèmes n°293 et 294 Énoncés des nouveaux problèmes
Problème n°293 (Pierre BORNSZTEIN, 95 - Pontoise) Initialement, n oiseaux se trouvent chacun à un sommet d’un polygone régulier à n côtés. Lorsqu’ils sont apeurés, ces oiseaux s’envolent. Puis, après quelque temps, ils reviennent se poser un sur chaque sommet du polygone, mais pas nécessairement sur leurs positions initiales. Trouver tous les n > 0 pour lesquels il existe nécessairement trois oiseaux qui, avant et après l’envol, forment deux triangles tous deux (...)Les problèmes n° 295 et 296 Énoncés des nouveaux problèmes
Problème n°295 (Michel LAFOND, 21-Dijon) Démontrer que le nombre de triangles inégaux de périmètre n à côtés entiers et non aplatis est égal au nombre de manières de payer (n − 3) euros avec des pièces de 2, 3 ou 4 euros.
voir l’article où est publiée une solution
Problème n°296 (Raymond RAYNAUD, 04-Digne) Les parallèles à une droite (d) menées par les sommets d’un triangle ABC recoupent respectivement son cercle circonscrit en A′ , B′ , C′. P étant un (...)Problèmes n° 307, 308, 309 François LO JACOMO Indications sur des énoncés déjà publiés Énoncé n°305 (pavage par des sphinx ou des parallélogrammes) : a) seuls sont pavables par des sphinx les triangles de côté multiple de 12. b) dans un hexagone de côté 3, on peut mettre au plus 12 parallélogrammes.
Énoncé n°306 (une caractérisation des droites de Simson) : Quelle méthode recommander ? que les droites de Simson relatives à ABC sont les asymptotes des hyperboles équilatères passant par A, B et C ?
Énoncés des nouveaux problèmes (...)Les problèmes du bulletin vert Solutions des problèmes antérieurs
Problème 287 (Pierre SAMUEL, 92-Bourg la Reine) À tout polynôme \(P(w) = aw^2 + 2bw + c \ \ \ (a, b, c \in \mathbb Z, a > 0, 0 ≤ b < a)\) on associe
l’équation : \(x^2 − ay^2 = b^2 − ac\).
1 – Toute équation (E) : \(x^2 − ay^2 = k \ \ \ (a, k \in \mathbb Z, a > 0)\) est-elle associée à des polynômes P(w) et à combien (commencer par le cas où a est premier avec k) ?
2 – Quelles relations y a-t-il entre les solutions entières (x, y) de (E) et les valeurs (...)Les problèmes du bulletin vert Solutions des problèmes antérieurs
Problème 288 (Philippe DELEHAM, 97-Ouangani)
Deux cercles \((C_1)\) et \((C_2)\) se coupent en A et B. La tangente à \((C_1)\) en A coupe \((C_2)\) en C. La tangente à \((C_2)\) en B coupe \((C_1)\) en D. La droite (CD) coupe \((C_1)\) en E et \((C_2)\) en F. Montrer que
$$\frac1FB^2+\frac1BD^2+\frac1DA^2=\frac1EA^2+\frac1AC^2+\frac1CB^2$$
Télécharger la solution (...)Les problèmes n°297 et 298 Énoncés des nouveaux problèmes
Problème n°297 (Jacques BOUTELOUP, 76-Rouen) On considère quatre cercles du plan tangents deux à deux en des points distincts. 1) Démontrer que trois d’entre eux sont tangents extérieurement deux à deux, le quatrième étant soit tangent extérieurement, soit tangent intérieurement à chacun des trois autres. 2) On désigne par $z_i$ les affixes des centres dans une représentation complexe du plan euclidien, par $r_i$ leurs rayons et l’on pose $c_i= - \frac1r_i$ (...)Les problèmes du BV 512 Énoncés des nouveaux problèmes
Problème 512-1 (Michel Lafond (Dijon)) Le nombre N ! écrit en base dix se termine par un huit suivi d’exactement mille zéros. Que vaut N ?
voir l’article où est publiée une solution
Problème 512-2 Dans le probleme 21 posé dans un bulletin vert en 2006, on démontre que les solutions rationnelles de l’équation $x^y = y^x$ avec x < y sont données par $$x=\left(\fracn+1n\right)^n \text et y=\left(\fracn+1n\right)^n+1$$ avec n $\in \mathbb N$. On pose (...)Les problèmes n°310 et 311 Indications sur des énoncés déjà publiés
Énoncé 307 (peser avec une balance Roberval) : 3 poids suffisent pour M = 13 (on rappelle que les poids peuvent être placés sur les deux plateaux de la balance).
Énoncé 308 (composé de rotations axiales d’un tiers ou quart de tour) : Que peut-on dire des grandes diagonales d’un cube ?
Énoncé 309 (triangle dont l’orthocentre est centre du cercle inscrit de ABC) : Ce même point est l’orthocentre d’un autre triangle et le centre d’une similitude (...)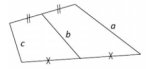 Les problèmes du BV 511
Les problèmes du BV 511
Énoncés des nouveaux problèmes
Problème 511-1 Trouver tous les polynômes scindés sur $\mathbb R$ et à coefficients dans $\–1,0,1\$.
Problème 511–2 (Michel Lafond (Dijon)) Soit Q un quadrilatere convexe non aplati. Deux côtes opposés de Q mesurent a et c. La médiane joignant les milieux des deux autres côtés mesure b. Démontrer que si $b^2=\fraca^23+c^2$, alors Q est un trapèze.
Problème 511–3 Une application f : $\mathbb R \rightarrow \mathbb R$ transformant tout segment en segment est-elle (...)Les problèmes du BV 510 Énoncés des nouveaux problèmes
Problème 510-1 (Michel Bataille, Rouen) Soit ABC un triangle rectangle en A, non isocèle. Trouver la valeur minimale de PA lorsque P est un point intérieur au triangle tel que $$\fracPA\sin \alpha=\frac12\sqrt\fracPB\sin \beta \fracPC\sin \gamma $$
où $$\alpha=\widehatBPC, \beta=\widehatCPA, \gamma=\widehatAPB$$
voir l’article où est publiée une solution
Problème 510-2 Soit $n \in \mathbb N^*$. On se donne n réels $x_1, …, x_n$, tous distincts. Montrer que pour tout (...)Les problèmes n°312 et 313 Indications sur des énoncés déjà publiés Énoncé n° 310 (entiers magiques) : Que pourrait valoir $c$ pour $n = 7$ ? Énoncé n° 311 (ex-voto japonais) : Que peut-on dire de $ tan(\frac\widehatOA_iA_i+12$) ?
Énoncés des nouveaux problèmes
Enoncé n° 312 (Pierre JULLIEN, 13-Meyreuil) Soit dans le plan quatre points A, B, C et D tels que AB = CD (égalités de longueurs). On note M le milieu de [AD] et N le milieu de [BC]. Montrer que la droite (MN) coupe les droites (AB) et (CD) sous le même angle. voir le BV où (...)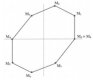 Les problèmes du BV 509
Les problèmes du BV 509
Énoncés des nouveaux problèmes
Problème 509-1 Soit f,g : $\mathbb R^*_+ \rightarrow \mathbb R$ deux fonctions intégrables sur $\mathbb R^*_+$. Montrer que la fonction $$(x,y) \mapsto \fracf(x)g(x)x+y$$ est intégrable sur $\mathbb R^*_+ \times \mathbb R^*_+$ et trouver la meilleure constante C>0 telle que $$ \left | \iint_]0,+\infty[ \times ]0,+\infty \fracf(x)g(x)x+y dxdy \right 0,+\infty[ f(x)^2 dx\sqrt\int_]0,+\infty[ g(y)^2 dy$$
voir l’article où est publiée une solution
Problème 509–2 (...)Les problèmes du BV 508 Énoncés des nouveaux problèmes
Problème 508-1 On considère une application f : $\mathbb R \rightarrow \mathbb R$ qui envoie tout segment de $\mathbb R$ sur un segment de même longueur. Trouver f.
voir l’article où est publiée une solution
Problème 508-2 (Isao Sauzzede, élève en MP à Clermont-Ferrand) Soit $E = \mathcal C$ ([0 ; 1], $\mathbb R$ ) l’ensemble des applications réelles continues sur [0,1]. On définit une application $\tau$ : $E \rightarrow E$ de la façon suivante : pour $f \in E$, $$ \tau (...)