Dans nos classes
 À table !
À table !
Cet article, terminé le jour de son anniversaire, est dédié à ma filleule Agnès trop tôt arrachée à notre affection peu après son succès au Capes de maths.
La revue MATHS-JEUNES de la S.B.P.M.ef a proposé dans son numéro 115 de janvier 2002 le problème suivant appuyé sur la figure 1 ci-jointe :
Déterminer les sets identiques pour qu’ainsi disposés sur une table circulaire ils la recouvrent au maximum. En son numéro 117 d’avril 2007, MATHSJEUNES propose une solution algébrique :
avec \(AB= l \over 2\) et (...) Le problème de Tammes
Le problème de Tammes
1. Origine
1.1. Un problème de botanique
Le botaniste hollandais Tammes découvrit, en étudiant les grains de pollen, que ces grains, approximativement sphériques, portent des orifices dont la répartition présente une certaine régularité, en ce sens qu’ils semblent aussi éloignés que possible les uns des autres.
Dans l’article, daté de 1930, où il rendait compte de cette trouvaille, il s’interrogeait sur ce qui fut très vite appelé le « problème de Tammes » : Comment répartir n points sur une sphère de (...)Nombres rimant avec leur carré Julien Moreau
Le carré d’un entier finissant par 6 finit par 6 ; le carré d’un entier finissant par 76 finit par 76, celui d’un entier finissant par 376 finit par 376. Peut-on continuer ainsi indéfiniment ? Et, plus généralement, comment fabriquer des nombres dont le carré rime riche, si l’on peut dire, avec le nombre lui-même ?
Ce problème n’a qu’un intérêt anecdotique [1], mais il est assez distrayant et constitue un bon thème de travail sur la divisibilité et les congruences dans l’enseignement de (...) MÉDÉE : Une méthode pour construire des algorithmes
MÉDÉE : Une méthode pour construire des algorithmes
Nous allons exposer, étape par étape, le principe d’une méthode d’analyse appelée
méthode déductive, médée en abrégé. Médée a été largement utilisé dans le cadre de
l’enseignement de l’Option Informatique dans les années 80. La méthode est générale
et peut être utilisée pour toutes les constructions d’algorithmes. Elle est issue des
travaux de Claude Pair sur la construction systématique des programmes menés au CRIN de Nancy. Méthode
Marche rationnelle de l’esprit pour arriver à la connaissance ou à la (...)Les figures : papier ou écran ? Le texte qui précède a été écrit par Henri Bareil il y a vingt et un ans. À l’époque Cabri Géomètre n’existait que depuis deux ans, et l’équipement informatique des lycées comme des familles était fort limité. Depuis, la disponibilité de logiciels de géométrie dynamique s’est largement accrue, avec la création de Geoplan en 1996 (et Geospace peu après) et la floraison, au XXIe siècle, de logiciels gratuits : GeoGebra, CarMetal, XCas, MathGraph, … ainsi que la version gratuite de Geoplan et Geospace. Maintenant (...)
 Parties carrées à l’école élémentaire !
Parties carrées à l’école élémentaire !
Daniel Djament IUFM de l’académie de Créteil, université Paris 12.
Rassurez-vous, derrière ce titre égrillard se cache un honnête problème de mathématiques pour de jeunes élèves. Supposons que l’on dispose d’un carré et d’une paire de ciseaux et que l’on veuille découper ce carré en parties carrées. Il revient au même de tracer une partition du carré initial en parties toutes carrées.
Voyons quelques exemples de partitions, on peut facilement couper en 4, en 7, en 9 :
Il est tentant de se poser la (...) Rôle des figures à propos du raisonnement
Rôle des figures à propos du raisonnement
1. Du particulier à l’universel
Les problèmes de géométrie conduisent à établir des propriétés vraies pour tel ou tel type de configuration ? Or les libellés scolaires classiques peuvent masquer cette recherche d’universalité ? Voici par exemple le problème : « dessiner un quadrilatère ; étudier la configuration des milieux des cotés. » L’étude demandée conduit implicitement à établir une propriété vraie pour tout quadrilatère de départ alors qu’il n’y a qu’un et un seul quadrilatère dessiné. Mais comment un (...) Orthocentre, cercle d’Euler et hyperbole équilatère
Orthocentre, cercle d’Euler et hyperbole équilatère
L’étude géométrique est de J.-P. Friedelmeyer, l’adaptation au niveau lycée et les activités GeoGebra sont de Marc Roux. Les fichiers GeoGebra sont sur le site de l’APMEP, rubrique Publications, Bulletin Vert, Sommaires
Le premier et le dernier des trois objets énumérés dans le titre de cet article sont bien connus individuellement des élèves de lycée, et leurs professeurs connaissent aussi le cercle d’Euler. Ce qui est moins classique, c’est leur remarquable conjugaison dans quelques belles propriétés (...) Le calcul réfléchi : entre sens et technique
Le calcul réfléchi : entre sens et technique
Résumé : Depuis quelques années, au niveau de l’école primaire et du collège, il apparaît, dans les discours institutionnels, une incitation à faire des activités rituelles et notamment ce qu’on désigne par calcul mental ou calcul réfléchi. Dans cet article, nous souhaitons initier une réflexion sur ce point et proposer des idées aux professeurs de collège pour mettre en oeuvre des activités rituelles de calcul réfléchi intégrées aux progressions et au travail fait dans les autres chapitres, notamment ceux de calcul littéral ou équations (inéquations). De plus, nous voulons présenter comment ces activités dites rituelles peuvent être intégrées dans les progressions de chaque classe et permettre d’anticiper sur les notions enseignées.
 Compter nos ancêtres en base 2
Compter nos ancêtres en base 2
De nos jours, quiconque entend parler de numération binaire pense aussitôt à l’informatique. Et pourtant, depuis plusieurs siècles, les généalogistes professionnels et amateurs ont adopté un codage qui est implicitement binaire.
L’idée remonte à l’allemand Michael Eytzinger (1590) ; elle a été reprise en 1676 par Jeronimo de Sosa, franciscain espagnol, dans sa Noticia de la gran casa de los marqueses de Villafranca et popularisée par Stefan Kekule von Stradonitz dans son Ahnentafelatlas (Atlas des (...)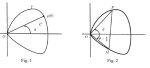 Des démonstrations qui font boum !
Des démonstrations qui font boum !
Lorsqu’en cours, à la fin de la démonstration d’un résultat, je m’exclame « Voilà une démonstration qui fait boum ! », mes étudiants savent qu’il s’agit d’une démonstration particulièrement courte et astucieuse, qui mérite d’être relue et étudiée à tête reposée... Mais qu’est-ce qu’une démonstration qui fait boum ? Je vais essayer de l’illustrer dans cette note avec trois exemples.
Avant cela, prenons le temps de quelques réflexions. Un énoncé de mathématiques n’a de valeur que s’il est démontré ... chose qu’il est (...) Les triplets pythagoriciens : une source d’exercices et problèmes au lycée et au collège ?
Les triplets pythagoriciens : une source d’exercices et problèmes au lycée et au collège ?
Introduction
Dans les « Nouveaux éléments de géométrie » d’Antoine Arnauld, édition de 1683, on lit : « Tout nombre composé de deux carrés, comme 4 + 1 (5), 9 + 4 (13), 16 + 1 (17), 16 + 9 (25), a son carré égal à deux carrés. Et il n’y a que ces nombres-là, ou leurs multiples, qui aient cette propriété ». Il est clair qu’il faut entendre carrés non nuls, car pour tout $n, n^2 = n^2 + 0^2$. Je désignerai par (P1) la première de ces deux affirmations, par (P2) la deuxième. (P1) n’est pas exacte si l’on ne (...) Le paraboloïde hyperbolique d’équation \(z = xy\)
Le paraboloïde hyperbolique d’équation \(z = xy\)
Jacques Lucet
Lycée Jean-Baptiste de la Salle à Saint-Denis (93). jacques.lucet@laposte.net De l’architecture aux mathématiques : des lycéens sur le terrain
De l’architecture aux mathématiques : des lycéens sur le terrain
Odile Jenvrin, Lycée Lemonnier, Caen et IREM de Basse-Normandie.
 Problèmes ouverts pour l’école élémentaire.
Problèmes ouverts pour l’école élémentaire.
Dans le bulletin no 418 de septembre-octobre 1998, la Commission Premier Degré proposait une rubrique réunissant des énoncés de problèmes « qu’on n’a pas encore appris à résoudre » pour des élèves de l’école élémentaire. Voici quelques énoncés supplémentaires.
Messages à ceux qui utiliseront ces problèmes dans une classe : La Commission aimerait recevoir quelques renseignements ou comptes rendus des expérimentations. D’autre part, elle ne possède pas une collection illimitée de tels problèmes. Toute (...)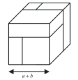 Fractions et pourcentages
Fractions et pourcentages
avec le « puzzle de Cardan »François Drouin [1] La fiche–élève
Voici les cinq étapes de la construction d’un puzzle de Cardan. Un cube 3 × 3 × 3 se construit petit à petit. Numéro de l’étape 1 2 3 4 5 Nombre de cubes placés Fraction du cube 3 × 3 × 3 déjà construiteDifférencier une suite aléatoire d’une autre qui ne l’est pas. Jean François Kentzel [1]
Une version plus détaillée de cet article est sur le site du lycée
Pardailhanà Auch (32) où j’enseigne, site désigné par PARD dans ce qui suit. Résumé de l’article
Cet article est le récit détaillé de deux séances en classe de première : description des activités et commentaires.
L’idée est de comparer des listes de nombres, les unes inventées, les autres obtenues par la touche simulation de la calculatrice, puis comptage des « inversions », et des suites de nombres « sans inversion (...) Ovale, bel ovale
Ovale, bel ovale
À Henri.
Le souvenir de son amitié
et de son charisme nous restera,
mais ses conseils si pertinents
nous manquent déjà.
Figure 1
Rien ne ressemble autant à une ellipse que les formes ovales qu’utilisent les encadreurs ou les peintres (fig. 1), mais aussi les jardiniers, les architectes, les maçons, les ferblantiers et bien d’autres corps de métier. Or dans la plupart des cas ces ovales sont construits comme raccordement de quatre arcs de cercle, (...)